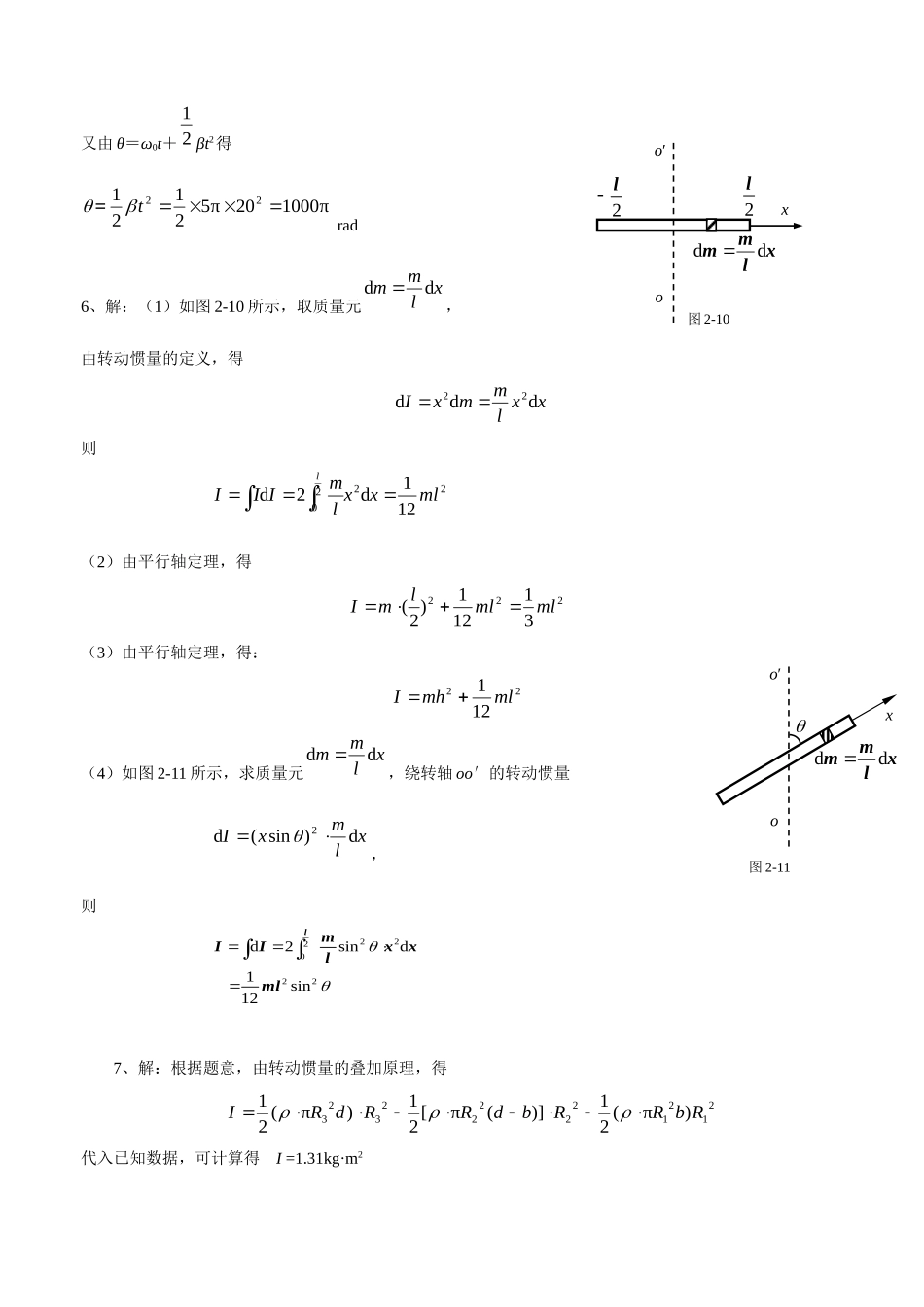
第二章刚体的转动习题1、两个半径相同的飞轮用一皮带相连,作无滑动转动时,大飞轮边缘上各点的线速度的大小是否与小飞轮边缘上各点的线速度的大小相同?角速度又是否相同?2、当刚体转动时,如果它的角速度很大,是否说明刚体的角加速度一定很大?3、如果作用在刚体上的合力矩垂直于刚体的角动量,则刚体角动量的大小和方向会发生变化吗?4、一个人随着转台转动,两手各拿一只重量相等的哑铃,当他将两臂伸开,他和转台的转动角速度是否改变?5、直径为0.6m的转轮,从静止开始做匀变速转动,经20s后,它的角速度达到100πrad/s,求角加速度和在这一段时间内转轮转过的角度。6、求质量为m,长为l的均匀细棒对下面几种情况的转动惯量。(1)转轴通过棒的中心并与棒成垂直;(2)转轴通过棒的一端并与棒垂直;(3)转轴通过棒上离中心为h的一点并与棒成垂直;(4)转轴通过棒中心并和棒成θ角。7、如图2-19所示,一铁制飞轮,已知密度ρ=7.8g/cm3,R1=0.030m,R2=0.12m,R3=0.19m,b=0.040m,d=0.090m,求它对转轴的转动惯量。8、一飞轮直径为0.3m,质量为5kg,边缘绕绳,现用恒力拉绳一端,使它由静止均匀地加速,经0.5s转速达到10rev/s,假定飞轮可看做实心圆柱体,试求:(1)飞轮的角加速度及其在这段时间内转过的转数;(2)从拉动后t=10s时飞轮的角速度及轮边缘上一点的速度和加速度。(3)拉力及拉力所作的功;9、用线绕于半径R=1m,质量m=100kg的圆盘上,在绳的一端作用10N的拉力,设圆盘可绕过盘心垂直于盘面的定轴转动。试求:(1)圆盘的角加速度;(2)当线拉下5m时,圆盘所得到的动能。10、两个质量为m1和m2的物质分别系在两条绳上,这两条绳又分别绕在半径为r1和r2并装在同一轴的两鼓轮上,如图2-20所示。已知两鼓轮绕轴的转动惯量为I,轴间摩擦不计,绳子的质量忽略不计,求鼓轮的角加速度。11、如图2-21所示,已知滑轮的半径为30cm,转动惯量为0.50kg·m2,弹R1R2R3db图2-19m1m2r2r1O图2-20图2-21簧的劲度系数k=2.0N/m。问质量为60g的物体落下40cm时的速率是多大?(设开始时物体静止且弹簧无伸长,在物体下落过程中绳子与滑轮无相对滑动)。12、如图2-22所示,一不变的力矩M作用在铰车的鼓轮上使轮转动。轮的半径为r,质量为m1,缠在鼓轮上的绳子系一质量为m2的重物,使其沿倾角为θ的斜面滑动,重物和斜面之间的滑动摩擦系数为μ,绳子的质量忽略不计,鼓轮可看作均质实心圆柱,在开始时此系统静止,试求鼓轮转过角φ时的角速度。13、一转台绕竖直轴转动,每10s转一周,转台对轴的转动惯量为1200kg·m2.。质量为80kg的人,开始站在台的中心,随后沿半径向外跑去,问当人离转台中心2m时,转台的角速度是多少。14、有圆盘A和B,盘B静止,盘A的转动惯量为盘B的一半。它们的轴由离合器控制,开始时,盘A、B是分开的,盘A的角速度为ω0,两者衔接到一起后,产生了2000J的热,求原来盘A的动能为多少?15、一根质量为m,长为l的均匀细棒,绕一水平光滑转轴O在竖直平面内转动。O轴离A端距离为3l,此时的转动惯量为91ml2,今使棒从静止开始由水平位置绕O轴转动,试求:(1)棒在水平位置上刚起动时的的角加速度;(2)棒转到竖直位置时角速度和角加速度;(3)转到垂直位置时,在A端的速度及加速度。(重力作用点集中于距支点6l处)参考答案1、答:由于大小飞轮用一根皮带相连,且作无滑动转动,所以大小飞轮边缘上各点的线速度大小相等;但由于大小飞轮边缘半径不同,小飞轮的角速度要比大飞轮的角速度要大。2、答:刚体转动时,角速度很大,不能说明刚体的角加速度一定很大,因为角加速度越大的刚体,仅表明角速度的变化越快。3、答:作用在刚体上的合力矩垂直于刚体的角动量,则该力矩不改变角动量的大小,仅仅改变其方向。4、答:当人的两臂伸开时,其绕轴转动的转动惯量增大,根据角动量守恒定律,人和转台的转动角速度必将减少。5、解:转轮做匀变速转动,由ω=ω0+βt得π520π100t=rad/s2Mm1m2θ图2-22又由θ=ω0t+21βt2得π100020π5212122t=rad6、解:(1)如图2-10所示,取质量元xlmmdd,由转动惯量的定义,得xxlmmxIddd22则2220...