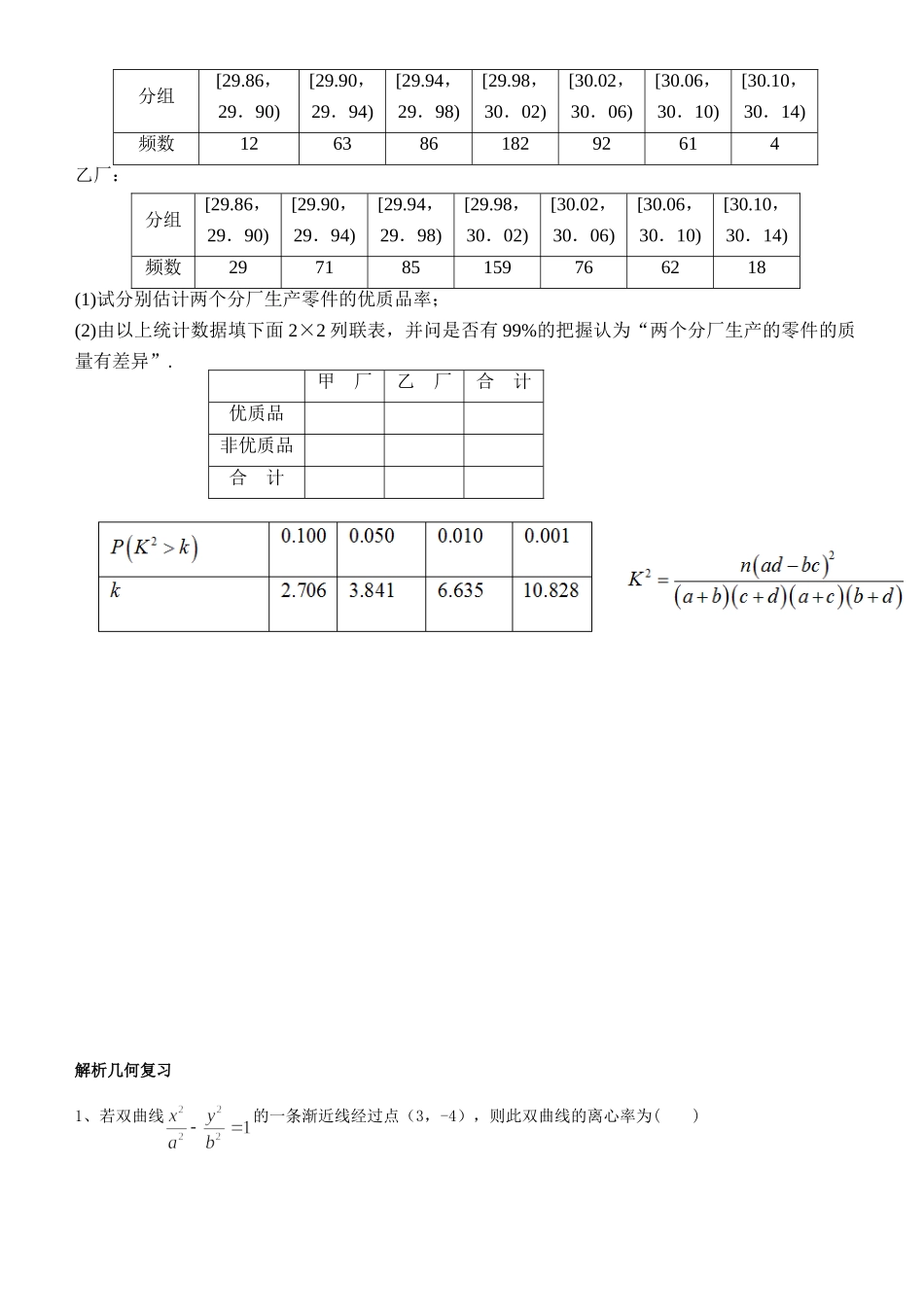
变量间的相关关系与统计案例基础梳理1．相关关系的分类从散点图上看，点散布在从左下角到右上角的区域内，对于两个变量的这种相关关系，我们将它称为正相关；点散布在从左上角到右下角的区域内，两个变量的这种相关关系称为负相关．2．线性相关从散点图上看，如果这些点从整体上看大致分布在一条直线附近，则称这两个变量之间具有线性相关关系，这条直线叫回归直线．3．回归方程(1)最小二乘法：使得样本数据的点到回归直线的距离平方和最小的方法叫最小二乘法．(2)回归方程：两个具有线性相关关系的变量的一组数据：(x1，y1)，(x2，y2)，…，(xn，yn)，其回归方程为y＝bx＋a，则，其中，b是回归方程的斜率，a是在y轴上的截距．4．样本相关系数，用它来衡量两个变量间的线性相关关系(1)当r＞0时，表明两个变量正相关；(2)当r＜0时，表明两个变量负相关；(3)r的绝对值越接近1，表明两个变量的线性相关性越强；r的绝对值越接近于0，表明两个变量之间几乎不存在线性相关关系．通常当|r|＞0
75时，认为两个变量有很强的线性相关关系．5．线性回归模型(1)y＝bx＋a＋e中，a、b称为模型的未知参数；e称为随机误差．(2)相关指数用相关指数R2来刻画回归的效果，其计算公式是：R2＝，R2的值越大，说明残差平方和越小，也就是说模型的拟合效果越好．在线性回归模型中，R2表示解释变量对预报变量变化的贡献率，R2越接近于1，表示回归效果越好．6．独立性检验(1)用变量的不同“值”表示个体所属的不同类别，这种变量称为分类变量．例如：是否吸烟，宗教信仰，国籍等．(2)列出的两个分类变量的频数表，称为列联表．(3)一般地，假设有两个分类变量X和Y，它们的值域分别为{x1，x2}和{y1，y2}，其样本频数列联表(称为2×2列联表)为：2×2列联表y1y2总计x1aba＋bx2cdc＋d总计a＋cb＋da＋b＋c＋
