反三角函数与简单三角方程VIP免费

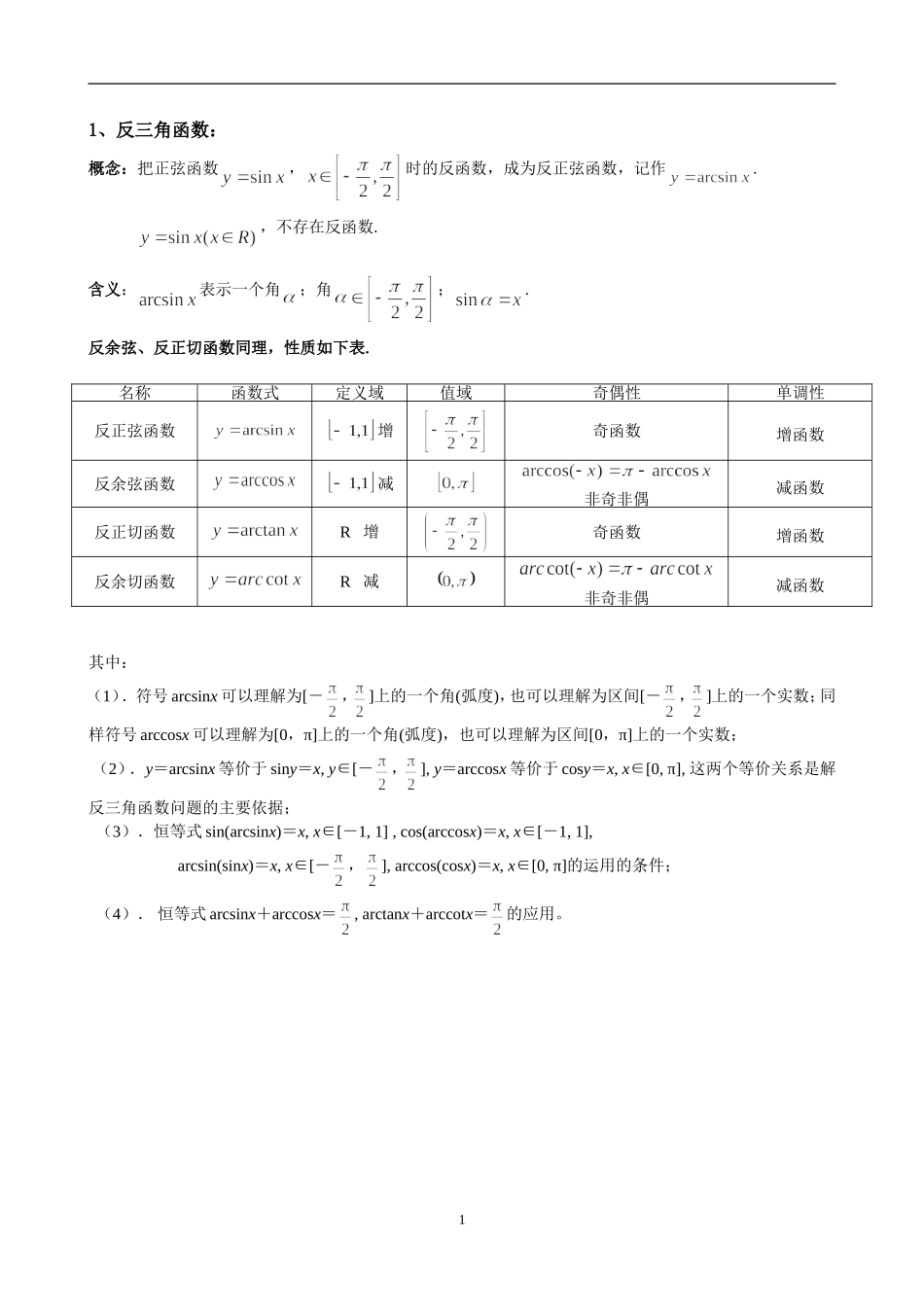
1、反三角函数：概念：把正弦函数，时的反函数，成为反正弦函数，记作.，不存在反函数.含义：表示一个角；角；.反余弦、反正切函数同理，性质如下表.其中：（1）．符号arcsinx可以理解为[－，]上的一个角(弧度)，也可以理解为区间[－，]上的一个实数；同样符号arccosx可以理解为[0，π]上的一个角(弧度)，也可以理解为区间[0，π]上的一个实数；（2）．y＝arcsinx等价于siny＝x,y∈[－，],y＝arccosx等价于cosy＝x,x∈[0,π],这两个等价关系是解反三角函数问题的主要依据；（3）．恒等式sin(arcsinx)＝x,x∈[－1,1],cos(arccosx)＝x,x∈[－1,1],arcsin(sinx)＝x,x∈[－，],arccos(cosx)＝x,x∈[0,π]的运用的条件；（4）．恒等式arcsinx＋arccosx＝,arctanx＋arccotx＝的应用。名称函数式定义域值域奇偶性单调性反正弦函数增奇函数增函数反余弦函数减非奇非偶减函数反正切函数R增奇函数增函数反余切函数R减非奇非偶减函数12、最简单的三角方程方程方程的解集其中：（1）．含有未知数的三角函数的方程叫做三角方程。解三角方程就是确定三角方程是否有解，如果有解，求出三角方程的解集；（2）．解最简单的三角方程是解简单的三角方程的基础，要在理解三角方程的基础上，熟练地写出最简单的三角方程的解；（3）．要熟悉同名三角函数相等时角度之间的关系在解三角方程中的作用；如：若，则；若，则；若，则；若，则；（4）．会用数形结合的思想和函数思想进行含有参数的三角方程的解的情况和讨论。【例题精讲】例1.函数，，的反函数为（）yxxsin232Ayxx.arcsin，，11Byxx.arcsin，，11Cyxx.arcsin，，11Dyxx.arcsin，，11分析与解：232xxx22，，需把角转化至主值区间。22xxxy，又sin()sin由反正弦函数定义，得xyarcsinxyyarcsin，又由已知得11所求反函数为，，yxxarcsin11例4.函数，，的图象为（）yxxarccos(cos)222分析与解：解析式可化简为，，，，yxxxxxarccos(cos)0220即，，，，显然其图象应为（）yxxxxA0220例5.函数，，的值域为（）yxxarccos(sin)()323AB..656056，，CD..323623，，分析与解：欲求函数值域，需先求，，的值域。uxxsin()323323321321xxu，，即sin而在，上为减函数yuarccos11arccos()arccosarccos321u即，故选（）056yB例6.使成立的x的取值范围是()AB..022221，，CD..12210，，分析与解：该题研究不等关系，故需利用函数的单调性进行转化，又因为求x的取值范围，故需把x从反三角函数式中分离出来，为此只需对arcsinx，arccosx同时取某一三角函数即可，不妨选用正弦函数。若，则，，而，xxx0202arcsinarccos此时不成立，故arcsinarccosxxx03若，则，，，xxx00202arcsinarccos而在区间，上为增函数yxsin02又arcsinarccossin(arcsin)sin(arccos)xxxx即，解不等式，得xxx1222||又，故选（）01221xxB例7.若，则（）022arcsincos()arccossin()ABCD....222222分析与解：这是三角函数的反三角运算，其方法是把角化到相应的反三角函数的值域内。arcsincos()arcsin(sin)arcsin(sin)2arccossin()arccos(sin)arccos(sin)arccoscos()(),222原式，故选（）()()22A例8.求值：(1)(2)分析：arcsin()arcsin()sin352235表示，上的角，若设，...