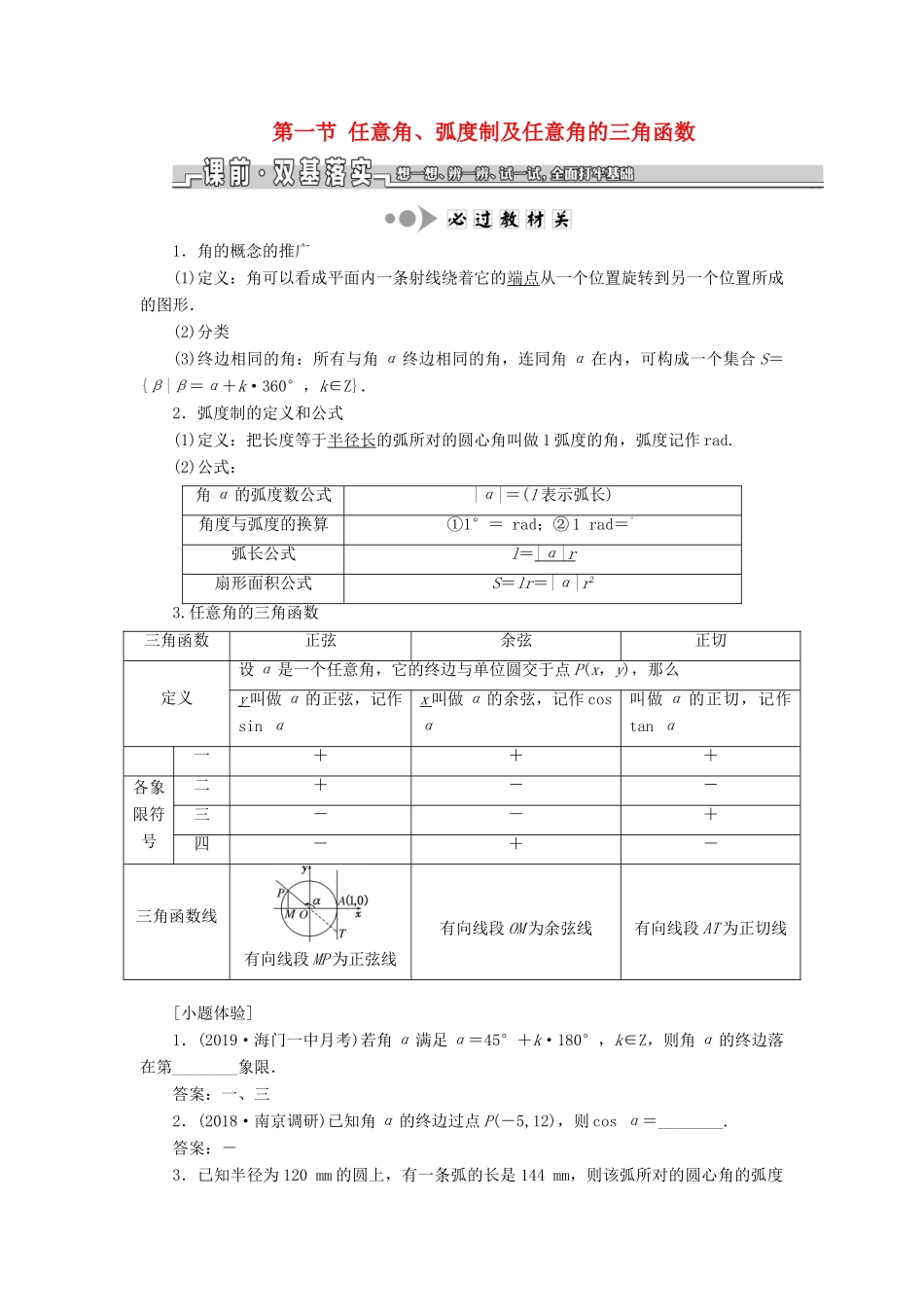
第一节任意角、弧度制及任意角的三角函数1.角的概念的推广(1)定义:角可以看成平面内一条射线绕着它的端点从一个位置旋转到另一个位置所成的图形.(2)分类(3)终边相同的角:所有与角α终边相同的角,连同角α在内,可构成一个集合S={β|β=α+k·360°,k∈Z}.2.弧度制的定义和公式(1)定义:把长度等于半径长的弧所对的圆心角叫做1弧度的角,弧度记作rad.(2)公式:角α的弧度数公式|α|=(l表示弧长)角度与弧度的换算①1°=rad;②1rad=°弧长公式l=|α|r扇形面积公式S=lr=|α|r23.任意角的三角函数三角函数正弦余弦正切定义设α是一个任意角,它的终边与单位圆交于点P(x,y),那么y叫做α的正弦,记作sinαx叫做α的余弦,记作cosα叫做α的正切,记作tanα一+++各象限符号二+--三--+四-+-三角函数线有向线段MP为正弦线有向线段OM为余弦线有向线段AT为正切线[小题体验]1.(2019·海门一中月考)若角α满足α=45°+k·180°,k∈Z,则角α的终边落在第________象限.答案:一、三2.(2018·南京调研)已知角α的终边过点P(-5,12),则cosα=________.答案:-3.已知半径为120mm的圆上,有一条弧的长是144mm,则该弧所对的圆心角的弧度数为________.答案:1.21.注意易混概念的区别:象限角、锐角、小于90°的角是概念不同的三类角.第一类是象限角,第二、第三类是区间角.2.角度制与弧度制可利用180°=πrad进行互化,在同一个式子中,采用的度量制度必须一致,不可混用.3.已知三角函数值的符号确定角的终边位置不要遗漏终边在坐标轴上的情况.4.三角函数的定义中,当P(x,y)是单位圆上的点时有sinα=y,cosα=x,tanα=,但若不是单位圆时,如圆的半径为r,则sinα=,cosα=,tanα=.[小题纠偏]1.(2019·如皋模拟)-为第________象限角.答案:二2.若角α终边上有一点P(x,5),且cosα=(x≠0),则sinα=________.答案:[题组练透]1.(2019·海安模拟)若α是第二象限角,则是第______象限角.解析: α是第二象限角,∴+2kπ<α<π+2kπ,k∈Z,∴+kπ<<+kπ,k∈Z.当k为偶数时,是第一象限角;当k为奇数时,是第三象限角.故是第一或三象限角.答案:一或三2.在-720°~0°范围内所有与45°终边相同的角为________.解析:所有与45°有相同终边的角可表示为:β=45°+k×360°(k∈Z),则令-720°≤45°+k×360°<0°,得-765°≤k×360°<-45°,解得-≤k<-,从而k=-2或k=-1,代入得β=-675°或β=-315°.答案:-675°或-315°3.终边在直线y=x上,且在[-2π,2π)内的角α的集合为________________.解析:如图,在平面直角坐标系中画出直线y=x,可以发现它与x轴的夹角是,在[0,2π)内,终边在直线y=x上的角有两个:,;在[-2π,0)内满足条件的角有两个:-,-,故满足条件的角α构成的集合为.答案:4.设角α是第三象限角,且=-sin,则角是第________象限角.解析:由角α是第三象限角,知2kπ+π<α<2kπ+(k∈Z),则kπ+<<kπ+(k∈Z),故是第二或第四象限角.由=-sin,知sin<0,所以只能是第四象限角.答案:四[谨记通法]1.终边在某直线上角的求法4步骤(1)数形结合,在平面直角坐标系中画出该直线;(2)按逆时针方向写出[0,2π)内的角;(3)再由终边相同角的表示方法写出满足条件角的集合;(4)求并集化简集合.2.确定kα,(k∈N*)的终边位置3步骤(1)用终边相同角的形式表示出角α的范围;(2)再写出kα或的范围;(3)然后根据k的可能取值讨论确定kα或的终边所在位置.[题组练透]1.(2019·盐城模拟)在半径为1的圆中,3弧度的圆心角所对的弧长为________.解析:在半径为1的圆中,3弧度的圆心角所对的弧长l=|α|r=3×1=3.答案:32.已知扇形的周长是6,面积是2,则扇形的圆心角的弧度数是________.解析:设此扇形的半径为r,弧长为l,则解得或从而α===4或α===1.答案:1或43.如果一个扇形的半径变为原来的一半,而弧长变为原来的倍,则该弧所对的圆心角是原来的________倍.解析:设圆的半径为r,弧长为l,则其弧度数为.将半径变为原来的一半,弧长变为原来的倍,则...