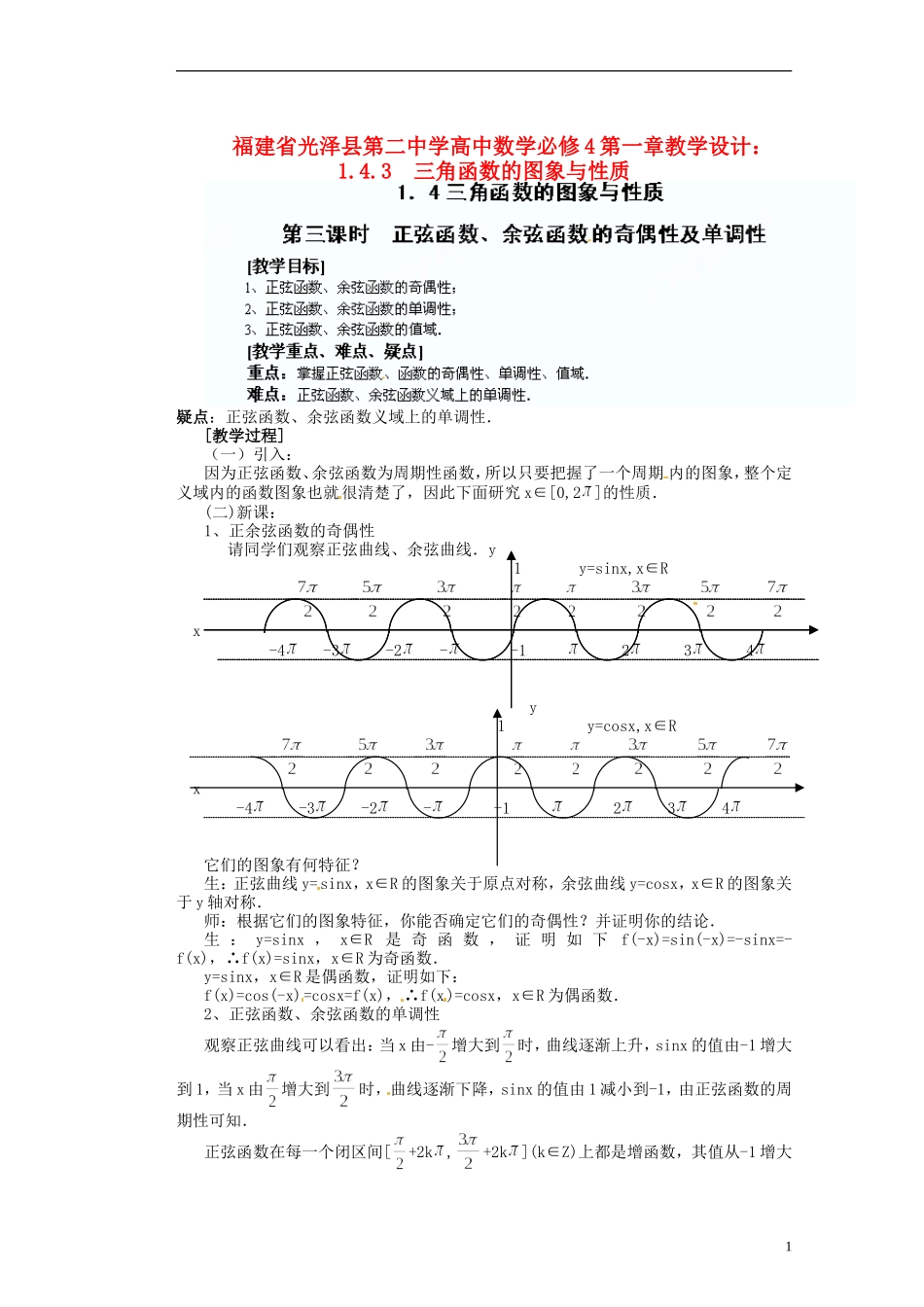
福建省光泽县第二中学高中数学必修4第一章教学设计:1.4.3三角函数的图象与性质疑点:正弦函数、余弦函数义域上的单调性.[教学过程](一)引入:因为正弦函数、余弦函数为周期性函数,所以只要把握了一个周期内的图象,整个定义域内的函数图象也就很清楚了,因此下面研究x∈[0,2]的性质.(二)新课:1、正余弦函数的奇偶性请同学们观察正弦曲线、余弦曲线.y1y=sinx,x∈R----x-4-3-2--1234y1y=cosx,x∈R----x-4-3-2--1234它们的图象有何特征?生:正弦曲线y=sinx,x∈R的图象关于原点对称,余弦曲线y=cosx,x∈R的图象关于y轴对称.师:根据它们的图象特征,你能否确定它们的奇偶性?并证明你的结论.生:y=sinx,x∈R是奇函数,证明如下f(-x)=sin(-x)=-sinx=-f(x),∴f(x)=sinx,x∈R为奇函数.y=sinx,x∈R是偶函数,证明如下:f(x)=cos(-x)=cosx=f(x),∴f(x)=cosx,x∈R为偶函数.2、正弦函数、余弦函数的单调性观察正弦曲线可以看出:当x由-增大到时,曲线逐渐上升,sinx的值由-1增大到1,当x由增大到时,曲线逐渐下降,sinx的值由1减小到-1,由正弦函数的周期性可知.正弦函数在每一个闭区间[+2k,+2k](k∈Z)上都是增函数,其值从-1增大1到1;在每一个闭区间[-+2k,+2k](k∈Z)上都是减函数,其值从1减小到-1.类似地,我们可得到余弦函数的单调性:余弦在每一个闭区间[(2k-1),2k](k∈Z)上都是增函数,其值从-1增大到1;在每一个闭区间[2k,(2k+1)](k∈Z)上都是减函数,其值从1减小到-1.3、正弦函数、余弦函数的最大值、最小值.例题:课本例3,例4,例5[课堂练习]P451,2,3,4,6[小结]本节课学习了正弦函数、余弦函数的值域、奇偶性、单调性,并会利用它们来确定一些函数的值域、比较函数值大小,求函数的单调区间.[课后作业]P522,4,5B:1同步练习:1。判断下列函数的奇偶性(1)(2)f(x)=sin4x-cos4x+cos2x;(3)(4)(5);(6)2。(1)函数f(x)=sinx图象的对称轴是;对称中心是.(2)函数图象的对称轴是;对称中心是.3。已知f(x)=ax+bsin3x+1(a、b为常数),且f(5)=7,求f(-5).4。已知(1)求f(x)的定义域和值域;(2)判断它的奇偶性、周期性;(3)判断f(x)的单调性.5。(1)θ是三角形的一个内角,且关于x的函数f(x)=sain(x+θ)+cos(x-θ)是偶函数,求θ的值.(2)若函数f(x)=sin2x+bcos2x的图象关于直线对称,求b的值.6.已知,试确定函数的奇偶性、单调性.7.不通过求值,指出下列各式大于0还是小于0;①;②(3)比较大小;(4)8.(1)化简:2(2)已知非零常数满足,求的值;(3)已知求值:(1);(2)解:(1)(2)(3)两式平方相加得;两式平方相加得即3