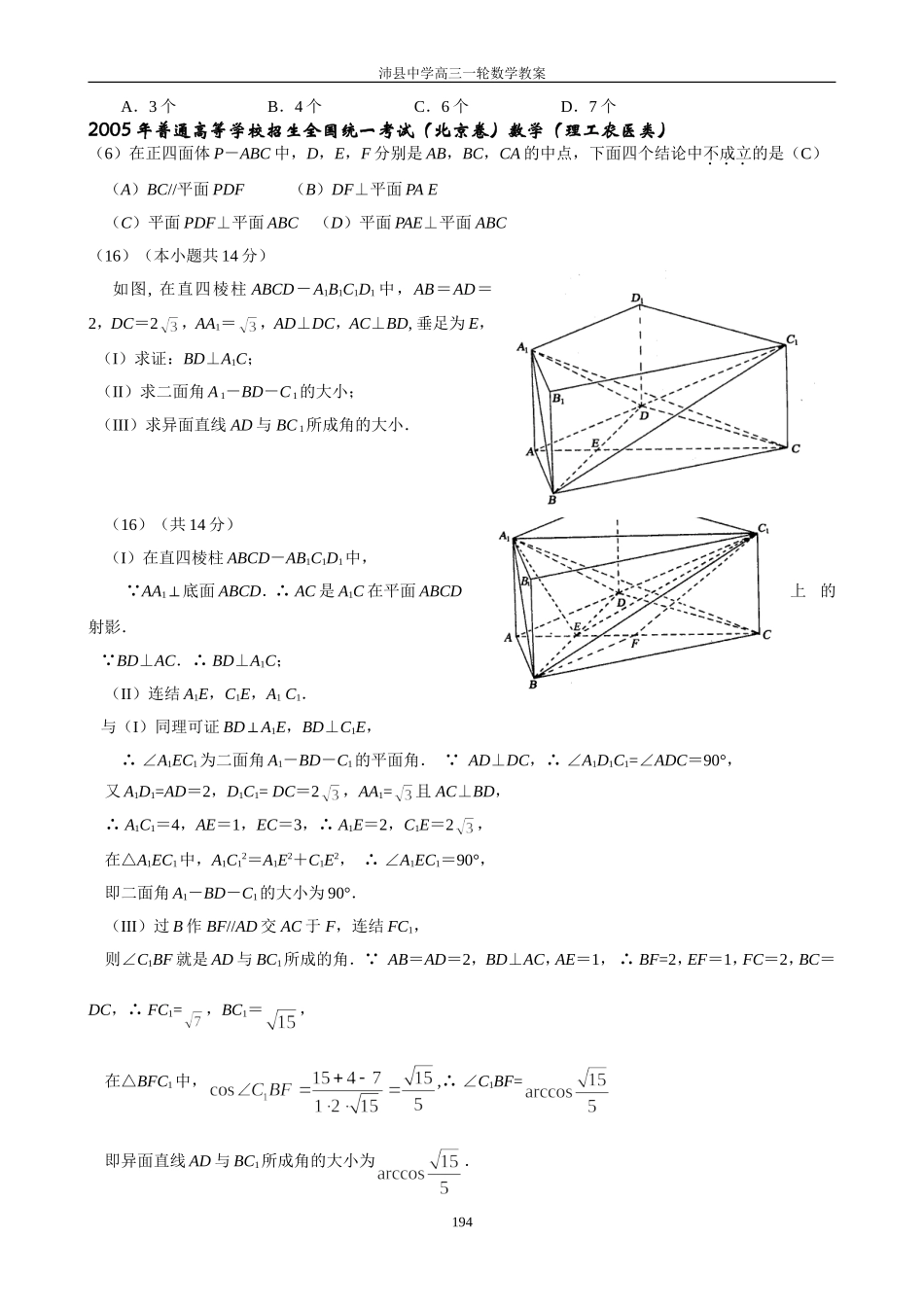
沛县中学高三一轮数学教案1073立体几何综合问题22005全国高考立体几何题河北、河南、山西、安徽(全国卷I)(2)一个与球心距离为1的平面截球所得的圆面面积为,则球的表面积为(C)(A)(B)(C)(D)(4)如图,在多面体ABCDEF中,已知ABCD是边长为1的正方形,且均为正三角形,EF∥AB,EF=2,则该多面体的体积为(C)(A)(B)(C)(D)(16)在正方形中,过对角线的一个平面交于E,交于F,则①四边形一定是平行四边形①四边形有可能是正方形②四边形在底面ABCD内的投影一定是正方形③四边形有可能垂直于平面以上结论正确的为①③④。(写出所有正确结论的编号)2005年普通高等学校招生全国统一考试理科数学(福建卷)4.已知直线m、n与平面、,给出下列三个命题:①若m∥,n∥,则m∥n;②若m∥,n⊥,则n⊥m;③若m⊥,m∥,则⊥.其中真命题的个数是(C)A.0B.1C.2D.38.如图,长方体ABCD-A1B1C1D1中,AA1=AB=2,AD=1,E、F、G分别是DD1、AB、CC1的中点,则异面直线A1E与GF所成的角是(D)A.arccosB.C.arccosD.20.(本小题满分12分)如图,直二面角D-AB-E中,四边形ABCD是边长为2的正方形,AE=EB,F为CE上的点,且BF⊥平面ACE.(Ⅰ)求证:AE⊥平面BCE;(Ⅱ)求二面角B-AC-E的大小;(Ⅲ)求点D到平面ACE的距离。20、(Ⅰ)略;(Ⅱ);(Ⅲ)。2005年普通高等学校招生全国统一考试理科数学(必修+选修Ⅱ)4.设三棱柱ABC—A1B1C1的体积为V,P、Q分别是侧棱AA1、CC1上的点,且PA=QC1,则四棱锥B—APQC的体积为(C)A.B.C.D.11.不共面的四个定点到平面的距离都相等,这样的平面共有(D)193EGFD1DC1B1A1CBAEFDCBA沛县中学高三一轮数学教案A.3个B.4个C.6个D.7个2005年普通高等学校招生全国统一考试(北京卷)数学(理工农医类)(6)在正四面体P-ABC中,D,E,F分别是AB,BC,CA的中点,下面四个结论中不成立的是(C)(A)BC//平面PDF(B)DF⊥平面PAE(C)平面PDF⊥平面ABC(D)平面PAE⊥平面ABC(16)(本小题共14分)如图,在直四棱柱ABCD-A1B1C1D1中,AB=AD=2,DC=2,AA1=,AD⊥DC,AC⊥BD,垂足为E,(I)求证:BD⊥A1C;(II)求二面角A1-BD-C1的大小;(III)求异面直线AD与BC1所成角的大小.(16)(共14分)(I)在直四棱柱ABCD-AB1C1D1中, AA1⊥底面ABCD.∴AC是A1C在平面ABCD上的射影. BD⊥AC.∴BD⊥A1C;(II)连结A1E,C1E,A1C1.与(I)同理可证BD⊥A1E,BD⊥C1E,∴∠A1EC1为二面角A1-BD-C1的平面角. AD⊥DC,∴∠A1D1C1=∠ADC=90°,又A1D1=AD=2,D1C1=DC=2,AA1=且AC⊥BD,∴A1C1=4,AE=1,EC=3,∴A1E=2,C1E=2,在△A1EC1中,A1C12=A1E2+C1E2,∴∠A1EC1=90°,即二面角A1-BD-C1的大小为90°.(III)过B作BF//AD交AC于F,连结FC1,则∠C1BF就是AD与BC1所成的角. AB=AD=2,BD⊥AC,AE=1,∴BF=2,EF=1,FC=2,BC=DC,∴FC1=,BC1=,在△BFC1中,,∴∠C1BF=即异面直线AD与BC1所成角的大小为.194沛县中学高三一轮数学教案2005年高考全国卷Ⅲ数学(四川、陕西、云南等地区用)(19)(本小题满分12分)在四棱锥V-ABCD中,底面ABCD是正方形,侧面VAD是正三角形,平面VAD⊥底面ABCD.(Ⅰ)证明AB⊥平面VAD.(Ⅱ)求面VAD与面VDB所成的二面角的大小.(19)证明:(Ⅰ)作AD的中点O,则VO⊥底面ABCD.…………………………1分建立如图空间直角坐标系,并设正方形边长为1,…………………………2分则A(,0,0),B(,1,0),C(-,1,0),D(-,0,0),V(0,0,),,,又AB∩AV=A∴AB⊥平面VAD(Ⅱ)由(Ⅰ)得是面VAD的法向量,设是面VDB的法向量,则∴,又由题意知,面VAD与面VDB所成的二面角,所以其大小为2005年广东省高考数学试题(7)给出下列关于互不相同的直线和平面的四个命题:①则与m不共面;②、m是异面直线,;③若;195DCBAVZYXODCBAV沛县中学高三一轮数学教案④若,则其中为假命题的是(C)(A)①(B)②(C)③(D)④16.如图,PA=BC=6,AB=8,PB=AC=10,,F是线段PB上一点,,点E在线段AB上,且EF⊥PB(I)求证:PB⊥平面CEF(II)求二面角B—CE—F的大小...