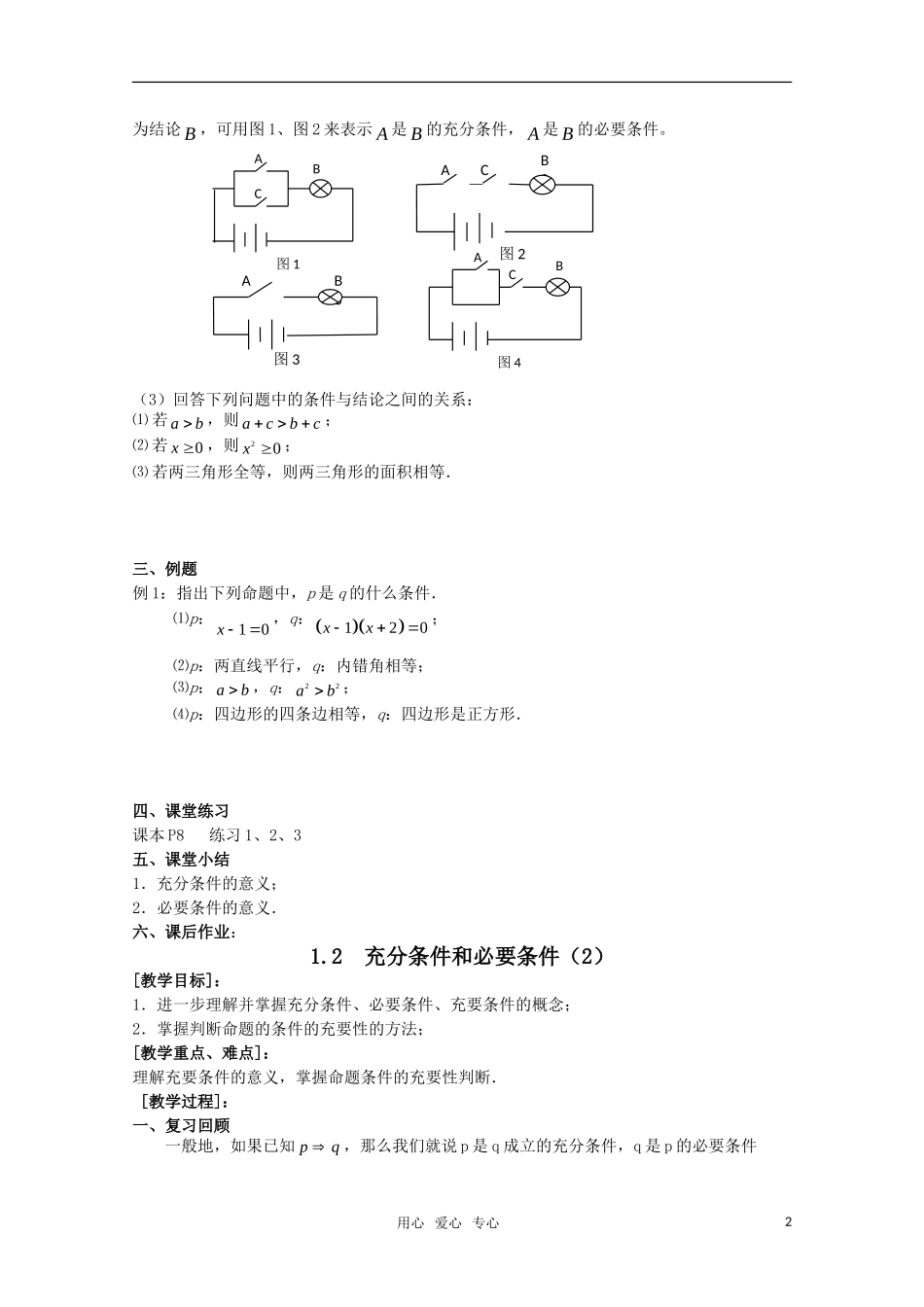
1.2充分条件和必要条件(1)【教学目标】1.从不同角度帮助学生理解充分条件、必要条件与充要条件的意义;2.结合具体命题,初步认识命题条件的充分性、必要性的判断方法;3.培养学生的抽象概括和逻辑推理的意识.【教学重点】构建充分条件、必要条件的数学意义;【教学难点】命题条件的充分性、必要性的判断.【教学过程】一、复习回顾1.命题:可以判断真假的语句,可写成:若p则q.2.四种命题及相互关系:3.请判断下列命题的真假:(1)若xy,则22xy;(2)若22xy,则xy;(3)若1x,则21x;(4)若21x,则1x二、讲授新课1.推断符号“”的含义:一般地,如果“若p,则q”为真,即如果p成立,那么q一定成立,记作:“pq”;如果“若p,则q”为假,即如果p成立,那么q不一定成立,记作:“pq”.用推断符号“和”写出下列命题:⑴若ab,则acbc;⑵若ab,则acbc;2.充分条件与必要条件一般地,如果pq,那么称p是q的充分条件;同时称q是p的必要条件.如何理解充分条件与必要条件中的“充分”和“必要”呢?由上述定义知“pq”表示有p必有q,所以p是q的充分条件,这点容易理解.但同时说q是p的必要条件是为什么呢?q是p的必要条件说明没有q就没有p,q是p成立的必不可少的条件,但有q未必一定有p.充分性:说条件是充分的,也就是说条件是充足的,条件是足够的,条件是足以保证的.它符合上述的“若p则q”为真(即pq)的形式.“有之必成立,无之未必不成立”.必要性:必要就是必须,必不可少.它满足上述的“若非q则非p”为真(即qp)的形式.“有之未必成立,无之必不成立”.命题按条件和结论的充分性、必要性可分为四类:(1)充分必要条件(充要条件),即pq且qp;(2)充分不必要条件,即pq且qp;(3)必要不充分条件,即pq且qp;(4)既不充分又不必要条件,即pq且qp.3.从不同角度理解充分条件、必要条件的意义(1)借助“子集概念”理解充分条件与必要条件。设,AB为两个集合,集合AB是指xAxB。这就是说,“xA”是“xB”的充分条件,“xB”是“xA”的必要条件。对于真命题“若p则q”,即pq,若把p看做集合A,把q看做集合B,“pq”相当于“AB”。(2)借助“电路图”理解充分条件与必要条件。设“开关A闭合”为条件A,“灯泡B亮”用心爱心专心1B3AC图2CAB图4CAB图1图3B3A为结论B,可用图1、图2来表示A是B的充分条件,A是B的必要条件。(3)回答下列问题中的条件与结论之间的关系:⑴若ab,则acbc;⑵若0x,则20x;⑶若两三角形全等,则两三角形的面积相等.三、例题例1:指出下列命题中,p是q的什么条件.⑴p:10x,q:120xx;⑵p:两直线平行,q:内错角相等;⑶p:ab,q:22ab;⑷p:四边形的四条边相等,q:四边形是正方形.四、课堂练习课本P8练习1、2、3五、课堂小结1.充分条件的意义;2.必要条件的意义.六、课后作业:1.2充分条件和必要条件(2)[教学目标]:1.进一步理解并掌握充分条件、必要条件、充要条件的概念;2.掌握判断命题的条件的充要性的方法;[教学重点、难点]:理解充要条件的意义,掌握命题条件的充要性判断.[教学过程]:一、复习回顾一般地,如果已知pq,那么我们就说p是q成立的充分条件,q是p的必要条件用心爱心专心2⑴“abc”是“0abbcca”的充分不必要条件.⑵若a、b都是实数,从①0ab;②0ab;③0ab;④0ab;⑤220ab;⑥220ab中选出使a、b都不为0的充分条件是①②⑤.二、例题分析条件充要性的判定结果有四种,判定的方法很多,但针对各种具体情况,应采取不同的策略,灵活判断.下面我们来看几个充要性的判断及其证明的例题.1.要注意转换命题判定,培养思维的灵活性例1:已知p:2xy;q:x、y不都是1,p是q的什么条件?分析:要考虑p是q的什么条件,就是判断“若p则q”及“若q则p”的真假性从正面很难判断是,我们从它们的逆否命题来判断其真假性“若p则q”的逆否命题是“若x、y都是1,则2xy”真的“若q则p”的逆否命题是“若2xy,则x、y都...