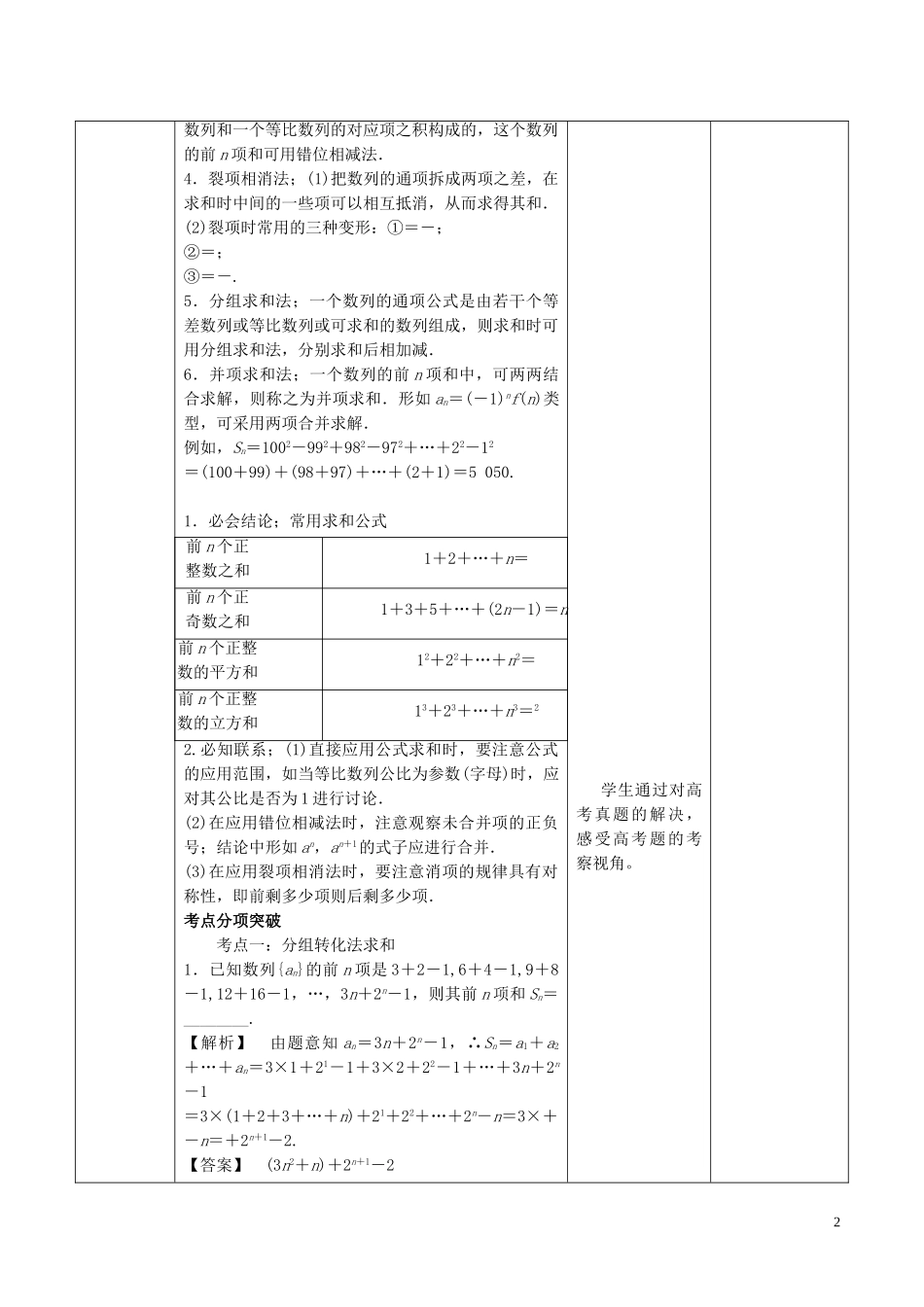
数列求和【教学目标】1.熟练掌握等差、等比数列的前n项和公式.2.掌握非等差、等比数列求和的几种常见方法.3.能在具体的问题情境中识别数列的等差关系或等比关系,并能用相关知识解决相应的问题.【重点难点】1.教学重点:识别数列的等差关系或等比关系,并能用相关知识解决相应的问题;2.教学难点:学会对知识进行整理达到系统化,提高分析问题和解决问题的能力;【教学策略与方法】自主学习、小组讨论法、师生互动法【教学过程】教学流程教师活动学生活动设计意图考纲传真:1.熟练掌握等差、等比数列的前n项和公式.2.掌握非等差、等比数列求和的几种常见方法.3.能在具体的问题情境中识别数列的等差关系或等比关系,并能用相关知识解决相应的问题.真题再现;1.(2015·全国Ⅱ,16)设Sn是数列{an}的前n项和,且a1=-1,an+1=SnSn+1,则Sn=____________.解析由题意,得S1=a1=-1,又由an+1=SnSn+1,得Sn+1-Sn=SnSn+1,因为Sn≠0,所以=1,即-=-1,故数列是以=-1为首项,-1为公差的等差数列,得=-1-(n-1)=-n,所以Sn=-.答案-2.(2013·全国Ⅱ,3)等比数列{an}的前n项和为Sn.已知S3=a2+10a1,a5=9,则a1=()A.B.-C.D.-解析设公比为q,则由S3=a2+10a1,得a1+a2+a3-a2=10a1,故a3=9a1,所以q2=9.由a5=9,得a1=.答案C知识梳理:知识点数列求和的常见方法1.公式法;直接利用等差数列、等比数列的前n项和公式求和(1)等差数列的前n项和公式:Sn==na1+d.(2)等比数列的前n项和公式:Sn=2.倒序相加法;如果一个数列{an}的前n项中首末两端等“距离”的两项的和相等或等于同一个常数,那么求这个数列的前n项和即可用倒序相加法,如等差数列的前n项和公式即是用此法推导的.3.错位相减法;如果一个数列的各项是由一个等差。学生通过对高考真题的解决,发现自己对知识的掌握情况。通过对考纲的解读和分析。让学生明确考试要求,做到有的放矢1数列和一个等比数列的对应项之积构成的,这个数列的前n项和可用错位相减法.4.裂项相消法;(1)把数列的通项拆成两项之差,在求和时中间的一些项可以相互抵消,从而求得其和.(2)裂项时常用的三种变形:①=-;②=;③=-.5.分组求和法;一个数列的通项公式是由若干个等差数列或等比数列或可求和的数列组成,则求和时可用分组求和法,分别求和后相加减.6.并项求和法;一个数列的前n项和中,可两两结合求解,则称之为并项求和.形如an=(-1)nf(n)类型,可采用两项合并求解.例如,Sn=1002-992+982-972+…+22-12=(100+99)+(98+97)+…+(2+1)=5050.1.必会结论;常用求和公式前n个正整数之和1+2+…+n=前n个正奇数之和1+3+5+…+(2n-1)=n前n个正整数的平方和12+22+…+n2=前n个正整数的立方和13+23+…+n3=22.必知联系;(1)直接应用公式求和时,要注意公式的应用范围,如当等比数列公比为参数(字母)时,应对其公比是否为1进行讨论.(2)在应用错位相减法时,注意观察未合并项的正负号;结论中形如an,an+1的式子应进行合并.(3)在应用裂项相消法时,要注意消项的规律具有对称性,即前剩多少项则后剩多少项.考点分项突破考点一:分组转化法求和1.已知数列{an}的前n项是3+2-1,6+4-1,9+8-1,12+16-1,…,3n+2n-1,则其前n项和Sn=________.【解析】由题意知an=3n+2n-1,∴Sn=a1+a2+…+an=3×1+21-1+3×2+22-1+…+3n+2n-1=3×(1+2+3+…+n)+21+22+…+2n-n=3×+-n=+2n+1-2.【答案】(3n2+n)+2n+1-2学生通过对高考真题的解决,感受高考题的考察视角。2环节二:2.(2015·福建高考)等差数列{an}中,a2=4,a4+a7=15.(1)求数列{an}的通项公式;(2)设bn=2an-2+n,求b1+b2+b3+…+b10的值.【解】(1)设等差数列{an}的公差为d,由已知得解得所以an=a1+(n-1)d=n+2.(2)由(1)可得bn=2n+n,所以b1+b2+b3+…+b10=(2+1)+(22+2)+(23+3)+…+(210+10)=(2+22+23+…+210)+(1+2+3+…+10)=+=(211-2)+55=211+53=2101.归纳:分组转化法求和的常见类型1.若an=bn±cn,且{bn},{cn}为等差或等比数...