高中数学 任意角的三角函数（二）教案 新人教A版必修4VIP免费

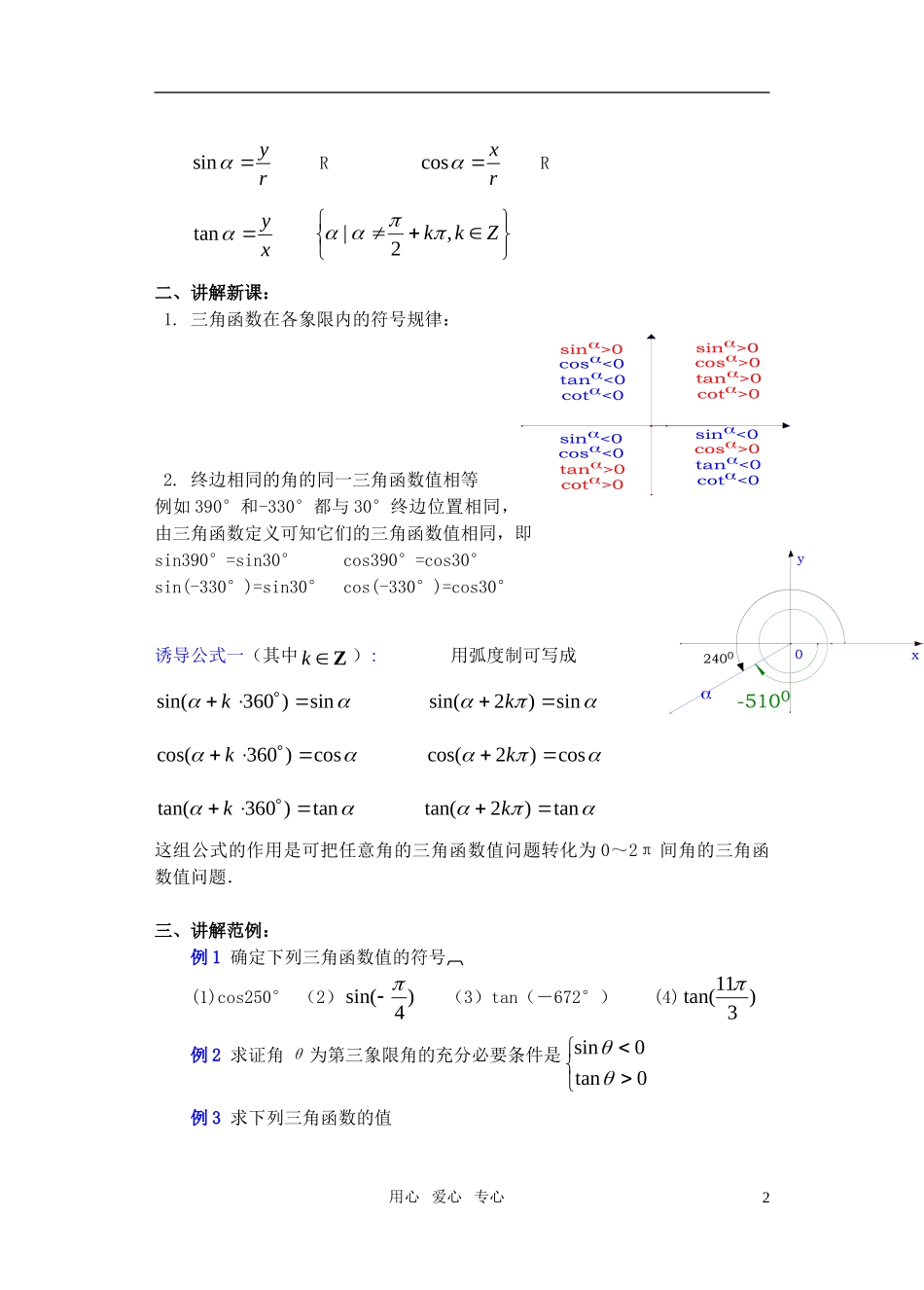
4.3任意角的三角函数（二）教学目的：1.理解并掌握各种三角函数在各象限内的符号.2.理解并掌握终边相同的角的同一三角函数值相等.教学重点：三角函数在各象限内的符号,终边相同的角的同一三角函数值相等奎屯王新敞新疆教学难点：正确理解三角函数可看作以“实数”为自变量的函数奎屯王新敞新疆授课类型：新授课奎屯王新敞新疆教学过程：一、复习引入：1.设是一个任意角，在的终边上任取（异于原点的）一点P（x,y）则P与原点的距离02222yxyxr2.比值ry叫做的正弦记作：rysin比值rx叫做的余弦记作：rxcos比值xy叫做的正切记作：xytan比值yx叫做的余切记作：yxcot以上四种函数，统称为三角函数.3.突出探究的几个问题：①角是“任意角”，当=2k+(kZ)时，与的同名三角函数值应该是相等的，即凡是终边相同的角的三角函数值相等奎屯王新敞新疆②实际上，如果终边在坐标轴上，上述定义同样适用奎屯王新敞新疆③三角函数是以“比值”为函数值的函数④0r而x,y的正负是随象限的变化而不同，故三角函数的符号应由象限确定.⑤定义域：用心爱心专心1ry)(x,PrysinRrxcosRxytanZkk,2|二、讲解新课：1.三角函数在各象限内的符号规律：2.终边相同的角的同一三角函数值相等例如390°和-330°都与30°终边位置相同，由三角函数定义可知它们的三角函数值相同，即sin390°=sin30°cos390°=cos30°sin(-330°)=sin30°cos(-330°)=cos30°诱导公式一（其中Zk）:用弧度制可写成sin)360sin(ksin)2sin(kcos)360cos(kcos)2cos(ktan)360tan(ktan)2tan(k这组公式的作用是可把任意角的三角函数值问题转化为0～2π间角的三角函数值问题．三、讲解范例：例1确定下列三角函数值的符号(1)cos250°（2）)4sin(（3）tan（－672°）(4))311tan(例2求证角θ为第三象限角的充分必要条件是0tan0sin例3求下列三角函数的值用心爱心专心20xy2400-5100cot<0tan<0cos>0sin<0cot>0tan>0cos<0sin<0cot<0tan<0cos<0sin>0sin>0tan>0cot>0cos>0(1)sin1480°10′(2)49cos（3）)611tan(.例4求值：sin(-1320°)cos1110°+cos(-1020°)sin750°+tg4950°．四、课堂练习：1.确定下列各式的符号(1)sin100°·cos240°(2)sin5+tan52..x取什么值时,xxxtancossin有意义?3．若三角形的两内角，满足sincos0，则此三角形必为……（B）A锐角三角形B钝角三角形C直角三角形D以上三种情况都可能4．若是第三象限角，则下列各式中不成立的是………………（B）A：sin+cos0B：tansin0C：coscot0D：cotcsc05．已知是第三象限角且02cos，问2是第几象限角？6．已知1212sin，则为第几象限角？五、小结本节课我们重点讨论了两个内容，一是三角函数在各象限内的符号，二是一组公式，两者的作用分别是：前者确定函数值的符号，后者将任意角的三角函数化为0°到360°角的三角函数，这两个内容是我们日后学习的基础.六、课后作业：1.确定下列三角函数值符号：(1)tan(125560)(2)cos5162.化简222222sin1cos1cossincottana.用心爱心专心3