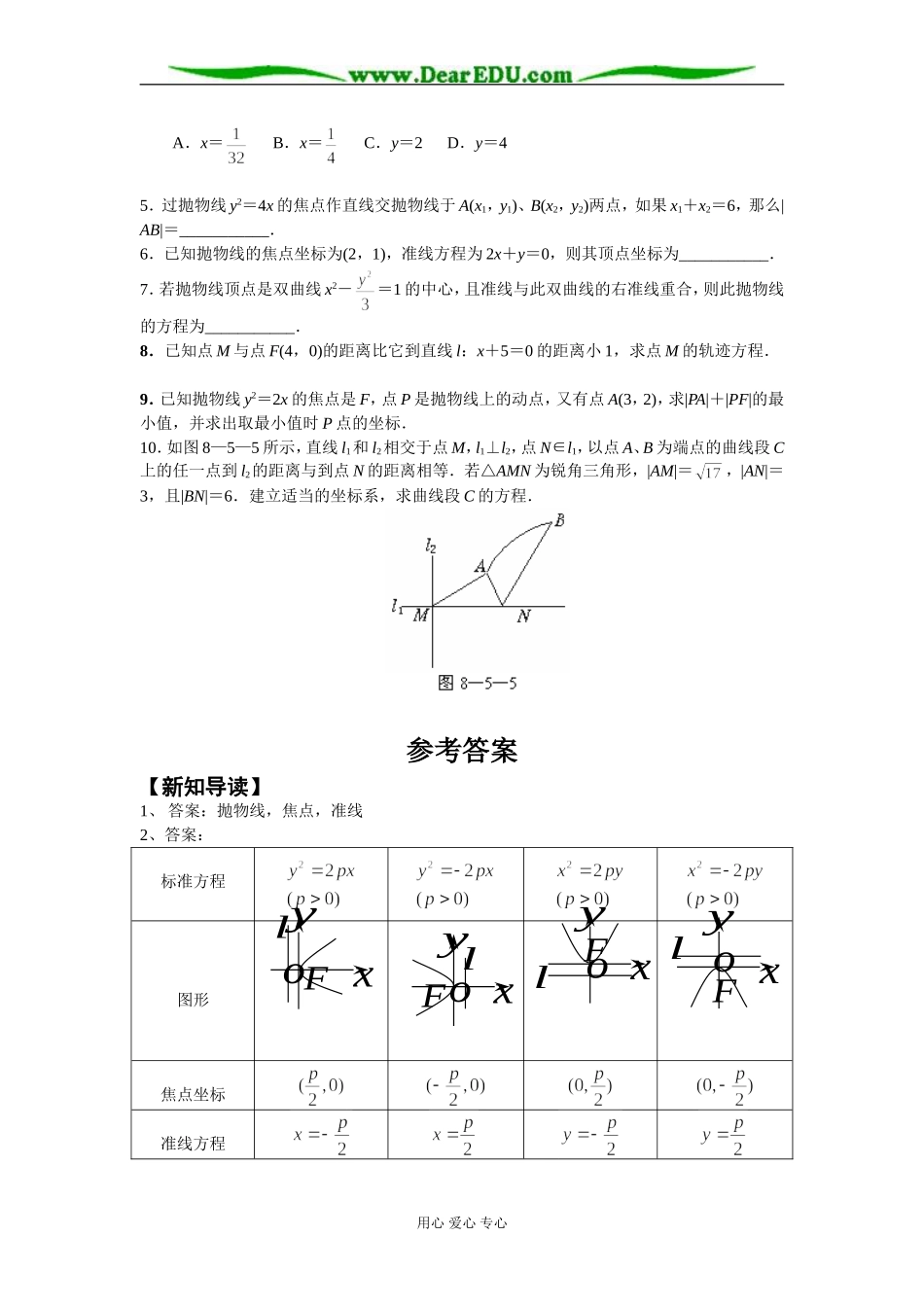
抛物线的标准方程【新知导读】1.平面内与一定点F和一条定直线l的距离相等的点的轨迹叫做(定点F不在定直线l上).定点F叫做抛物线的,定直线l叫做抛物线的.2.填写下表:标准方程图形焦点坐标准线方程3.抛物线的准线方程是()A.B.C.D.【范例点睛】【例1】斜率为1的直线经过抛物线y2=4x的焦点,与抛物线交于两点A、B,求线段AB的长.策略:本题是直线与抛物线的位置关系问题.处理方法同前面椭圆、双曲线内容.其基本思路:一、建立直线方程与抛物线方程的联立方程组,解出A、B两点的坐标,用距离公式;二、利用韦达定理及弦长公式求解;三、利用抛物线的定义,|AB|=xA+xB+p求解.解:如图所示,由抛物线的标准方程可知,焦点F(1,0),准线方程为x=-1,由题设,直线AB的方程为y=x-1,代入抛物线方程y2=4x,整理得x2-6x+1=0.解法一:解上述方程得:x1=3+2,x2=3-2,分别代入直线方程得y1=2+2,y2=2-2,即A、B的坐标分别为(3+2,2+2)、(3-2,2-2)用心爱心专心oxylyoFloxyFloxyFl∴|AB|==8解法二:设A(x1,y1)、B(x2,y2),则x1+x2=6,x1x2=1∴|AB|=|x1-x2|===8.解法三:设A(x1,y1)、B(x2,y2),由抛物线定义可知,|AF|=|AA′|=x1+1,|BF|=x2+1∴|AB|=x1+x2+2=6+2=8.评注:本题是一个有关抛物线的焦点弦问题,其解题思想值得研究.【例2】求适合下列条件的抛物线的标准方程:(1)过点(-3,2);(2)焦点在直线x-2y-4=0上.策略:根据已知条件求出抛物线的标准方程中的p即可,注意标准方程的形式.解:(1)设抛物线方程为y2=-2px或x2=2py(y>0),将点(-3,2)代入方程得2p=或2p=,∴所求抛物线方程为y2=-x或x2=y.(2)令x=0,由方程x-2y-4=0得y=-2.∴抛物线的焦点为F(0,-2).设抛物线方程为x2=-2py,则由=2,得2p=8,∴所求的抛物线方程为x2=-8y.或令y=0,由x-2y-4=0得x=4,∴抛物线焦点为F(4,0).设抛物线方程为y2=2px,由=4得p=8.则所求方程为y2=16x.总之,所求抛物线方程为x2=-8y或y2=16x.评注:此两小题都有两解,注意不要丢解.做题前可先画草图,全面考查已知条件.本题都采用了待定系数法求解,要注意解题方法和技巧.所求抛物线方程为y2=-x或x2=y.所求抛物线方程为x2=-8y或y2=16x.【自我检测】1.动点P到直线x+4=0的距离减去它到M(2,0)的距离之差是2,则点P的轨迹是()A.直线B.椭圆C.双曲线D.抛物线2.抛物线的顶点在原点,对称轴是x轴,抛物线上一点(-5,2)到焦点距离是6,则抛物线的方程是()A.y2=-2xB.y2=-4xC.y2=2xD.y2=-4x或y2=-36x3.抛物线的顶点在坐标原点,焦点是椭圆4x2+y2=1的一个焦点,则此抛物线的焦点到准线的距离为()A.2B.C.D.4.抛物线y=-x2的准线方程是()用心爱心专心A.x=B.x=C.y=2D.y=45.过抛物线y2=4x的焦点作直线交抛物线于A(x1,y1)、B(x2,y2)两点,如果x1+x2=6,那么|AB|=___________.6.已知抛物线的焦点坐标为(2,1),准线方程为2x+y=0,则其顶点坐标为___________.7.若抛物线顶点是双曲线x2-=1的中心,且准线与此双曲线的右准线重合,则此抛物线的方程为___________.8.已知点M与点F(4,0)的距离比它到直线l:x+5=0的距离小1,求点M的轨迹方程.9.已知抛物线y2=2x的焦点是F,点P是抛物线上的动点,又有点A(3,2),求|PA|+|PF|的最小值,并求出取最小值时P点的坐标.10.如图8—5—5所示,直线l1和l2相交于点M,l1⊥l2,点N∈l1,以点A、B为端点的曲线段C上的任一点到l2的距离与到点N的距离相等.若△AMN为锐角三角形,|AM|=,|AN|=3,且|BN|=6.建立适当的坐标系,求曲线段C的方程.参考答案【新知导读】1、答案:抛物线,焦点,准线2、答案:标准方程图形焦点坐标准线方程用心爱心专心oFxylxyoFloxyFloxyFl2、答:C【自我检测】1.答案:D解析:因为点P到直线x=-4的距离比到定点M(2,0)的距离大2,故点P到直线x=-2的距离等于到定点M(2,0)的距离,所以P点轨迹为抛物线.2.答案:B解析:因为点(-5,2)在第二象限,且以原点为顶点,x轴为对称轴,故抛物线开口向左,设其方...