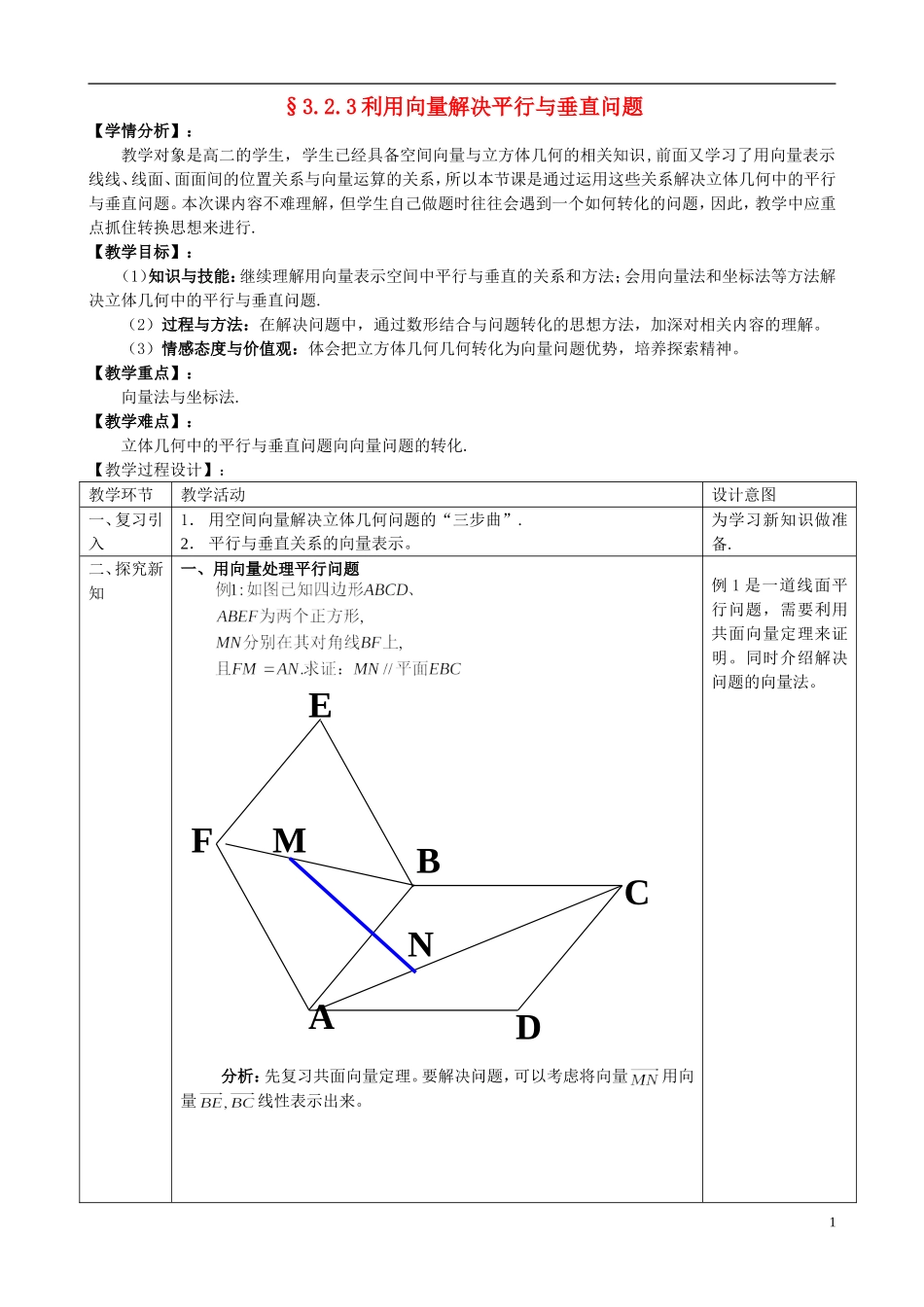
§3.2.3利用向量解决平行与垂直问题【学情分析】:教学对象是高二的学生,学生已经具备空间向量与立方体几何的相关知识,前面又学习了用向量表示线线、线面、面面间的位置关系与向量运算的关系,所以本节课是通过运用这些关系解决立体几何中的平行与垂直问题。本次课内容不难理解,但学生自己做题时往往会遇到一个如何转化的问题,因此,教学中应重点抓住转换思想来进行.【教学目标】:(1)知识与技能:继续理解用向量表示空间中平行与垂直的关系和方法;会用向量法和坐标法等方法解决立体几何中的平行与垂直问题.(2)过程与方法:在解决问题中,通过数形结合与问题转化的思想方法,加深对相关内容的理解。(3)情感态度与价值观:体会把立方体几何几何转化为向量问题优势,培养探索精神。【教学重点】:向量法与坐标法.【教学难点】:立体几何中的平行与垂直问题向向量问题的转化.【教学过程设计】:教学环节教学活动设计意图一、复习引入1.用空间向量解决立体几何问题的“三步曲”.2.平行与垂直关系的向量表示。为学习新知识做准备.二、探究新知一、用向量处理平行问题分析:先复习共面向量定理。要解决问题,可以考虑将向量用向量线性表示出来。例1是一道线面平行问题,需要利用共面向量定理来证明。同时介绍解决问题的向量法。ADCBEFNM1评注:向量p与两个不共线的向量a、b共面的充要条件是存在实数对x,y使p=xa+yb.利用共面向量定理可以证明线面平行问题。本题用的就是向量法。(图略)分析:面面平行线面平行线线平行。评注:由于三种平行关系可以相互转化,所以本题可用逻辑推理来证明。用向量法将逻辑论证转化为问题的算法化,在应用向量法时需要合理建立空间直角坐标系,方能减少运算量。本题选用了坐标法。思考:一般应如何建立空间直角坐标系?二、用向量处理垂直问题联系共线向量来理解。例2是关于面面平行的问题,联系几何定理与向量平行。同时介绍解决问题的坐标法。[来源:Zxxk.Com]例3是线面垂直问题,图形和例2一样是正方体,可进一步训练坐标,,.FBANAC�存在实数使FM()()()(1).MNMFFAANBFEBACBEBAABADEBBEADEBBEBCBEBEBC���:,,,BEABFMANFBAC证明在正方形ABCD与ABEF中,11111:,,DADCDDxyz证明如图分别以、、三边所在的直线为轴建立空间直角坐标系.设正方体的棱长为1,111(1,0,0),(1,1,0),(0,0,1),(0,0,1)(1,0,1),(1,0,1)ABCDDBC�1则则A1111111111111//.////.//.//.ADBCADBCADCBDABCBDABDCBD�即直线,则平面同理右证:平面平面平面2ABCDO三、练习巩固分别用向量法和坐标法解决以下问题:向量法:所以,结论成立。坐标法:证明:(图略)巩固知识,培养技能.四、小结利用向量解决平行与垂直问题反思归纳.2/1,0,0,,',1cbcabaACcABbAAa设证明:设底面边长为bacCCACBABCabBBABABacACAACA''''''2222(2)()(2)()22110caabbaabbaaabbab����������������).,1,0('),,1,0('),,0,3(').0,1,0(),0,1,0(),0,0,3(.,,2hChBhACBAh系如图建立空间直角坐标高为设底面边长为2220''31,2.''020.''ABAChhABBChBCAB��3A'B'CBC'A1.向量法:利用向量的概念技巧运算解决问题。2.坐标法:利用数及其运算解决问题。两种方法经常结合起来使用。五、作业1,直三棱柱中,角ACB是直角,AC=1,CB=,侧棱=1,侧面的两条对角线交点为D,的中点为M,求证CD平面BDM。2,课本p111第1、3题。练习与测试:(基础题)1,直三棱柱ABC—A1B1C1中,若,则()A.+-B.-+C.-++D.-+-答:D2,若向量、()A.B.C.D.以上三种情况都可能答:B3,一空间四边形ABCD的对边AB与CD,AD与BC都互相垂直,用向量证明:AC与BD也互相垂直.证明:.又,即.……①.又,即.……②由①+②得:即..4,如图,已知矩形ABCD所在平面外一点P,PA⊥平面ABCD,E、F分别是AB、PC的中点.(1)求证:EF∥平面PAD;(2)求证:EF⊥CD;证:如图,建立空间直角坐标系A-xyz,设AB=2a,BC...