内蒙古赤峰二中高中数学 3.2高次不等式与分式不等式的解法教案 新人教B版必修5VIP免费

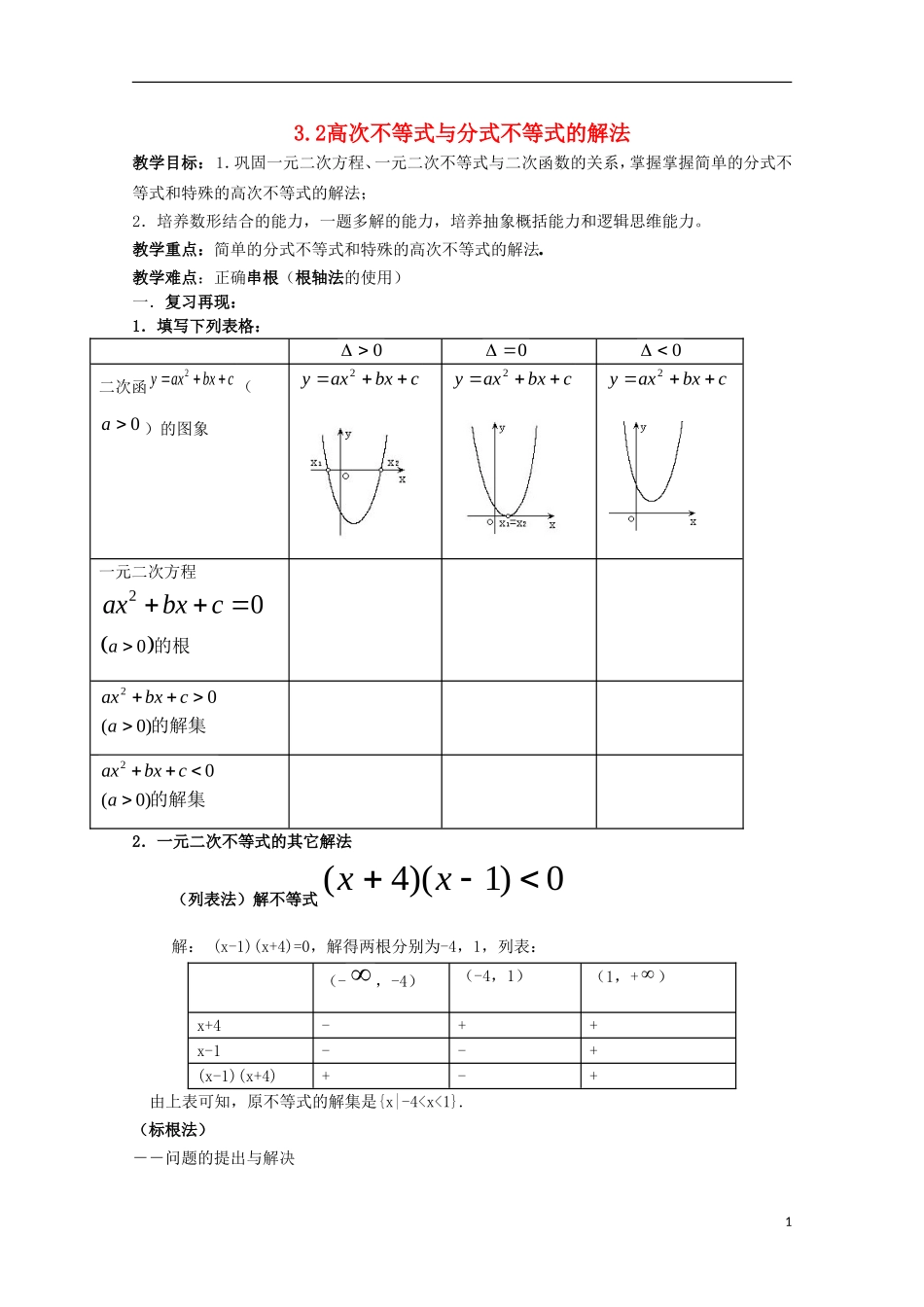
3.2高次不等式与分式不等式的解法教学目标：1．巩固一元二次方程、一元二次不等式与二次函数的关系，掌握掌握简单的分式不等式和特殊的高次不等式的解法；2．培养数形结合的能力，一题多解的能力，培养抽象概括能力和逻辑思维能力。教学重点：简单的分式不等式和特殊的高次不等式的解法奎屯王新敞新疆教学难点：正确串根（根轴法的使用）一．复习再现：1．填写下列表格：000二次函cbxaxy2（0a）的图象cbxaxy2cbxaxy2cbxaxy2一元二次方程20axbxc0a的根的解集)0(02acbxax的解集)0(02acbxax2．一元二次不等式的其它解法（列表法）解不等式0)1)(4(xx解：(x-1)(x+4)=0，解得两根分别为-4，1，列表：（-，-4）（-4，1）（1，+）x+4-++x-1--+(x-1)(x+4)+-+由上表可知，原不等式的解集是{x|-40；例2：解不等式：(x+1)(x+2)(x-3)(x+4)<0；例3:解不等式：(x-2)2(x-3)3(x+1)(x-1)<0.【变式】(x-2)2(x-3)3(x+1)(x-1)0.【归纳】在数轴上表示各根并穿线，每个根穿一次（自右上方开始归纳为"奇过偶不过".例4:解不等式：073xx.例5:解不等式：0322322xxxx.例6:解不等式1116xx【归纳】分式不等式，切忌去分母，一律移项通分化为)()(xgxf>0(或)()(xgxf0)的形式，转化为：()()0()()0()()0fxgxfxgxgx或，即转为一次、二次或特殊高次不等式形式三、小结：四、作业：A.1．解不等式：x(x-3)(2-x)(x+1)>0.2．解不等式：(x-3)(x+1)(x2+4x+4)0.3．求不等式)2()2()23()1()2(22334xxxxxx的解集B.若不等式1122xxbxxxax的解为121x,求ba,的值23.K为何值时，13642222xxkkxx恒成立4．对于任意实数x，代数式(5－4a－2a)2x－2(a－1)x－3的值恒为负值，求a的取值范围奎屯王新敞新疆小结：作业：1如果对于任何实数x，不等式kx2－kx＋1>0都成立，求k的取值范围2设α、β是关于方程2x－2(k－1)x＋k＋1=0的两个实根，求y=2＋2关于k的解析式，并求y的取值范围奎屯王新敞新疆【探究】设二次函数f(x)=ax2+bx+c(a>0)，方程f(x)-x=0的两根x1，x2满足axx1021当1,0xx时，证明：x0时，不等式0axbyc的解的区域在直线0axbyc的上方；不等式0axbyc的解的区域在直线0axbyc的下方。(2)b<0时，不等式0axbyc的解的区域在直线0axbyc的下方；不等式0axbyc的解的区域在直线0axbyc的上方。3．不等式组11122200axbycaxbyc的区域问题。三例题分析1．课本94页例12．课本94页例23．不等式3yxb所表示的区域恰好使点（3，4）不在此区域，而点（4，4）在此区域，求b的取值范围。44．已知点A（a,b）在由不等式组002xyxy确定的平面区域内，求A（a,b）所在区域的面积。5．课本95页例3四．小结五．作业1课本105页1，22．课本106页1，23．画出不等式211yx的区域，并求这个区域的面积.5