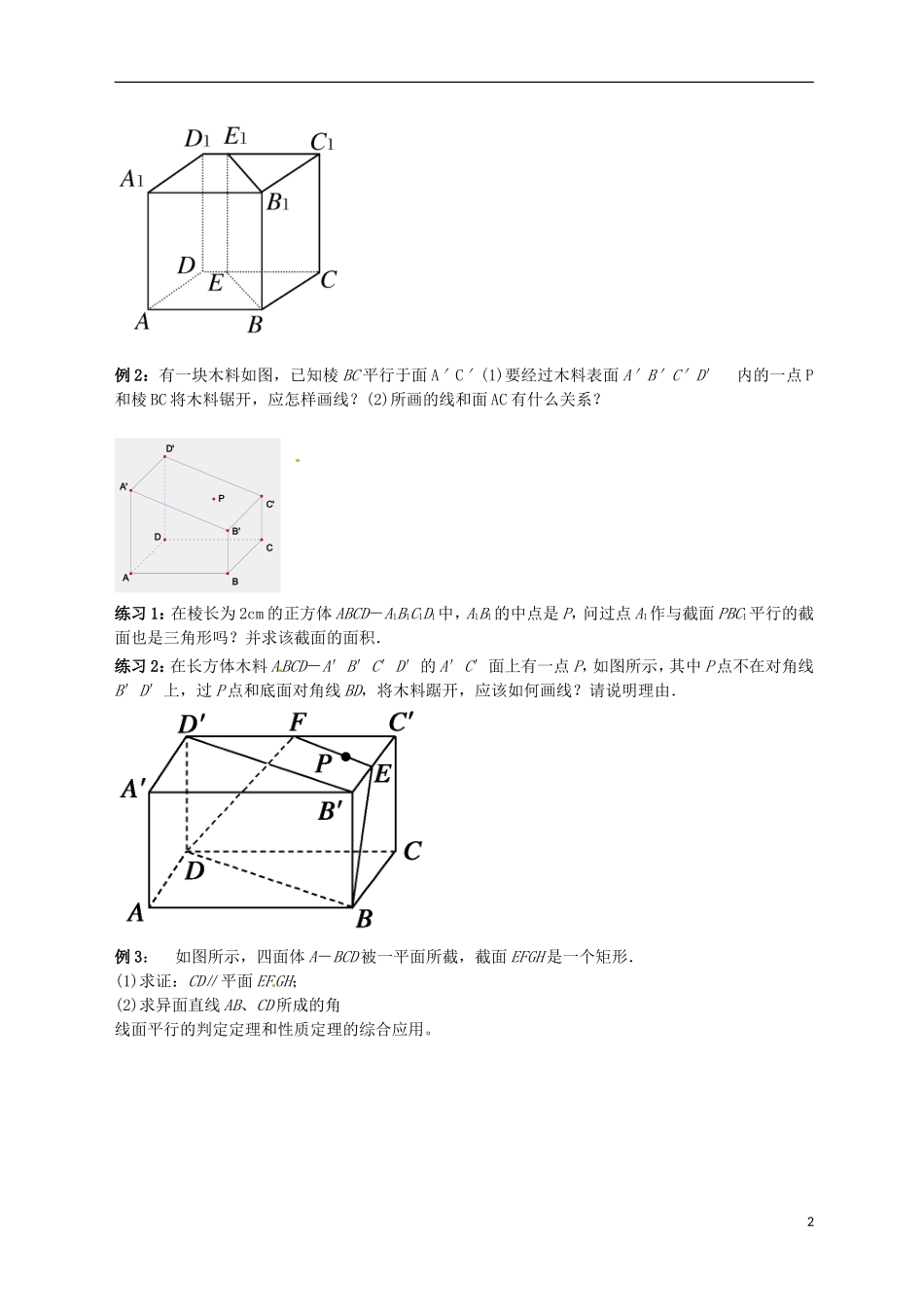
黑龙江省大庆外国语学校高一数学必修二第二章《2.2.3-2.2.4直线与平面、平面与平面平行的性质》学案2学习重、难点学习重点:直线与平面、平面与平面平行的性质及其应用学习难点:将空间问题转化为平面问题的方法,教学过程(一)复习引入:1.空间直线与直线的位置关系2.直线与平面的位置关系3.平面与平面的位置关系4.直线与平面平行的判定定理的符号表示5.平面与平面平行的判定定理的符号表示(二)研探新知A问题1:1)如果一条直线与一个平面平行,那么这条直线与这个平面内的直线有哪些位置关系?(观察长方体)2)教室内日光灯管所在的直线与地面平行,如何在地面上作一条直线与灯管所在的直线平行?)(即如果一条直线和一个平面平行,如何在这个平面内做一条直线与已知直线平行?A问题2:一条直线与平面平行,这条直线和这个平面内直线的位置关系有几种可能?A问题3:如果一条直线与平面α平行,在什么条件下直线与平面α内的直线平行呢?由于直线与平面α内的任何直线无公共点,所以过直线的某一平面,若与平面α相交,则直线就平行于这条交线B自主探究1:已知:∥α,β,α∩β=b。求证:∥b。一、直线与平面平行的性质定理:一条直线与一个平面平行,则过这条直线的任一平面与此平面的交线与该直线平行符号语言:线面平行性质定理作用:证明两直线平行思想:线面平行线线平行解题示例:例1:过正方体AC1的棱BB1作一平面交平面CDD1C1于EE1.求证:BB1∥EE1.线面性质定理应用。1C'D'CDABA'PB'例2:有一块木料如图,已知棱BC平行于面A′C′(1)要经过木料表面A′B′C′D′内的一点P和棱BC将木料锯开,应怎样画线?(2)所画的线和面AC有什么关系?练习1:在棱长为2cm的正方体ABCD-A1B1C1D1中,A1B1的中点是P,问过点A1作与截面PBC1平行的截面也是三角形吗?并求该截面的面积.练习2:在长方体木料ABCD-A′B′C′D′的A′C′面上有一点P,如图所示,其中P点不在对角线B′D′上,过P点和底面对角线BD,将木料踞开,应该如何画线?请说明理由.例3:如图所示,四面体A-BCD被一平面所截,截面EFGH是一个矩形.(1)求证:CD∥平面EFGH;(2)求异面直线AB、CD所成的角线面平行的判定定理和性质定理的综合应用。2例4:已知平面外的两条平行直线中的一条平行于这个平面,求证:另一条也平行于这个平面。小结:作业:习题2。2B组1第二课时:问题:两个平面平行,那么其中一个平面内的直线与另一平面有什么样的关系?两个平面平行,那么其中一个平面内的直线与另一平面内的直线有何关系?例1:如图,平面α,β,γ满足α∥β,α∩γ=a,β∩γ=b,求证:a∥b自主探究平面与平面平行的性质定理平面与平面平行的性质定理:如果两个平行平面同时和第三个平面相交,那么它们的交线平行符号语言:面面平行性质定理作用:思想:例2求证:夹在两个平行平面间的平行线段相等已知:,,,求证:。3问题:若夹在两个平面间的三条平行线段相等,那么这两个平面的位置关系是________.例3.已知:如图,α∥β,点P是平面α,β外的一点,直线PAB、PCD分别与α、β相交于点A、B和C、D:(1)求证:AC∥BD;(2)已知PA=4cm,AB=5cm,PC=3cm,求PD的长.例4如图,已知平面α∥β,直线AB分别交α,β于A、B,直线CD交α、β于C、D,M、N分别在线段AB、CD上,且求证:MN∥平面β.(化异为共)练习:练习册跟踪练习3已知三个平面α、β、γ满足α∥β∥γ,直线a与这三个平面依次交于点4A、B、C,直线b与这三个平面依次交于点E、F、G.求证跟踪练习4:后面作业中4题、10题。61页练习判断命题。2.下列判断正确的是()A.∥α,,则∥bB.∩α=P,bα,则与b不平行C.,则a∥αD.∥α,b∥α,则∥b3.直线∥平面α,P∈α,过点P平行于的直线()A.只有一条,不在平面α内B.有无数条,不一定在α内C.只有一条,且在平面α内D.有无数条,一定在α内4.下列命题错误的是()A.平行于同一条直线的两个平面平行或相交B.平行于同一个平面的两个平面平行C.平行于同一条直线的两条直线平行D.平行于同一个平面的两条直线平行或相交5.平行四边形EFGH的四个顶点E、F、G、H、分别在空间四边形ABCD的四条边AB、BC、CD、AD...