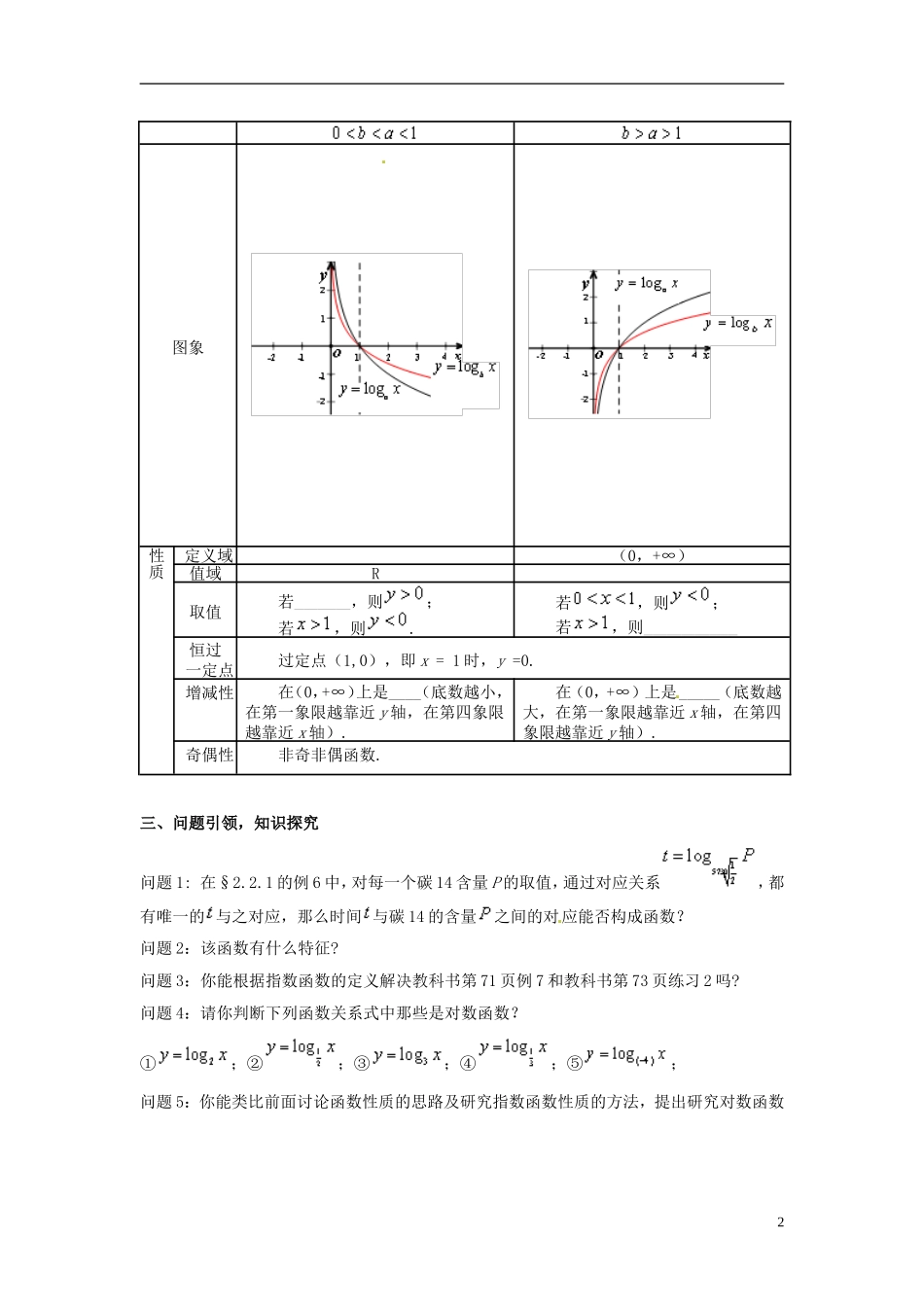
云南省德宏州芒市第一中学高中数学2.2.2第1课时对数函数的图像及性质教学设计新人教版必修1一、教学目标:(1)理解对数函数的性质,掌握对数函数的图像和性质;(2)掌握运用对数函数的单调性比较两个数的大小;了解对数函数在实际生活中的运用;理解同底的对数函数与指数函数互为反函数;(3)注重函数思想,等价转化、分类讨论等思想的渗透,提高数学建模能力。教学重点:本节内容是在学习了对数的概念与运算性质后,进一步学习对数函数的定义、图象、性质及初步应用;教学难点:突破难点的关键在于认识底数对函数值变化的影响。二、预习导学知识梳理1、对数函数定义:__________________________________________2、对数函数的图像及性质1三、问题引领,知识探究问题1:在§2.2.1的例6中,对每一个碳14含量P的取值,通过对应关系,都有唯一的与之对应,那么时间与碳14的含量之间的对应能否构成函数?问题2:该函数有什么特征?问题3:你能根据指数函数的定义解决教科书第71页例7和教科书第73页练习2吗?问题4:请你判断下列函数关系式中那些是对数函数?①;②;③;④;⑤;问题5:你能类比前面讨论函数性质的思路及研究指数函数性质的方法,提出研究对数函数图象性质定义域(0,+∞)值域R取值若____________,则;若,则.若,则;若,则____________________恒过一定点过定点(1,0),即x=1时,y=0.增减性在(0,+∞)上是____(底数越小,在第一象限越靠近y轴,在第四象限越靠近x轴).在(0,+∞)上是_____(底数越大,在第一象限越靠近x轴,在第四象限越靠近y轴).奇偶性非奇非偶函数.2的性质的方法吗?如何画出对数函数和的图象吗?问题6:从画出的图象中你能发现函数的图象和函数的图象有什么关系?可否利用的图象画出的图象?问题7:你能利用对数函数的图象归纳出对数函数的性质吗?四、目标检测1.函数的定义域是()A.B.C.D.2.已知函数,若,则等于()A.B.C.D.3.若,则的取值范围为。4.求的值域。五、分层配餐A组1.函数的定义域是()A.B.C.D.2.函数的定义域为()A.B.C.D.3.函数的定义域为()A.B.C.D.34.函数的定义域是()A.B.C.D.5.设函数的定义域为,函数的定义域为,则()A.是的真子集B.是的真子集C.D.6.函数的图像一定经过点()A.B.C.D.7.函数的值域是()A.B.C.D.8.函数的定义域是()A.B.C.D.B组9.函数的定义域为()A.B.C.D.10.设函数,则的值是()4A.B.C.D.11.设,函数在区间上的最大值与最小值之差为,则()A.B.C.D.12.函数的单调递增区间是()A.B.C.D.13.当时函数(1)与(2)在区间上的单调性为()A.都是增函数B.都是减函数C.(1)是增函数,(2)是减函数D.(2)是增函数,(1)是减函数C组14.设函数,若,则的取值范围是()A.B.C.D.15.函数在区间上的最大值比最小值大1,则。5