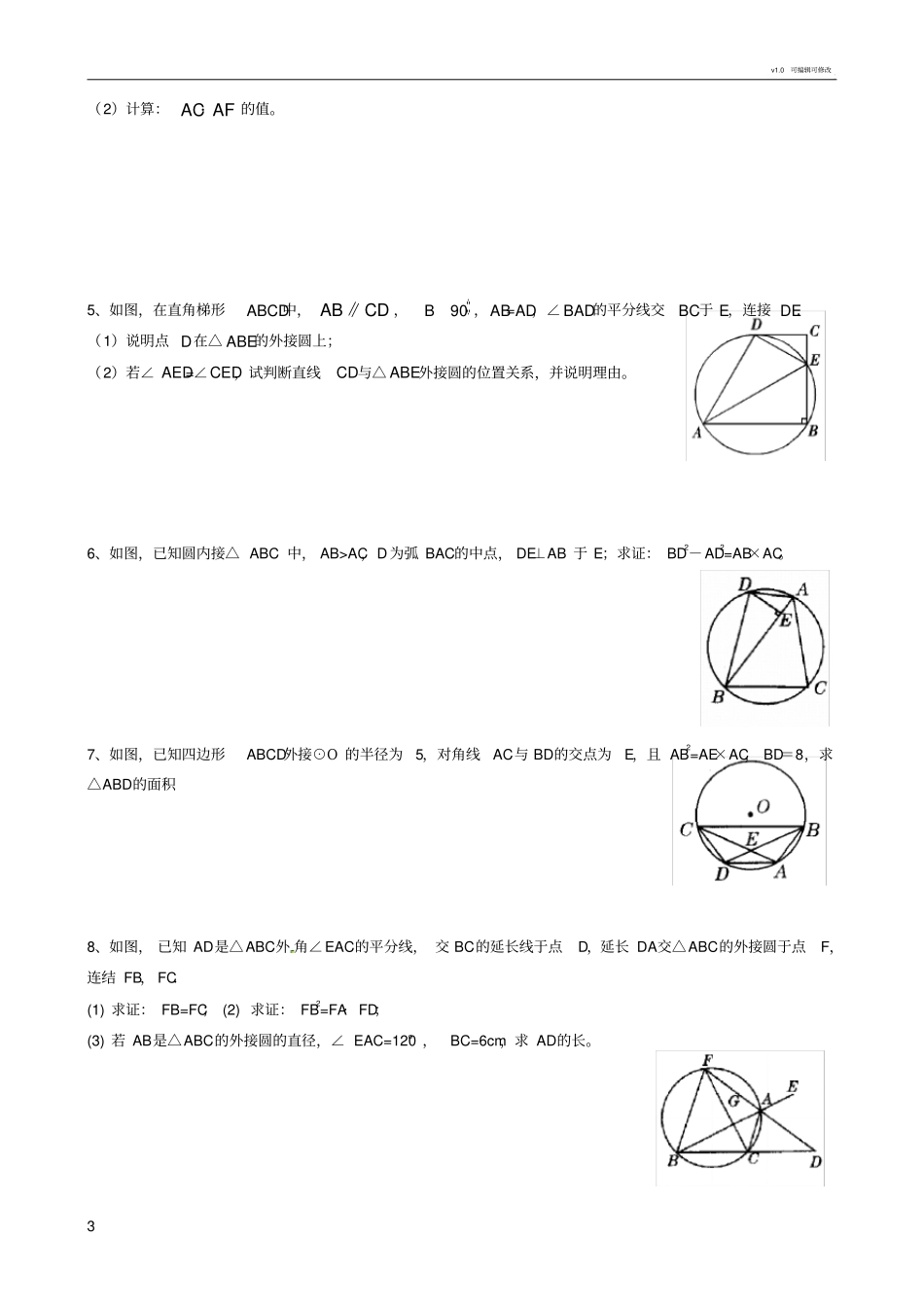
v1.0可编辑可修改1九年级圆中三角形相似复习专题1、黄金分割点:在线段AB上,点C把线段AB分成两条线段AC和BC(AC>BC),如果ACBCABAC,即AC2=AB×BC,那么称线段AB被点C黄金分割,点C叫做线段AB的黄金分割点,AC与AB的比叫做黄金比。其中ABAC215≈AB。2、黄金分割的几何作图:已知:线段AB.求作:点C使C是线段AB的黄金分割点.作法:(1)过点B作BD⊥AB,使BD=;(2)连结AD,在DA上截取DE=DB;(3)在AB上截取AC=AE,则点C就是所求作的线段AB的黄金分割点。(4)矩形中,如果宽与长的比是黄金比,这个矩形叫做黄金矩形3、相似三角形1)定义:如果两个三角形中,三角对应相等,三边对应成比例,那么这两个三角形叫做相似三角形。几种特殊三角形的相似关系:两个全等三角形一定相似。两个等腰直角三角形一定相似。两个等边三角形一定相似。两个直角三角形和两个等腰三角形不一定相似。补充:对于多边形而言,所有圆相似;所有正多边形相似(如正四边形、正五边形等等);4、性质:两个相似三角形中,对应角相等、对应边成比例。5、相似比:两个相似三角形的对应边的比,叫做这两个三角形的相似比。如△ABC与△DEF相似,记作△ABC∽△DEF。相似比为k。6、判定:①定义法:对应角相等,对应边成比例的两个三角形相似。②三角形相似的预备定理:平行于三角形一边的直线和其它两边相交,所构成的三角形与原三角形相似。三角形相似的判定定理:判定定理1:如果一个三角形的两个角与另一个三角形的两个角对应相等,那么这两个三角形相似.简述为:两角对应相等,两三角形相似。(此定理用的最多)判定定理2:如果一个三角形的两条边和另一个三角形的两条边对应成比例,并且夹角相等,那么这两个三角形相似.简述为:两边对应成比例且夹角相等,两三角形相似。判定定理3:如果一个三角形的三条边与另一个三角形的三条边对应成比例,那么这两个三角形相似;简述为:三边对应成比例,两三角形相似。7、直角三角形相似判定定理:(1)斜边与一条直角边对应成比例的两直角三角形相似。(2)直角三角形被斜边上的高分成的两个直角三角形与原直角三角形相似,并且分成的两个直角三角形也相似。v1.0可编辑可修改2题型:圆与三角形相似问题。1、如图,正方形ABCD内接于⊙O,点P在劣弧AB上,连结DP,交AC于点Q,若QP=QO,则QAQC的值为()A.132B.32C.23D.232、如图,已知点A、B、C、D顺次在⊙O上,ABBD,BM⊥AC于M,求证:AM=DC+CM。3、如图,已知四边形ABCD内接于直径为3的圆O,对角线AC是直径,对角线AC和BD的交点为P,AB=BD,且PC=0.6,求四边形ABCD的周长。4、如图,在RtABC△中,斜边1230BCC,°,D为BC的中点,ABD△的外接圆O⊙与AC交于F点,过A作O⊙的切线AE交DF的延长线于E点;(1)求证:AEDE⊥;QOPDCBAAEFODBCv1.0可编辑可修改3(2)计算:ACAF·的值。5、如图,在直角梯形ABCD中,ABCD∥,90B,AB=AD,∠BAD的平分线交BC于E,连接DE.(1)说明点D在△ABE的外接圆上;(2)若∠AED=∠CED,试判断直线CD与△ABE外接圆的位置关系,并说明理由。6、如图,已知圆内接△ABC中,AB>AC,D为弧BAC的中点,DE⊥AB于E;求证:BD2-AD2=AB×AC。7、如图,已知四边形ABCD外接⊙O的半径为5,对角线AC与BD的交点为E,且AB2=AE×AC,BD=8,求△ABD的面积8、如图,已知AD是△ABC外角∠EAC的平分线,交BC的延长线于点D,延长DA交△ABC的外接圆于点F,连结FB,FC.(1)求证:FB=FC;(2)求证:FB2=FA·FD;(3)若AB是△ABC的外接圆的直径,∠EAC=120°,BC=6cm,求AD的长。v1.0可编辑可修改49、如图,已知P是⊙O直径AB延长线上的一点,直线PCD交⊙O于C、D两点,弦DF⊥AB于点H,CF交AB于点E;(1)求证:PA·PB=PO·PE;(2)若DE⊥CF,∠P=15°,⊙O的半径为2,求弦CF的长。10、如图,AB,AC,AD是圆中的三条弦,点E在AD上,且AB=AC=AE.请你说明以下各式成立的理由:(1)∠CAD=2∠DBE;(2)AD2-AB2=BD·DC。11、如图所示,ABCD为☉O的内接四边形,E是BD上的一点,且有∠BAE=∠DAC;(1)求证:△ABC∽△AED;(2)求证:AB?DC+AD?BC=AC?BD。题型:动点问题。1、如图,在直角梯形ABCD中,AD∥BC,∠B=90°,AD=24...