第二章 原子的量子态(2)VIP免费

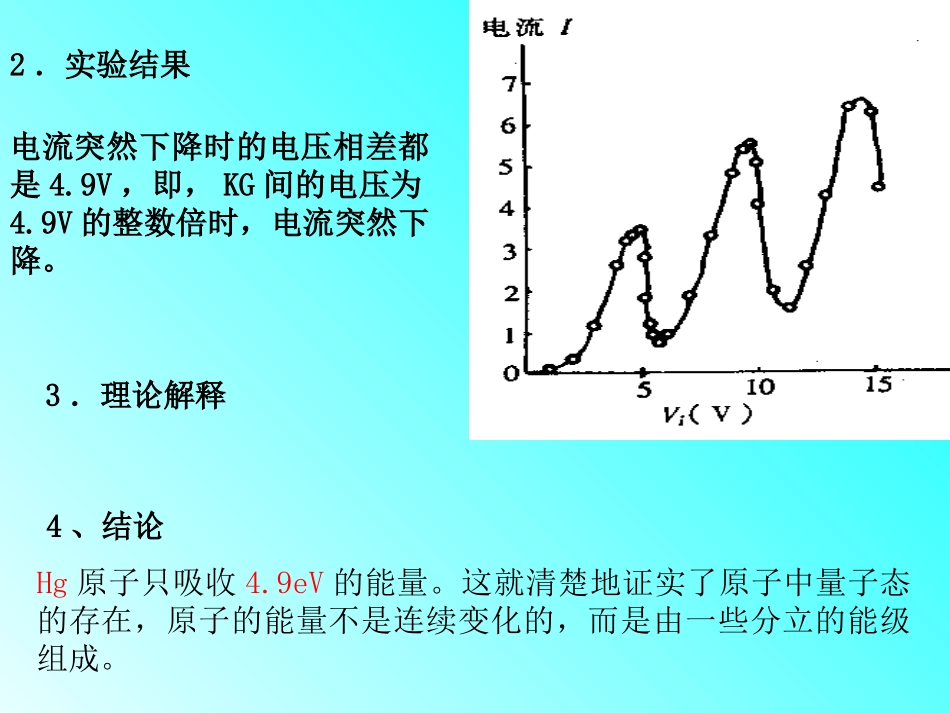
§2.4实验验证之二：夫兰克-赫兹实验一、原子与其它粒子的碰撞（1）弹性碰撞当两粒子碰撞时，只有粒子动能的交换，内能不变。产生条件：碰撞粒子动能较小（2）非弹性碰撞当两粒子碰撞时，粒子内部的能量有变化。第一类非弹性碰撞一部分能量转变内部能量，使原子或分子被激发产生条件：碰撞粒子的动能比较大第二类非弹性碰撞碰撞时，原子或分子的内部能量降低，放出的能量转变为动能产生条件：两粒子动能不大，且有一个原子处在高能态粒子的碰撞满足能量守恒和动量守恒原理二、夫兰克-赫兹实验1．实验装置(汞蒸汽)1914年，夫兰克（J.Frank）和赫兹（G.Hertz）用慢电子与稀薄气体原子碰撞的方法，使原子从低能级激发到较高能级。通过测量电子和原子碰撞时交换某一定值的能量，直接证明了原子内部量子化能级的存在。2．实验结果电流突然下降时的电压相差都是4.9V，即，KG间的电压为4.9V的整数倍时，电流突然下降。3．理论解释Hg原子只吸收4.9eV的能量。这就清楚地证实了原子中量子态的存在，原子的能量不是连续变化的，而是由一些分立的能级组成。4、结论4.9eV是不是Hg原子的第一激发态与基态之间的能级之差呢？12/~EEhchchnmEEhc6.253)/(12Hg原子的第一激发电势为4.9V。为什么更高的激发态未能得到激发？三、改进夫兰克-赫兹实验（1920）实验结果显示:原子被激发到不同的状态时，它所吸收的能量是不连续的。即原子体系的内部能量是量子化的。当＝4.68，4.9，5.29，5.78，6.73V时，下降。1KGUAI亚稳态？§2.5玻尔理论的推广1916年，德国人索末菲（sommerfeld）对Bohr理论作了进一步的发展。他认为在质点动力学中，有心力场中的质点运动轨迹一般来说是一个椭圆，因此，在库仑引力的作用下（有心力场）的电子，一般也应作椭圆运动，也就是说，索末菲将电子的定态轨道从圆轨道推广到椭圆轨道，进而把量子化条件给推广了。一、量子化条件的推广1916年，Summerfeld、Wilson(威尔逊)等人各自独立推广了玻尔的量子化条件，提出：对于每一个自由度，都必须分别满足量子化条件（也就是说，每一个自由度都应该有一个量子化条件）即hndqPiii其中代表自由度，为第个自由度的广义动量，为第个自由度的广义坐标，为第个自由度的量子数，按广义坐标q做一个周期的积分。iiiiiPiqin推广后的量子化条件包含了圆轨道的量子化条件。例：对于圆周运动，自由极角随时间作周期性变化，r为常量，即只有一个自由度，故只有一个量子化条件：hndqP3,2,1n在有心力场中，角动量是守恒量，故nhP2——玻尔的量子化条件二．椭圆轨道量子化对于椭圆轨道，原子核处在椭圆的一个焦点上，电子绕原子核作二维运动，即有两个自由度，故应有两个量子化条件。取平面极坐标（x,），这两个坐标对应的动量分别为动量和角动量，代入Sommerfeld量子化条件：rPPhndrPrr（1）hndP（2）其中和分别称为径量子数和角量子数。rnn由于电子在有心力场中运动，角动量是守恒量。由(2)式可得出PnP对（1），积分应遍及r的整个变化范围，经过计算可得：nnnnnbarZanZmehnnar122220244)(ZannZmehnnnbr1222044)(3,2,1nnnnnnr＝nn321，，三、能量量子化rZerrmVTE022224)(21椭圆轨道也是量子化的，它的长，短半轴之比必须是两个正整数之比；半长轴a只决定于与无关,所以相同的轨道,半长轴是相等的；半长轴b决定于和，可见椭圆的轨道是有一定形状的。nnnnn结论：把第一量子化积分时得出的结论,代入可得：2220242)4(2hnZmeE电子沿椭圆轨道运动时的总能量决定于轨道的半长轴a,即主量子数n,此时会有几个不同的半短轴b与之对应,这就是说,若能量一定,电子仍可以在几个不同的椭圆轨道上运动,象这种情况,我们成为简并。四、相对论修正Bohr曾提出,电子在原子的运动速度很大,故电子质量会发生相对论变化,从而影响原子各状态的能量。Summerfeld从理论上证明了若考虑相对论修正,对于氢和类氢原子，对于同一个，而不同的轨道的能量也不是严格相等,即不存在简并。nn根据...