温度应力、装配应力VIP免费

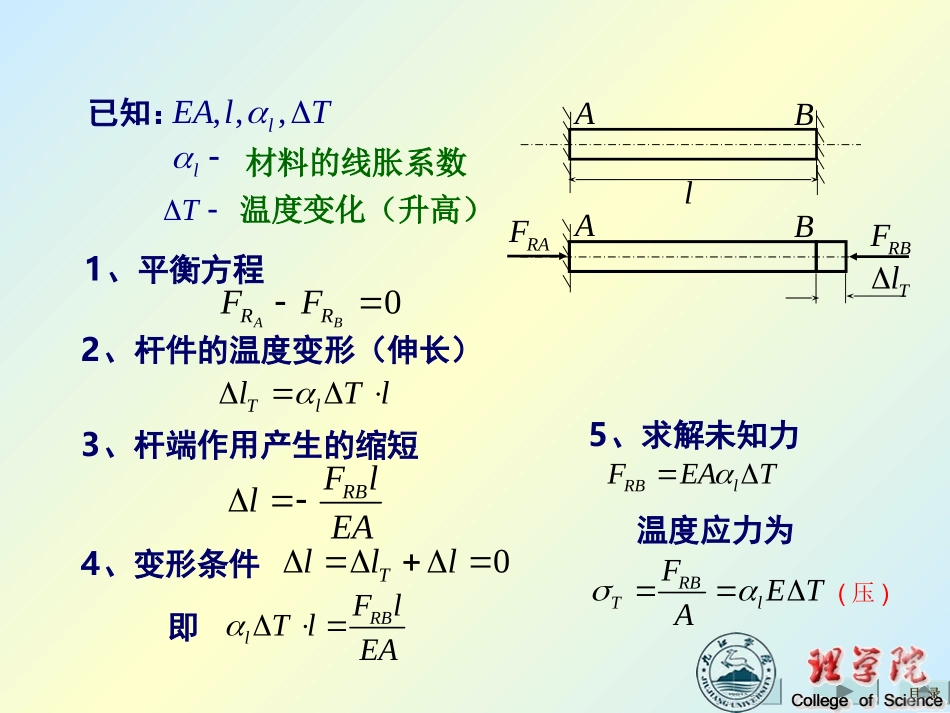
§2.11温度应力和装配应力一、温度应力温度应力——在超静定结构中，由于温度变化引起的变形受到约束的限制，因此在杆内将产生内力和应力，称为温度应力和热应力。此时杆件的变形——由温度变化引起的变形温度内力引起的弹性变形已知：,,,lEAlTl材料的线胀系数T温度变化（升高）2、杆件的温度变形（伸长）TllTl3、杆端作用产生的缩短RBFllEA4、变形条件0Tlll5、求解未知力RBlFEATRBTlFETARBlFlTlEA即温度应力为目录目录ABlABRBFTlRAF0BARRFF1、平衡方程(压)温度应力为：TET对于碳钢：所以GPa,/.2001105126ECMPa.TT52当较大时,温度应力的数值便非常可观。T二、装配应力装配应力——在超静定结构中，由于制造、装配不准确，在结构装配好后不受外力作用即已存在的应力。例两端用刚性块连接在一起的两根相同的钢杆1、2（图a），其长度l=200mm，直径d=10mm。求将长度为200.11mm，亦即e=0.11mm的铜杆3（图b）装配在与杆1和杆2对称的位置后（图c）各杆横截面上的应力。已知：铜杆3的横截面为20mm×30mm的矩形，钢的弹性模量E=210GPa，铜的弹性模量E3=100GPa。(d)解：0201NN3FFFx，变形协调方程（图c）为ell31利用物理关系得补充方程：eAElFEAlF33N3N1将补充方程与平衡方程联立求解得：EAAElAeEFAEEAleEAFF21121133333N332NN1，各杆横截面上的装配应力如下：（压）拉MPa51.19)(MPa53.743N331N21AFAF应力集中：由于杆件外形突然变化而引起局部应力急剧增大的现象。理论应力集中因数：§2.12应力集中的概念maxK截面尺寸改变越急剧，角越尖，孔越小，应力集中的程度越严重。在构件上开孔、开槽时采用圆形、椭圆或带圆角的，避免或禁开方形及带尖角的孔槽，在截面改变处尽量采用光滑连接等。（a）静载荷作用下：塑性材料所制成的构件对应力集中的敏感程度较小；脆性材料所制成的构件必须要考虑应力集中的影响。即当达到时，该处首先产生破坏。maxbFb（b）动载荷作用下：无论是塑性材料制成的构件还是脆性材料所制成的构件都必须要考虑应力集中的影响。一.剪切的实用计算§2-13剪切和挤压的实用计算铆钉连接剪床剪钢板FF目录目录nnn-n，剪切面销轴连接剪切受力特点：作用在构件两侧面上的外力合力大小相等、方向相反且作用线很近。变形特点：位于两力之间的截面发生相对错动。FF目录目录FFFFmmFSFmmSFmmFFnnFFsnFnFsnnF｛｛｝2F2FF｝FsFsnnFmmFFsFFsFF2sFF剪力假设切应力在剪切面（m-m截面）上是均匀分布的,得实用切应力计算公式：AFs切应力强度条件：AFs许用切应力，常由实验方法确定塑性材料：7.05.0脆性材料：0.18.0目录目录二.挤压的实用计算FF压溃(塑性变形)FF挤压面①接触面为平面，计算挤压面就是该面②接触面为弧面，取受力面对直径的投影面bsbsbsAF挤压力挤压面tdFbsAbs=td塑性材料：5.25.1bs脆性材料：5.19.0bsbsbsbsbsAF挤压强度条件：bs许用挤压应力，常由实验方法确定目录目录电瓶车挂钩由插销联接，如图示。插销材料为20钢，[τ]=30MPa，[σbs]＝100MPa，直径d=20mm。挂钩及被联接的板件的厚度分别为t=8mm和1.5t=12mm。牵引力F=15kN。试校核插销的强度。AFSMPa9.231020210154242332SdFAFbs333bsbsbsMPa5.621020101210155.1dtFAFbsbsbsbsAF平键连接图示齿轮用平键与轴连接，已知轴的直径d=70mm，键的尺寸为，传递的扭转力偶矩Me=2kN·m，键的许用应力[τ]=60MPa，[]=100MPa。试校核键的强度。mmlhb1001220bsOFdMe｝nnhb(a)FSMennO(b)0.5hbsbsbsAFFSnnbl(c)目录目录解：（1）校核键的剪切强度sFAbl由平衡方程0oM得22seddFblM6922200028.61028.6[]201007010eMPaMPabld（2）校核键的挤压强度2bsbsbsbshFAl由平衡方程得sbsFF或2bshbll366322(2010)(28.610)95.31095.3[]1210bsbsbPaMPah平键满足强度要求。目录目录