上海交大大学物理习题5VIP免费

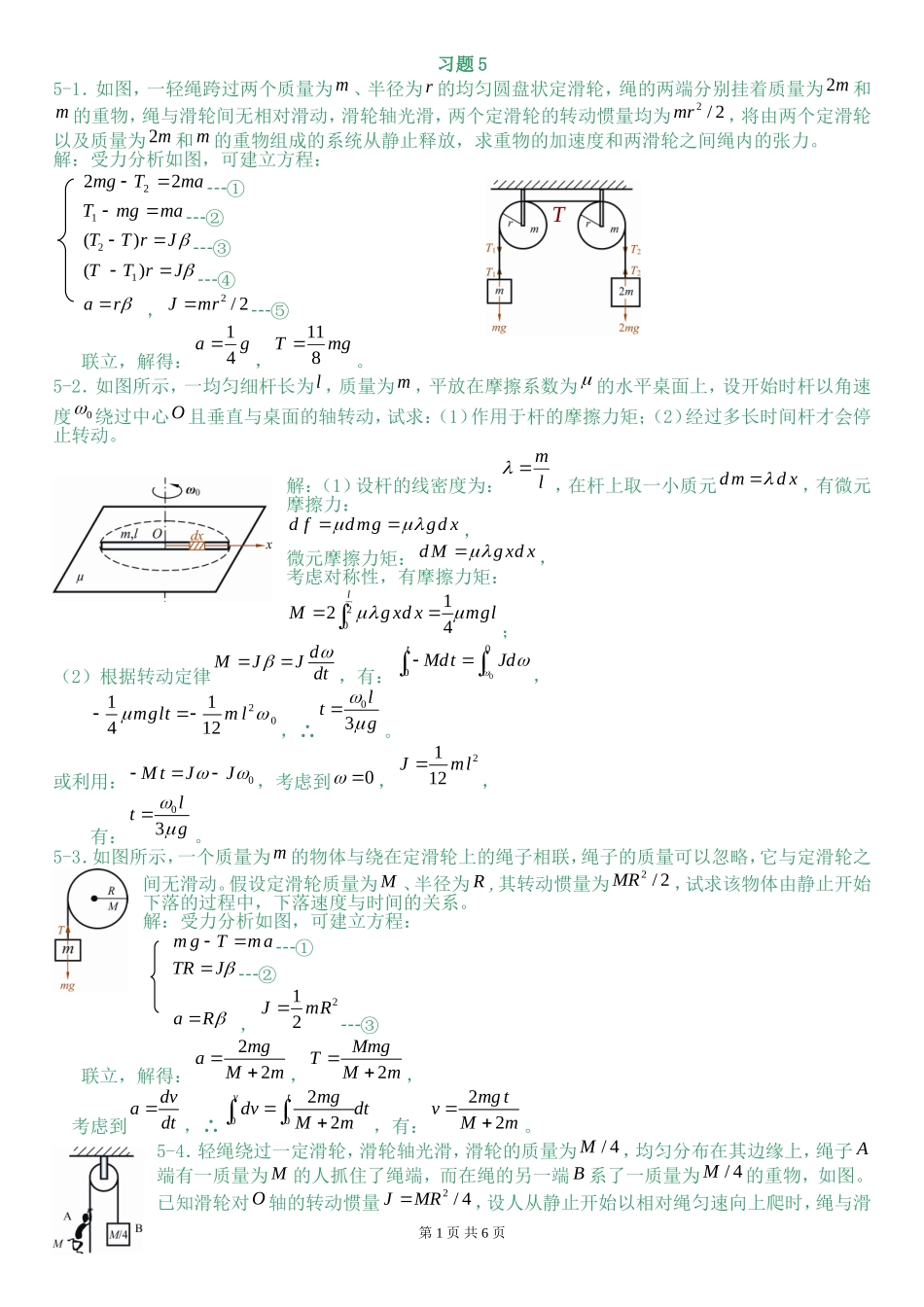
习题55-1．如图，一轻绳跨过两个质量为m、半径为r的均匀圆盘状定滑轮，绳的两端分别挂着质量为m2和m的重物，绳与滑轮间无相对滑动，滑轮轴光滑，两个定滑轮的转动惯量均为2/2mr，将由两个定滑轮以及质量为m2和m的重物组成的系统从静止释放，求重物的加速度和两滑轮之间绳内的张力。解：受力分析如图，可建立方程：maTmg222┄①mamgT1┄②2()TTrJ┄③JrTT)(1┄④ra，2/2Jmr┄⑤联立，解得：ga41，mgT811。5-2．如图所示，一均匀细杆长为l，质量为m，平放在摩擦系数为的水平桌面上，设开始时杆以角速度0绕过中心O且垂直与桌面的轴转动，试求：（1）作用于杆的摩擦力矩；（2）经过多长时间杆才会停止转动。解：（1）设杆的线密度为：lm，在杆上取一小质元dmdx，有微元摩擦力：dfdmggdx，微元摩擦力矩：dMgxdx，考虑对称性，有摩擦力矩：20124lMgxdxmgl；（2）根据转动定律dMJJdt，有：000tMdtJd，2011412mgltml，∴03ltg。或利用：0MtJJ，考虑到0，2112Jml，有：03ltg。5-3．如图所示，一个质量为m的物体与绕在定滑轮上的绳子相联，绳子的质量可以忽略，它与定滑轮之间无滑动。假设定滑轮质量为M、半径为R,其转动惯量为2/2MR，试求该物体由静止开始下落的过程中，下落速度与时间的关系。解：受力分析如图，可建立方程：mgTma┄①JTR┄②aR，212JmR┄③联立，解得：22mgaMm，2MmgTMm，考虑到dvadt，∴0022vtmgdvdtMm，有：22mgtvMm。5-4．轻绳绕过一定滑轮，滑轮轴光滑，滑轮的质量为4/M，均匀分布在其边缘上，绳子A端有一质量为M的人抓住了绳端，而在绳的另一端B系了一质量为4/M的重物，如图。已知滑轮对O轴的转动惯量4/2MRJ，设人从静止开始以相对绳匀速向上爬时，绳与滑第1页共6页T轮间无相对滑动，求B端重物上升的加速度？解一：分别对人、滑轮与重物列出动力学方程AMaTMg1人BaMgMT442物JRTRT21滑轮由约束方程:RaaBA和4/2MRJ,解上述方程组得到2ga.解二：选人、滑轮与重物为系统，设u为人相对绳的速度，v为重物上升的速度，注意到u为匀速，0dudt，系统对轴的角动量为：213()()442MLMvRMuvRRMvRMuBAR()()体人(物物体)而力矩为：13M44MgRMgRMgR，根据角动量定理dtdLM有：)23(43MuRMvRdtdMgR，∴2ga。5-5．计算质量为m半径为R的均质球体绕其轴线的转动惯量。解：设球的半径为R，总重量为m，体密度334mR，考虑均质球体内一个微元：2sindmrdrdd，由定义：考虑微元到轴的距离为sinr2(sin)Jrdm，有：222000(sin)sinRJrrdrdd520012[(1cos)cos]5Rrd225mR。5-6．一轻弹簧与一均匀细棒连接，装置如图所示，已知弹簧的劲度系数40/kNm，当0时弹簧无形变，细棒的质量kg0.5m，求在0的位置上细棒至少应具有多大的角速度，才能转动到水平位置？解：以图示下方的三角桩为轴，从00~90时，考虑机械能守恒，那么：0时的机械能为：第2页共6页22()(2)1123lmgml（重力势能转动动能），090时的机械能为：212kx有：2221112232lmgmlkx（）根据几何关系：22215.1)5.0(x，得：128.3srad5-7．如图所示，一质量为m、半径为R的圆盘，可绕O轴在铅直面内转动。若盘自静止下落，略去轴承的摩擦，求：（1）盘到虚线所示的铅直位置时，质心C和盘缘A点的速率；（2）在虚线位置轴对圆盘的作用力。解：（1）设虚线位置的C点为重力势能的零点，下降过程机械能守恒，有：221JmgR，而2221322JmRmRmR∴Rg3434RgRvc1623ARgvR（2）273yFmgmRmg（重力）（向心力），方向向上。5-8．如图所示，长为l的轻杆，两端各固定质量分别为m和m2的小球，杆可绕水平光滑固定轴O在竖直面内转动，转轴O距两端分别为l31和l32．轻杆原来静止在竖直位置。今有一质量为m的小球，以水平速度0v与杆下端小球m作对心碰撞，碰后以021v的速度...