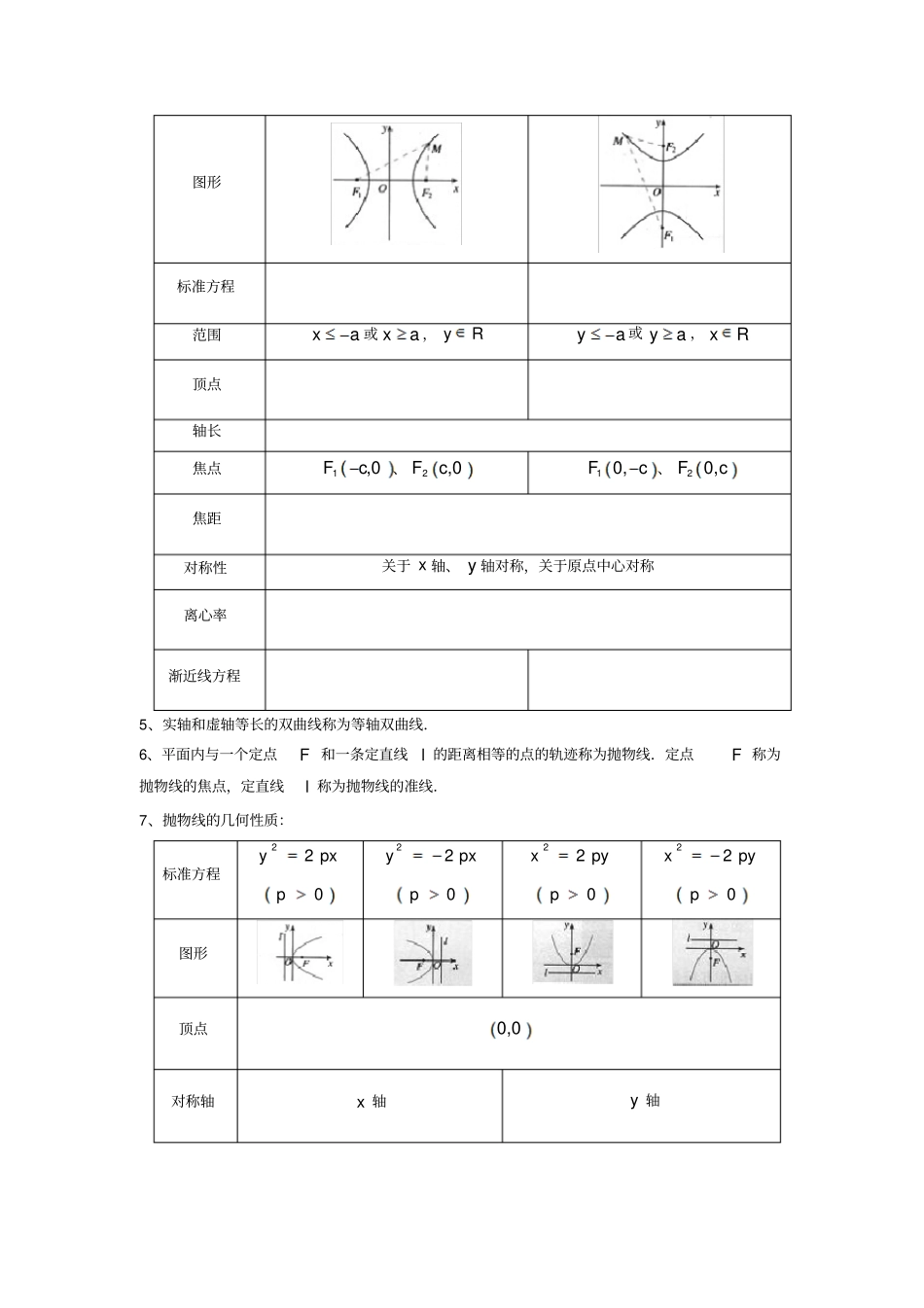
2.1.8圆锥曲线与方程(学案)一、知识梳理1、平面内与两个定点1F,2F的(大于12FF)的点的轨迹称为椭圆.即:|)|2(,2||||2121FFaaMFMF。这两个定点称为椭圆的焦点,两焦点的距离称为椭圆的.2、椭圆的几何性质:焦点的位置焦点在x轴上焦点在y轴上图形标准方程范围顶点轴长焦点1,0Fc、2,0Fc10,Fc、20,Fc焦距222122FFccab对称性关于x轴、y轴、原点对称离心率3、平面内与两个定点1F,2F的(小于12FF)的点的轨迹称为双曲线.即:|)|2(,2||||||2121FFaaMFMF。这两个定点称为双曲线的焦点,称为双曲线的焦距.4、双曲线的几何性质:焦点的位置焦点在x轴上焦点在y轴上图形标准方程范围xa或xa,yRya或ya,xR顶点轴长焦点1,0Fc、2,0Fc10,Fc、20,Fc焦距对称性关于x轴、y轴对称,关于原点中心对称离心率渐近线方程5、实轴和虚轴等长的双曲线称为等轴双曲线.6、平面内与一个定点F和一条定直线l的距离相等的点的轨迹称为抛物线.定点F称为抛物线的焦点,定直线l称为抛物线的准线.7、抛物线的几何性质:标准方程22ypx0p22ypx0p22xpy0p22xpy0p图形顶点0,0对称轴x轴y轴焦点准线方程离心率1e范围0x0x0y0y8、过抛物线的焦点作垂直于对称轴且交抛物线于、两点的线段,称为抛物线的“通径”,即2p.二、典例解析探究点一直线与圆锥曲线的位置关系判断例1、已知直线l:kx-y+2-k=0,双曲线C:x2-4y2=4,当k为何值时,(1)l与C无公共点;(2)l与C有唯一公共点;(3)l与C有两个不同的公共点.总结:判断直线l与圆锥曲线C的位置关系时,可将直线l的方程代入曲线C的方程,消去y(或x)得一个关于变量x(或y)的一元二次方程ax2+bx+c=0.(1)当a≠0时,若Δ>0,则直线l与曲线C相交;若Δ=0,则直线l与曲线C相切;若Δ<0,则直线l与曲线C相离.(2)当a=0时,即得到一个一次方程,则l与C相交,且只有一个交点.此时,若C为双曲线,则l平行于双曲线的渐近线;若C为抛物线,则l平行于抛物线的对称轴.(3)当直线与双曲线或抛物线只有一个公共点时,直线与双曲线或抛物线可能相切,也可能相交.探究点二相交弦长问题例2、已知椭圆的中心在坐标原点O,焦点在坐标轴上,直线y=x+1与椭圆交于P,Q两点,且OP⊥OQ,|PQ|=102,求椭圆的方程.总结:若直线l与圆锥曲线F(x,y)=0相交于A,B两点,求弦AB的长可用下列两种方法:(1)把直线的方程与圆锥曲线的方程联立,解得点A,B的坐标,然后用两点间距离公式,便得到弦AB的长,一般来说,这种方法较为麻烦.(2)不求交点坐标,可用一元二次方程根与系数的关系求解.设直线方程为y=kx+m,与圆锥曲线F(x,y)=0交于两点A(x1,y1),B(x2,y2),则|AB|=(x1-x2)2+(y1-y2)2=(x1-x2)2+(kx1+m-kx2-m)2=1+k2·(x1+x2)2-4x1x2;或当k≠0时,|AB|=1+1k2|y1-y2|=1+1k2·(y1+y2)2-4y1y2.当k=0时,直线平行于x轴,∴|AB|=|x1-x2|.探究三中点弦问题例3、已知椭圆x216+y24=1,求:(1)以P(2,-1)为中点的弦所在直线的方程;(2)斜率为2的平行弦中点的轨迹方程;(3)过Q(8,2)的直线被椭圆截得的弦的中点的轨迹方程.总结:对中点弦问题,常用的解题方法——平方差法,其解题步骤为:(1)设点,即设出弦的两端点坐标;(2)代入,即代入圆锥曲线方程;(3)作差,即两式相减,然后用平方差公式把上式展开,整理.三、当堂检测1.已知双曲线22221xyab的一个焦点与抛物线24yx的焦点重合,且双曲线的离心率等于5,则该双曲线的方程为()A.225514yxB.22154xyC.22154yxD.224515yx2.双曲线12222byax的离心率为3,则它的渐近线方程是()A.xy2B.xy22C.xy2D.xy213.以双曲线221124yx的顶点为焦点,长半轴长为4的椭圆方程为()A.2216452xyB.2211612xyC.221164xyD.221416xy4.过椭圆22221xyab(0ab)的左焦点1F作x轴的垂线交椭圆于点P,2F为右焦点,若1260FPF则椭圆的离心率为()A.22B.33C.12D.135.椭圆221259xy上一点M到左焦点1F的距离是2,N是1MF的中点,O为坐标原点,则ON.6.过双曲线22221(0,0)xyabab的右焦点F和虚轴端点B作一条直线,若右顶点A到直线FB的距离等于7b,则双曲线的离心率e7.抛物线yx22上与点)2,0(M距离最近的点的坐标是8.已知抛物线的顶点在原点,焦点为)0,3(F,设点)0,(aM与抛物线上的点的距离的最小值afd,求af的表达式。