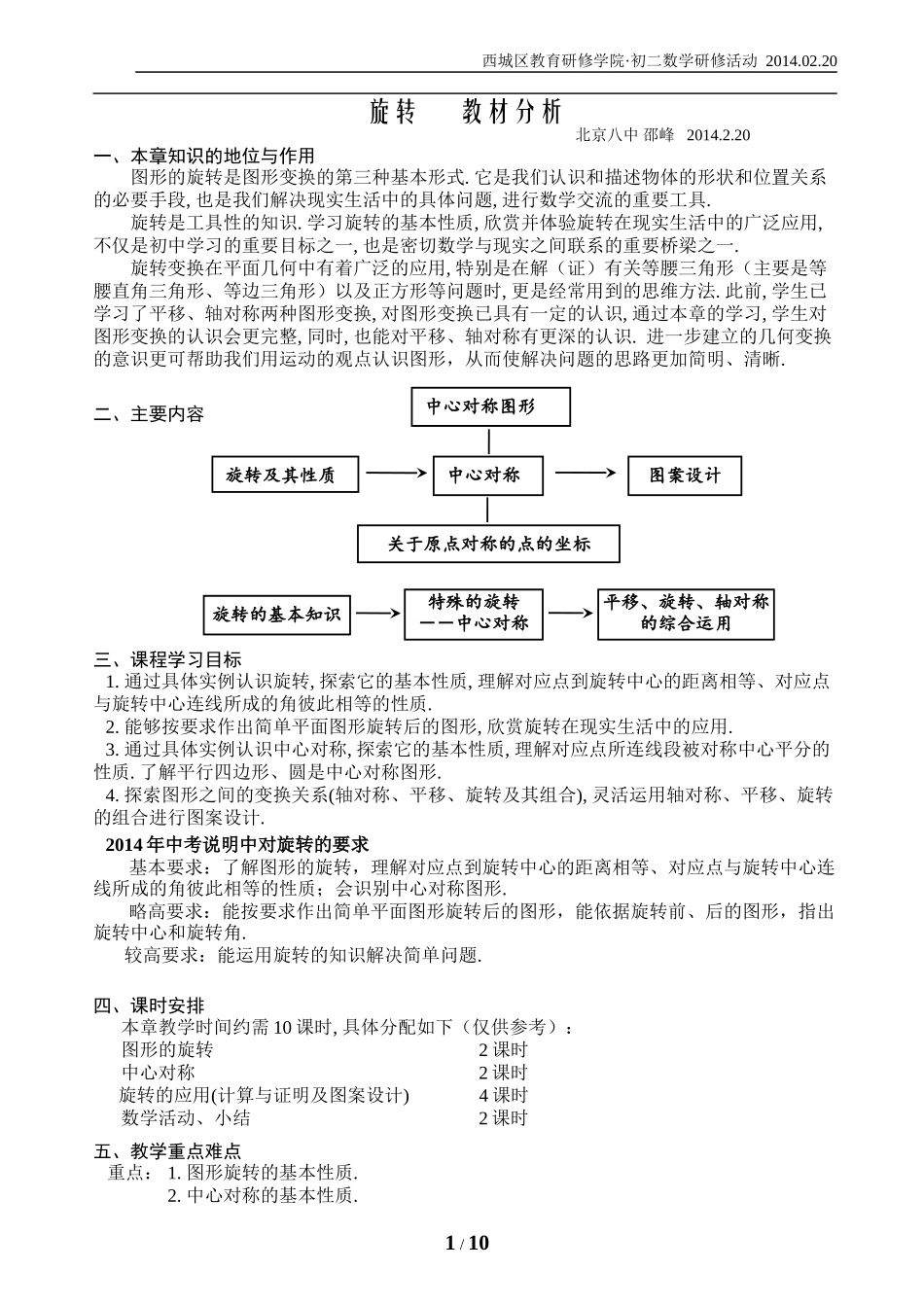
西城区教育研修学院·初二数学研修活动2014.02.20旋转教材分析北京八中邵峰2014.2.20一、本章知识的地位与作用图形的旋转是图形变换的第三种基本形式.它是我们认识和描述物体的形状和位置关系的必要手段,也是我们解决现实生活中的具体问题,进行数学交流的重要工具.旋转是工具性的知识.学习旋转的基本性质,欣赏并体验旋转在现实生活中的广泛应用,不仅是初中学习的重要目标之一,也是密切数学与现实之间联系的重要桥梁之一.旋转变换在平面几何中有着广泛的应用,特别是在解(证)有关等腰三角形(主要是等腰直角三角形、等边三角形)以及正方形等问题时,更是经常用到的思维方法.此前,学生已学习了平移、轴对称两种图形变换,对图形变换已具有一定的认识,通过本章的学习,学生对图形变换的认识会更完整,同时,也能对平移、轴对称有更深的认识.进一步建立的几何变换的意识更可帮助我们用运动的观点认识图形,从而使解决问题的思路更加简明、清晰.二、主要内容三、课程学习目标1.通过具体实例认识旋转,探索它的基本性质,理解对应点到旋转中心的距离相等、对应点与旋转中心连线所成的角彼此相等的性质.2.能够按要求作出简单平面图形旋转后的图形,欣赏旋转在现实生活中的应用.3.通过具体实例认识中心对称,探索它的基本性质,理解对应点所连线段被对称中心平分的性质.了解平行四边形、圆是中心对称图形.4.探索图形之间的变换关系(轴对称、平移、旋转及其组合),灵活运用轴对称、平移、旋转的组合进行图案设计.2014年中考说明中对旋转的要求基本要求:了解图形的旋转,理解对应点到旋转中心的距离相等、对应点与旋转中心连线所成的角彼此相等的性质;会识别中心对称图形.略高要求:能按要求作出简单平面图形旋转后的图形,能依据旋转前、后的图形,指出旋转中心和旋转角.较高要求:能运用旋转的知识解决简单问题.四、课时安排本章教学时间约需10课时,具体分配如下(仅供参考):图形的旋转2课时中心对称2课时旋转的应用(计算与证明及图案设计)4课时数学活动、小结2课时五、教学重点难点重点:1.图形旋转的基本性质.2.中心对称的基本性质.1/10旋转及其性质中心对称关于原点对称的点的坐标图案设计旋转的基本知识特殊的旋转--中心对称平移、旋转、轴对称的综合运用中心对称图形西城区教育研修学院·初二数学研修活动2014.02.203.两个点关于原点对称时,它们坐标之间的关系.难点:1.图形旋转的基本性质的归纳与运用.2.中心对称的基本性质的归纳与运用.六、整体教学建议:1、明确学习图形变换的大致思路⑴通过具体实例认识图形变换;⑵探索图形变换的性质;⑶依据图形变换的性质进行作图、计算和证明;⑷利用图形变换进行图案设计;⑸用坐标表示图形变换.2、注意联系实际旋转与现实生活联系紧密,为此,在教学中应列举了大量实例来使学生认识和感受它们,增强学生对旋转的理解.利用图形变换进行图案设计、解决实际问题又加强了图形变换与现实生活的联系.3、注意培养动手操作的意识教材在探索旋转的性质、中心对称的性质以及如何设计图案最美观等问题时,安排了转动硬纸板、转动三角板、转动模板等应用动手操作来探索结论的内容.动手操作是解决问题的一种方法,应加强学生主动进行动手操作的意识.4、注意概念之间的联系⑴平移、旋转、轴对称学习旋转变换与学习平移、轴对称的过程基本一致,主要都是研究变换过程中的不变量,是研究几何问题、发现几何结论的有效工具.平移、轴对称、旋转都是全等变换,只改变图形的位置,不改变图形的形状和大小.由于变换方式的不同,故变换前后具有各自的性质.平移轴对称旋转相同点都是全等变换,即变换前后的图形全等.不同点定义把一个图形沿某一方向移动一定距离的图形变换,叫~.把一个图形沿着某一条直线折叠的图形变换叫~.把一个图形绕着某一定点转动一个角度的图形变换叫~.图形要素平移方向平移距离对称轴旋转中心、旋转方向、旋转角度性质连接各组对应点的线段平行(或共线)且相等.任意一对对应点所连线段被对称轴垂直平分.对应点到旋转中心的距离相等;对应点与旋转中心所连线段的夹角等于旋转角.即:对应点与旋转中心连线所成的角彼此相等.⑵旋转与中心对称中心对称是一种特殊的旋...