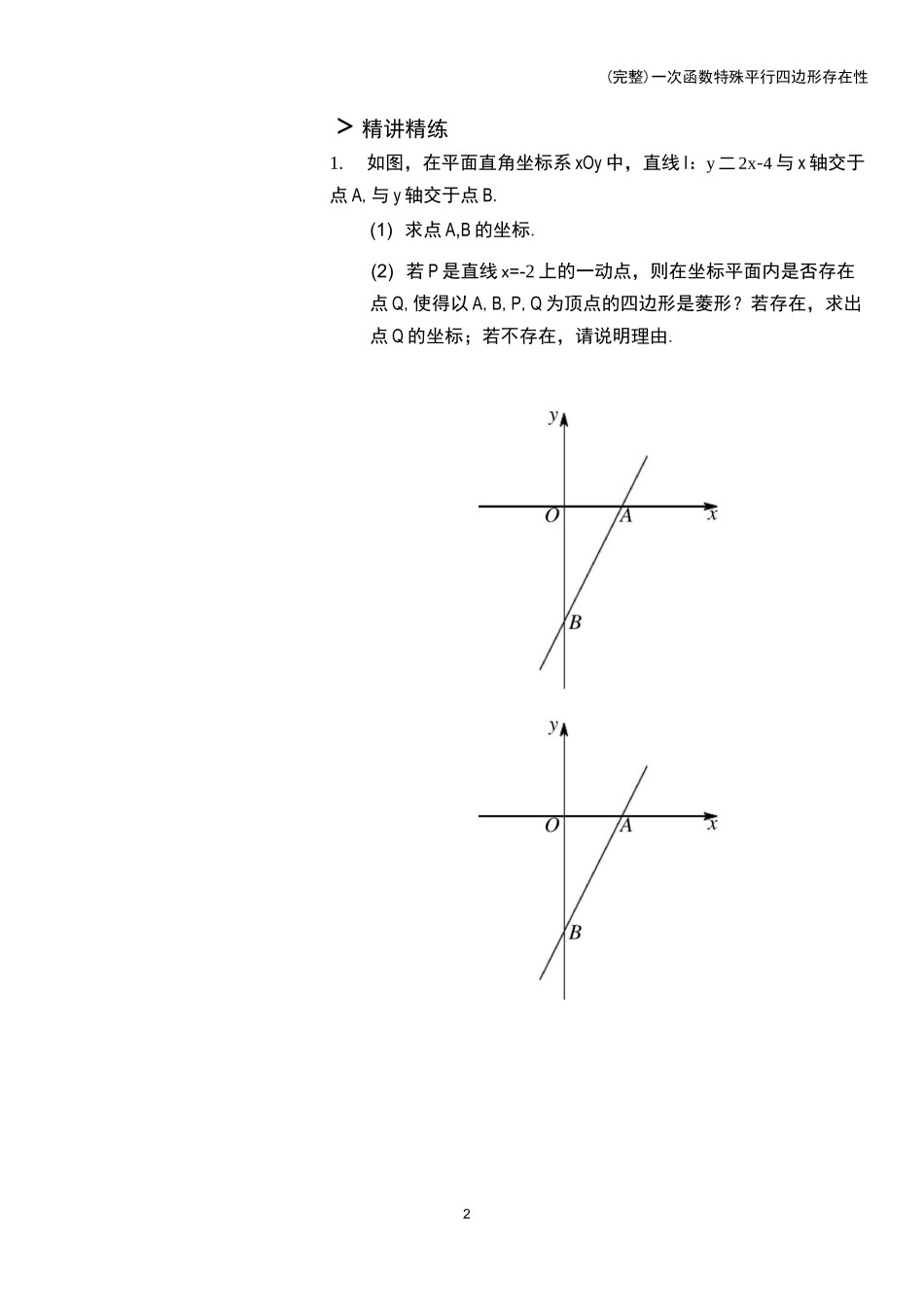
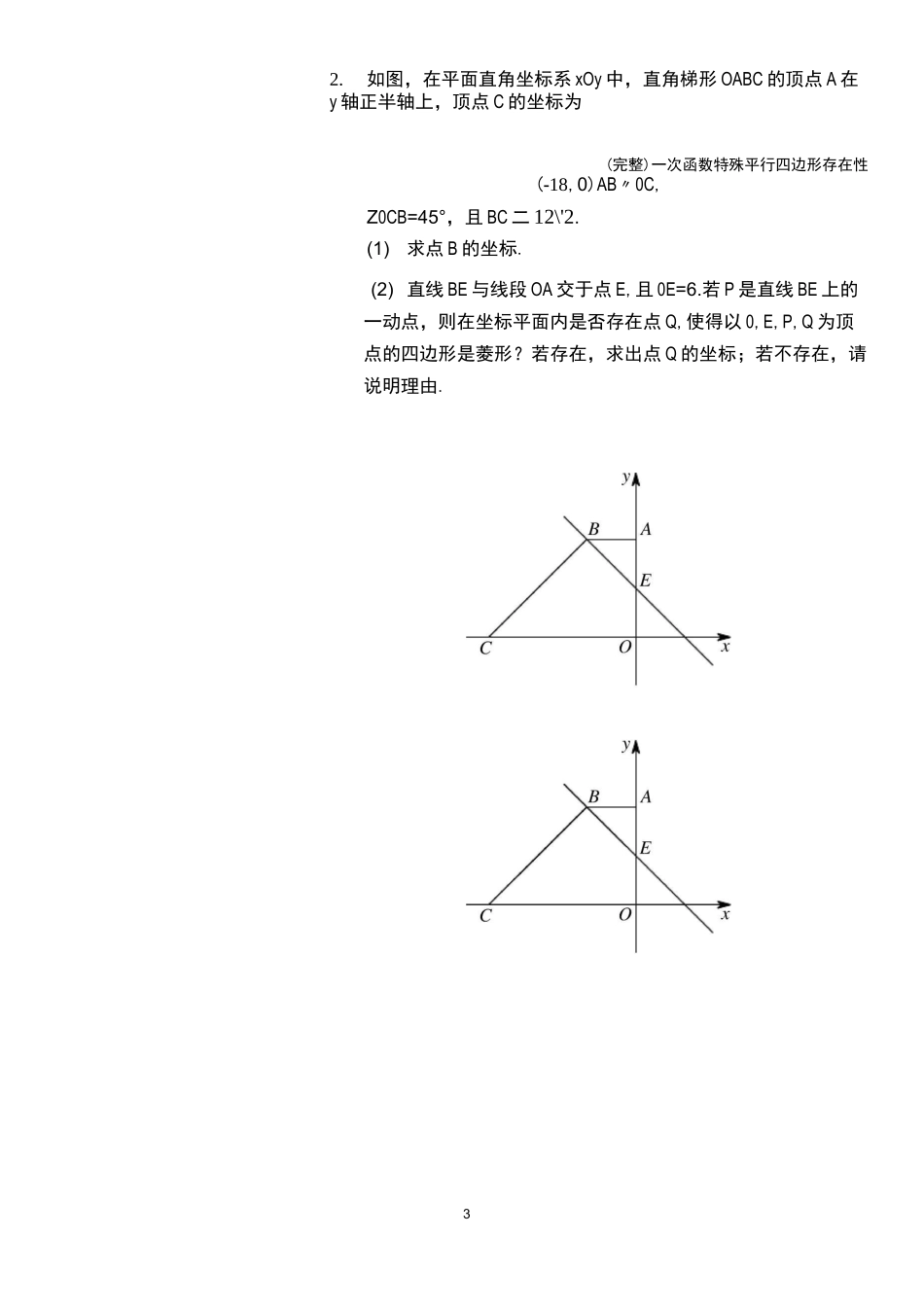
1特殊平行四边形存在性(完整)一次函数特殊平行四边形存在性>课前预习1.一般情况下我们如何处理存在性问题?(1)研究背景图形坐标系背景下研究、;几何图形研究(2)根据不变特征,确定分类标准研究定点,动点,定线段,确定分类标准不变特征举例:①等腰三角形(两定一动)以定线段作为或者来分类,利用确定点的位置.②等腰直角三角形(两定一动)以来分类,然后借助或者确定点的位置.(3)分析特殊状态的形成因素,画出符合题意的图形并求解(4)结果验证2.用铅笔做讲义第1,2题,并将计算、演草保留在讲义上,先看知识点睛,再做题,思路受阻时(某个点做了2〜3分钟)重复上述动作,若仍无法解决,课堂重点听.A知识点睛1.存在性问题处理框架:①研究背景图形.②根据不变特征,确定分类标准.③分析特殊状态的形成因素,画出符合题意的图形并求解.④结果验证.2.特殊平行四边形存在性问题不变特征举例:①菱形存在性问题(两定两动)转化为等腰三角形存在性问题;以定线段作为底边或者腰确定分类标准,利用两圆一线确定一动点的位置,然后通过平移确定另一动点坐标.②正方形存在性问题(两定两动)转化为等腰直角三角形存在性问题;根据直角顶点确定分类标准,利用两腰相等或者45°角确定一动点的位置,然后通过平移确定另一动点坐标.2(完整)一次函数特殊平行四边形存在性>精讲精练1.如图,在平面直角坐标系xOy中,直线I:y二2x-4与x轴交于点A,与y轴交于点B.(1)求点A,B的坐标.(2)若P是直线x=-2上的一动点,则在坐标平面内是否存在点Q,使得以A,B,P,Q为顶点的四边形是菱形?若存在,求出点Q的坐标;若不存在,请说明理由.32.如图,在平面直角坐标系xOy中,直角梯形OABC的顶点A在y轴正半轴上,顶点C的坐标为(完整)一次函数特殊平行四边形存在性(-18,0)AB〃0C,Z0CB=45°,且BC二12\'2.(1)求点B的坐标.(2)直线BE与线段OA交于点E,且0E=6.若P是直线BE上的一动点,则在坐标平面内是否存在点Q,使得以0,E,P,Q为顶点的四边形是菱形?若存在,求出点Q的坐标;若不存在,请说明理由.43.如图,在平面直角坐标系xOy中,DABCD的顶点A,B的坐标分别为A(0,3),B(-再,0),顶点C在x轴正半轴上,顶点D在第一象限,且AD二2爲.若M为坐标平面内一点,则在第一5(完整)一次函数特殊平行四边形存在性象限内是否存在点F,使得以A,C,F,M为顶点的四边形是正方形?若存在,求出点F的坐标;若不存在,请说明理由.4.如图,在平面直角坐标系中,已知点A,B,C的坐标分别为A(—9,0),B(16,0),C(0,12),D是线段BC上的一动点6(不与点B,C重合),过点D作直线DE丄0B,垂足为点E.若M为坐标平面内一点,则在直线DE上是否存在点N,使得以C,B,M,N为顶点的四边形是正方形?若存在,求出点N的坐标;若不存在,请说明理由.(完整)一次函数特殊平行四边形存在性5