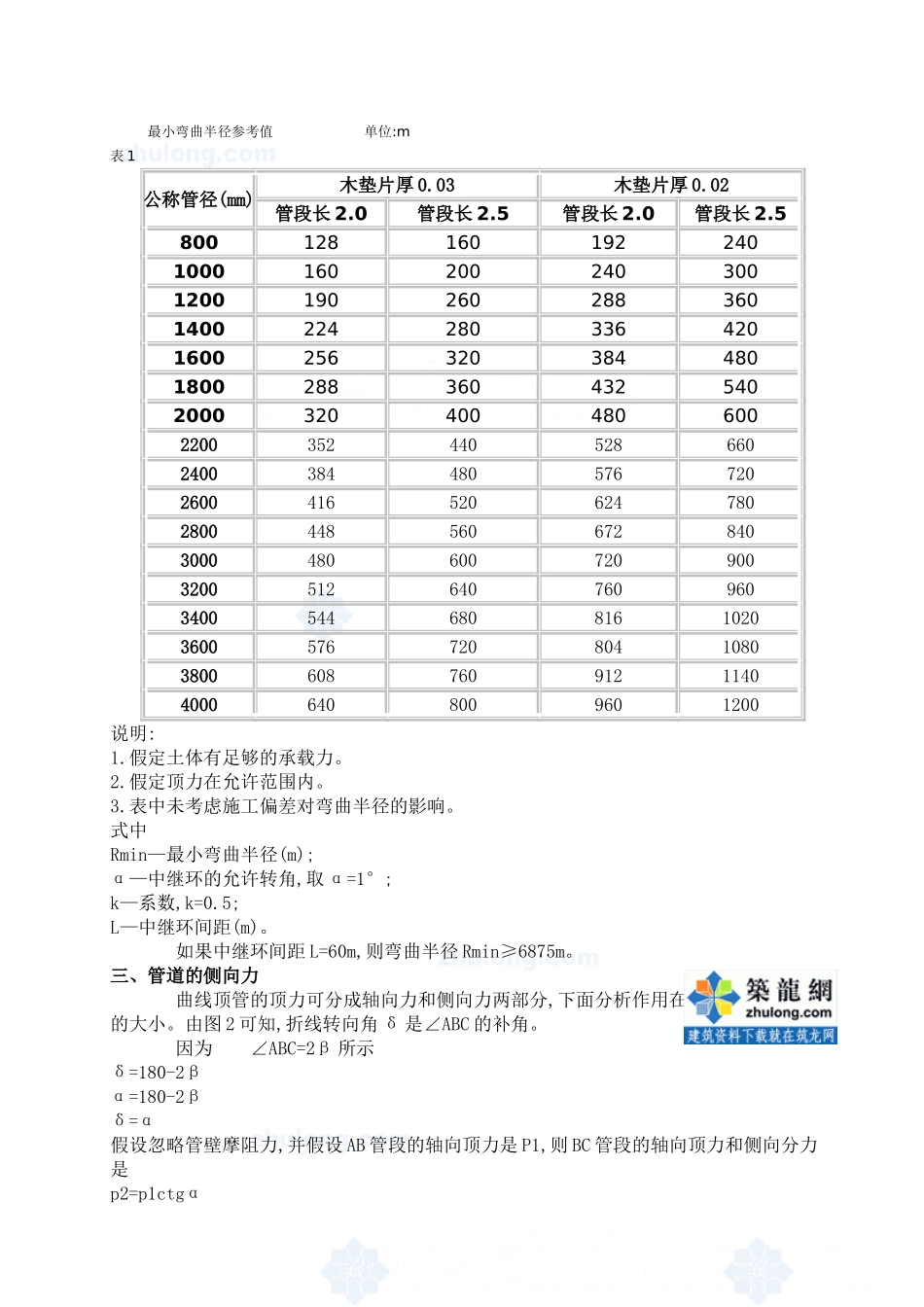
曲线顶管初探摘要本文对曲线顶管的最重要参数——最小曲线半径进行了探讨,得出最小曲线半径与管段长度、管径成正比,与木垫片厚度成反比的关系。另外还指出曲线半径还受土体承载力的制约,要防止管道在施工中发生纵向失稳。关键词顶管曲线顶管曲线顶管是顶管的前沿技术,只有当顶管被工程界广泛采纳后才会提出曲线顶管问题。目前曲线顶管各国尚处于研究发展阶段,有些曲线目前已能施工,有些曲线还不能。例如弯曲半径太小,有可能造成管道失稳,管道裂缝等严重后果。曲线顶管多用于旧城区的改造,旧城区马路弯曲,管道一般沿马路敷设,这就需要采用曲线顶管。另一种情况是过江过河的混凝土顶管,有时为了减少投资,把管轴线设计成倒虹管或者抛物线形状,这也需要采用曲线顶管。曲线顶管比较适合于混凝土管。曲线顶管用于钢管,则需要很大的弯曲半径,而且必须有中继环。管道的弯曲半径的大小与土质、管径、顶力有关。土体承载力高,弯曲半径可以小一点;反之,承载力低,弯曲半径要大一点。管道口径大,弯曲半径要大一点;反之,管道口径小,弯曲半径可以小一点。管段较长,弯曲半径要大一点;反之,管段较短,弯曲半径可以小一点。施工顶力较大,弯曲半径要大一点;反之,顶力较小,弯曲半径可以小一点。一、混凝土管最小弯曲半径分析最小弯曲半径时忽略土体承载力和施工顶力影响,仅就管道口径大小、管段长度、木垫片的厚度三者与最小弯曲半径的关系进行分析。曲线顶管的轴线,从宏观上看是曲线,实际上是折线,是多边形的一部份,多边形的边就是管段长度。从图1可知多边形的边、角、半径有如下关系:α=l/R式中α—中心角(弧度);l—边长;R—多边形外切圆半径。曲线顶管中把管段的长度看成是多边形的边,管段对应的中心角就是多边形的中心角,管轴线就是多边形的外切圆。假设管道内径为d,壁厚为t,管段长度为l,木垫片厚度为b,并假设管道壁厚是内径的1/10,木垫片允许最大压缩率是50%。即t=d/10S=b∙50%从图1可知,管段间的转角与管段对应的中心角相等。则曲线的最小弯曲半径可按下式计算:Rmin=l(d+2t)/(b-s)或Rmin=12ld/5b式中Rmin—最小弯曲半径(m);l—管段的长度(m);d—管道内径(m);t—管道壁厚(m);b—木垫片厚度(m);s—木垫片最小压缩高度(m)。由上式确定的不同管径混凝土管的最小弯曲半径见表1。弯曲半径太小,会使管段上应力过于集中,使管道混凝土裂缝。这是要力求避免的。二、钢管顶管的最小弯曲半径无中继环的钢管不能用于曲线顶管。钢管曲线顶管的最小弯曲半径的大小主要取决于中继环布置的间距和中继环的允许转角。目前钢管顶管沿用的老式中继环允许转角很小,因此不宜用于曲线顶管。组合密封中继环研究成功后,允许中继环有较大的转角,因此可用于曲线顶管。已知中继环的允许转角和间距,钢管管道的最小弯曲半径可按下式计算:Rmin≥L/2sin(kα/2)最小弯曲半径参考值单位:m表1公称管径(mm)木垫片厚0.03木垫片厚0.02管段长2.0管段长2.5管段长2.0管段长2.580012816019224010001602002403001200190260288360140022428033642016002563203844801800288360432540200032040048060022003524405286602400384480576720260041652062478028004485606728403000480600720900320051264076096034005446808161020360057672080410803800608760912114040006408009601200说明:1.假定土体有足够的承载力。2.假定顶力在允许范围内。3.表中未考虑施工偏差对弯曲半径的影响。式中Rmin—最小弯曲半径(m);α—中继环的允许转角,取α=1°;k—系数,k=0.5;L—中继环间距(m)。如果中继环间距L=60m,则弯曲半径Rmin≥6875m。三、管道的侧向力曲线顶管的顶力可分成轴向力和侧向力两部分,下面分析作用在管段上的侧向力的大小。由图2可知,折线转向角δ是∠ABC的补角。因为∠ABC=2β所示δ=180-2βα=180-2βδ=α假设忽略管壁摩阻力,并假设AB管段的轴向顶力是P1,则BC管段的轴向顶力和侧向分力是p2=p1ctgαp′2=p1tgα式中p2—下一管段的轴向顶力;p′2—下一管段的侧向分力。由此可见,曲线顶管存在侧向分力,因此要验算土体的承载力。如果承载力不够,管轴线会因此失稳,侧向分力使管道靠向曲线外侧,并作用在土体上,还会使管道的顶进阻力增加。因此曲线顶管在...