复数的概念及几何意义VIP免费

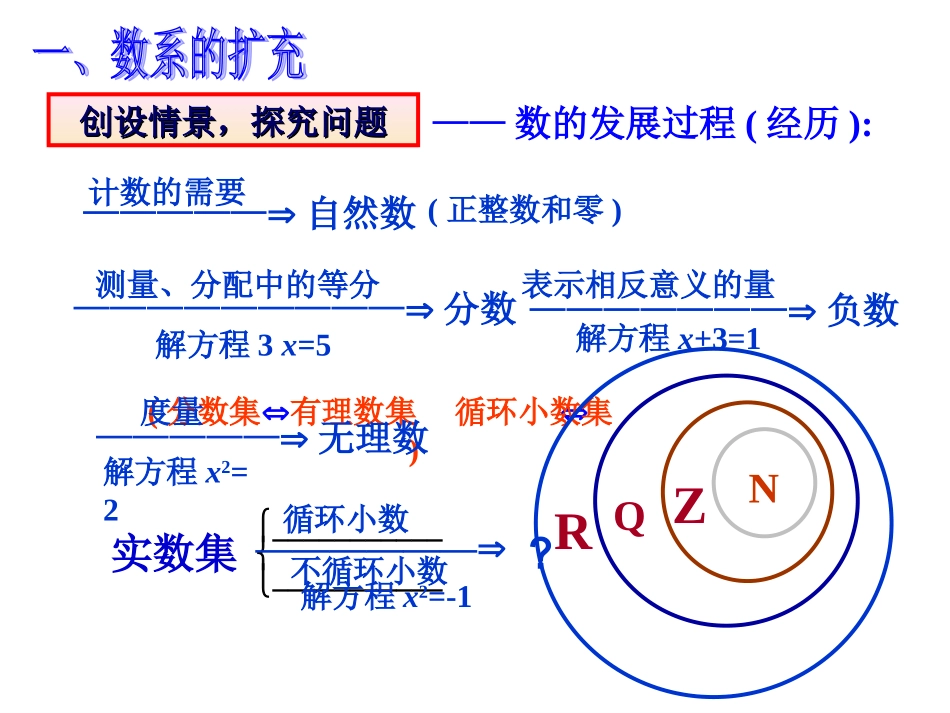
——数的发展过程(经历):—————自然数计数的需要(正整数和零)—————————分数表示相反意义的量解方程x+3=1———————负数测量、分配中的等分解方程3x=5(分数集)有理数集循环小数集—————无理数度量解方程x2=2实数集______________________循环小数不循环小数解方程x2=-1——————?创设情景，探究问题创设情景，探究问题NZQR合情推理，类比扩充合情推理，类比扩充我们能否将实数集进行扩充，使得在新的数集我们能否将实数集进行扩充，使得在新的数集中，该问题能得到圆满解决呢？中，该问题能得到圆满解决呢？引入一个新数：引入一个新数：i规定规定12x一元二次方程在实数集范围内无解引入新数，完善数系引入新数，完善数系（2）i可以与实数进行四则运算，且原有的加、乘运算律仍然成立.（1）i2＝－1；3.1复数的概念及几何意义复数有关概念复数有关概念1、定义:形如a+bi（aR∈，bR∈）的数叫复数,其中i叫虚数单位。注意:①复数通常用字母z表示，即复数a+bi（aR∈，bR)∈可记作:z=a+bi（aR,bR∈∈），把这一表示形式叫做复数的代数形式。②复数z=a+bi(aR∈，bR)∈把实数a，b叫做复数的实部和虚部。③全体复数所组成的集合叫复数集，记作C。问题：1是不是复数?若是，请指出实部与虚部即时训练，巩固新知即时训练，巩固新知3163.0i52i3ii235i+411、请指出下列复数的实部与虚部。、请指出下列复数的实部与虚部。0特别的，当特别的，当a=a=00且且b=b=00时，时，z=0z=0当当b=b=00时，时，zz为为实数实数当当bb≠0≠0时，时，zz为为虚数虚数当当a=a=00且且bb≠0≠0时，时，zz为为纯虚数纯虚数63.0i52对于复数z=a+bi（a∈R，b∈R）非纯虚数的虚数：a≠≠0,b≠≠0复数集虚数集实数集纯虚数集CR2、复数z=a+bi0)00)0)00)babbab实数(纯虚数(，虚数(非纯虚数(，复数的分类复数的分类3.复数集、虚数集、实数集、纯虚数集之间的关系.:,,,,,,|dbcadicbiaRdcbadicbiaRbabiaC且相等与我们规定中任取两个数在复数集4、相等的复数注意：一般复数只说相等或不等，而不能比大小，除非是实数。例1：判断下列说法是否正确0)1(2zCz时，当是纯虚数。则若iaRa)1(,)2(ibiaba则）若（,311,,)4(yxiyixCyx的充要条件是则若?3?2?111,:2纯虚数虚数实数是复数取什么值时实数例immzm;,1,011是实数复数时即当解zmm;,1,012是虚数复数时即当zmm.,1,01,013是纯虚数复数时即且当zmmm例例33已知已知，其中，其中iyyix)3()12(Ryx,求求xx与与y?y?是一定有实根的充要条件，方程已知04)3(2kxikxRk例例44K=-4在几何上，我们用什么来表示实数?想一想？实数的几何意义实数的几何意义类比实数的表示，可以用什么来表示复数？实数可以用数轴上的点来表示。实数数轴上的点(形)(数)一一对应复数z=a+bi有序实数对(a,b)直角坐标系中的点Z(a,b)xyobaZ(a,b)建立了平面直角坐标系来表示复数的平面x轴------实轴y轴------虚轴（数）（形）------复数平面(简称复平面)一一对应z=a+bi二、复数的几何意义（一）二、复数的几何意义（一）４３６５O２１思考1：复数与点的对应XY（１）２+５i；（２）－３+２i；（３）２－４i；（４）－３－５i；（５）５；（６）－３i；(A)在复平面内，对应于实数的点都在实轴上；(B)在复平面内，对应于纯虚数的点都在虚轴上；(C)在复平面内，实轴上的点所对应的复数都是实数；(D)在复平面内，虚轴上的点所对应的复数都是纯虚数。例1.辨析：1．下列命题中的假命题是（）D2．“a=0”是“复数a+bi(a,b∈R)是纯虚数”的（）。(A)必要不充分条件(B)充分不必要条件(C)充要条件(D)不充分不必要条件C3．“a=0”是“复数a+bi(a,b∈R)所对应的点在虚轴上”的（）。(A)必要不充分条件(B)充分不必要条件(C)充要条件(D)不充分不必要条件A例2已知复数z=(m2+m-6)+(m2+m-2)i在复平面内所对应的点位于第二象限，求实数m允许的取值范围。表示复数的点所在象限的问题复数的实部与虚部所满足的不...