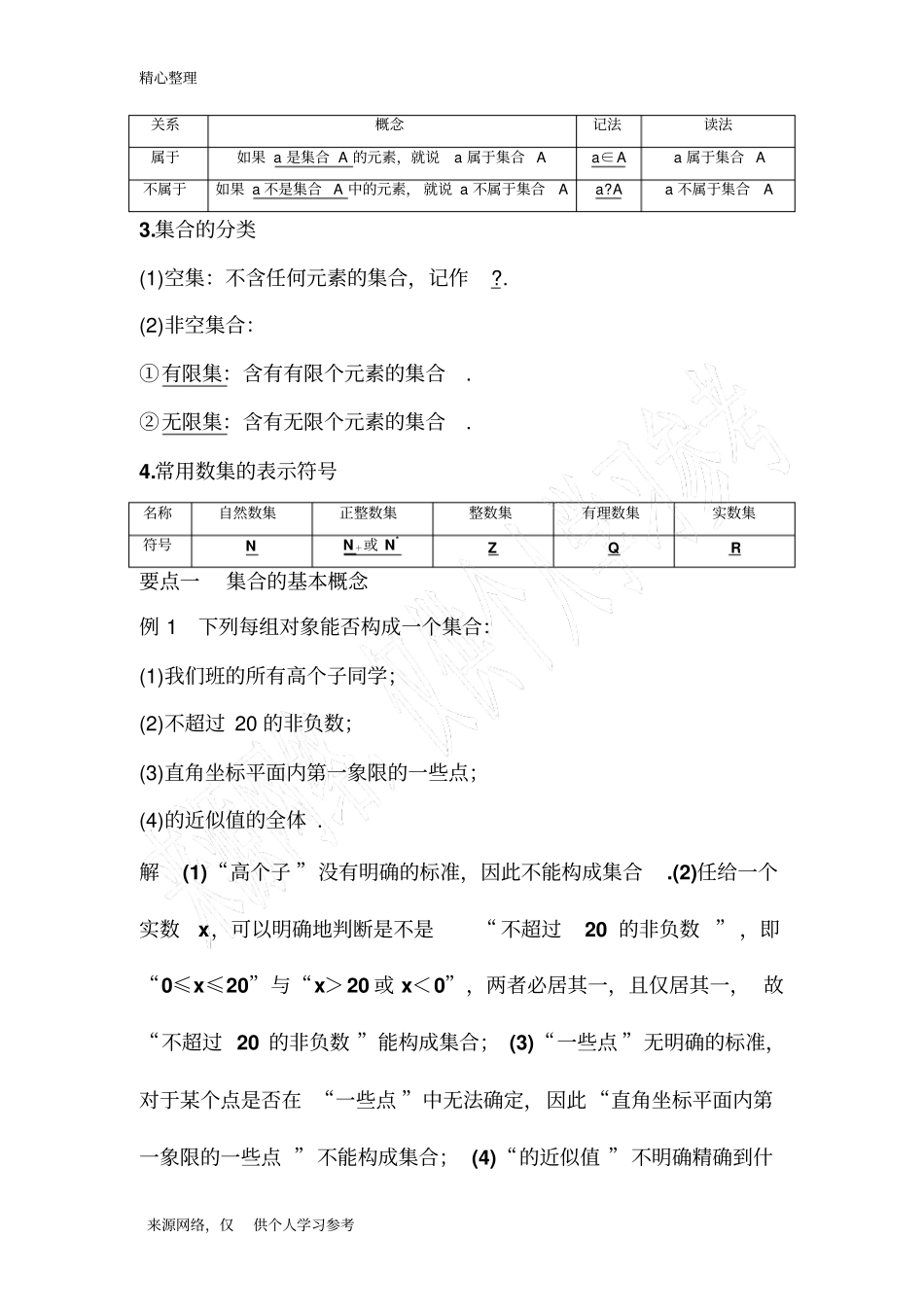
精心整理来源网络,仅供个人学习参考1.1集合与集合的表示方法1.1.1集合的概念[学习目标]1.了解集合的含义,体会元素与集合的关系.2.掌握集合中元素的两个特性.3.记住常用数集的表示符号并会应用.[知识链接]1.在初中,我们学习数的分类时,学过自然数的集合,正数的集合,负数的集合,有理数的集合.2.在初中几何里学习圆时,说圆是到定点的距离等于定长的点的集合.几何图形都可以看成点的集合.3.解不等式2x-1>3得x>2,即所有大于2的实数合在一起称为这个不等式的解集.4.一元二次方程x2-3x+2=0的解是x=1,x=2.[预习导引]1.元素与集合的概念(1)集合:把一些能够确定的不同的对象看成一个整体,就说这个整体是由这些对象的全体构成的集合(或集).(2)元素:构成集合的每个对象叫做这个集合的元素.(3)集合元素的特性:确定性、互异性.2.元素与集合的关系精心整理来源网络,仅供个人学习参考关系概念记法读法属于如果a是集合A的元素,就说a属于集合Aa∈Aa属于集合A不属于如果a不是集合A中的元素,就说a不属于集合Aa?Aa不属于集合A3.集合的分类(1)空集:不含任何元素的集合,记作?.(2)非空集合:①有限集:含有有限个元素的集合.②无限集:含有无限个元素的集合.4.常用数集的表示符号名称自然数集正整数集整数集有理数集实数集符号NN+或N*ZQR要点一集合的基本概念例1下列每组对象能否构成一个集合:(1)我们班的所有高个子同学;(2)不超过20的非负数;(3)直角坐标平面内第一象限的一些点;(4)的近似值的全体.解(1)“高个子”没有明确的标准,因此不能构成集合.(2)任给一个实数x,可以明确地判断是不是“不超过20的非负数”,即“0≤x≤20”与“x>20或x<0”,两者必居其一,且仅居其一,故“不超过20的非负数”能构成集合;(3)“一些点”无明确的标准,对于某个点是否在“一些点”中无法确定,因此“直角坐标平面内第一象限的一些点”不能构成集合;(4)“的近似值”不明确精确到什精心整理来源网络,仅供个人学习参考么程度,因此很难判断一个数如“2”是不是它的近似值,所以“的近似值”不能构成集合.规律方法判断一组对象能否构成集合的关键在于看是否有明确的判断标准,使给定的对象是“确定无疑”的还是“模棱两可”的.如果是“确定无疑”的,就可以构成集合;如果是“模棱两可”的,就不能构成集合.跟踪演练1下列所给的对象能构成集合的是________.(1)所有正三角形;(2)必修1课本上的所有难题;(3)比较接近1的正整数全体;(4)某校高一年级的16岁以下的学生.答案(1)(4)解析序号能否构成集合理由(1)能其中的元素是“三条边相等的三角形”(2)不能“难题”的标准是模糊的、不确定的,所以所给对象不确定,故不能构成集合(3)不能“比较接近1”的标准不明确,所以所给对象不确定,故不能构成集合(4)能其中的元素是“16岁以下的学生”要点二元素与集合的关系例2所给下列关系正确的个数是()①-∈R;②?Q;③0∈N*;④|-3|?N*.A.1B.2C.3D.4答案B解析-是实数,是无理数,∴①②正确.N*表示正整数集,∴③和④不正确.规律方法1.由集合中元素的确定性可知,对任意的元素a与集合A,精心整理来源网络,仅供个人学习参考在“a∈A”与“a?A”这两种情况中必有一种且只有一种成立.2.符号“∈”和“?”只表示元素与集合之间的关系,而不能用于表示其他关系.3.“∈”和“?”具有方向性,左边是元素,右边是集合.跟踪演练2设不等式3-2x<0的解集为M,下列关系中正确的是()A.0∈M,2∈MB.0?M,2∈MC.0∈M,2?MD.0?M,2?M答案B解析本题是判断0和2与集合M间的关系,因此只需判断0和2是否是不等式3-2x<0的解即可,当x=0时,3-2x=3>0,所以0?M;当x=2时,3-2x=-1<0,所以2∈M.要点三集合中元素的特性及应用例3已知集合B含有两个元素a-3和2a-1,若-3∈B,试求实数a的值.解 -3∈B,∴-3=a-3或-3=2a-1.若-3=a-3,则a=0.此时集合B含有两个元素-3,-1,符合题意;若-3=2a-1,则a=-1.此时集合B含有两个元素-4,-3,符合题意.综上所述,满足题意的实数a的值为0或-1.精心整理来源网络,仅供个人学习参考规律方法1.由于集合B含有两个元素,-3∈B,本题以-3是否等于a-3为...