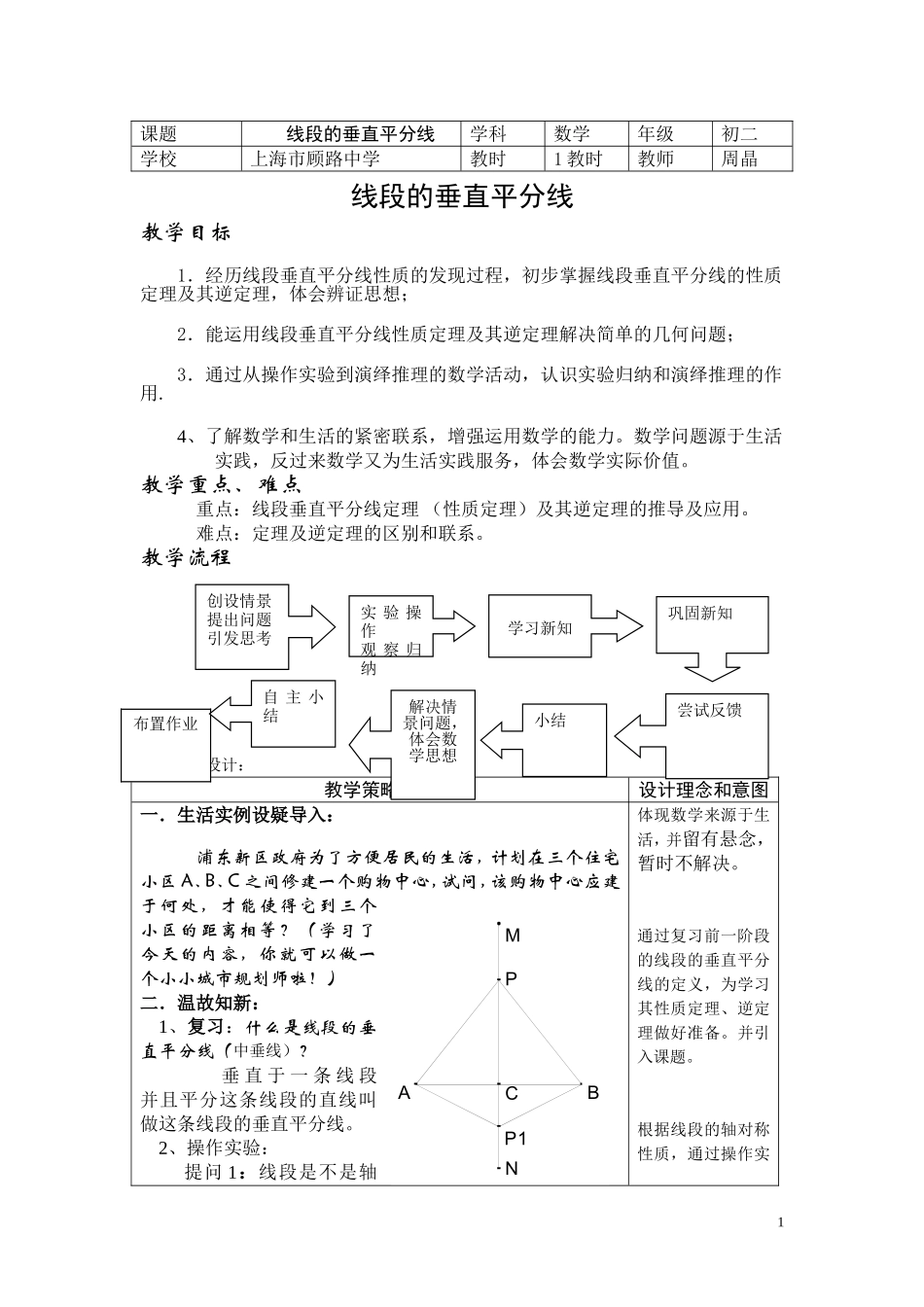
课题线段的垂直平分线学科数学年级初二学校上海市顾路中学教时1教时教师周晶线段的垂直平分线教学目标1.经历线段垂直平分线性质的发现过程,初步掌握线段垂直平分线的性质定理及其逆定理,体会辨证思想;2.能运用线段垂直平分线性质定理及其逆定理解决简单的几何问题;3.通过从操作实验到演绎推理的数学活动,认识实验归纳和演绎推理的作用.4、了解数学和生活的紧密联系,增强运用数学的能力。数学问题源于生活实践,反过来数学又为生活实践服务,体会数学实际价值。教学重点、难点重点:线段垂直平分线定理(性质定理)及其逆定理的推导及应用。难点:定理及逆定理的区别和联系。教学流程教学过程设计:教学策略方案设计理念和意图一.生活实例设疑导入:浦东新区政府为了方便居民的生活,计划在三个住宅小区A、B、C之间修建一个购物中心,试问,该购物中心应建于何处,才能使得它到三个小区的距离相等?(学习了今天的内容,你就可以做一个小小城市规划师啦!)二.温故知新:1、复习:什么是线段的垂直平分线(中垂线)?垂直于一条线段并且平分这条线段的直线叫做这条线段的垂直平分线。2、操作实验:提问1:线段是不是轴体现数学来源于生活,并留有悬念,暂时不解决。通过复习前一阶段的线段的垂直平分线的定义,为学习其性质定理、逆定理做好准备。并引入课题。根据线段的轴对称性质,通过操作实1CABMNPP1布置作业创设情景提出问题引发思考学习新知实验操作观察归纳巩固新知尝试反馈小结解决情景问题,体会数学思想自主小结对称图形?如果是,那么请说明它的对称轴在哪里?提问2:如图,线段AB关于直线MN对称,在直线MN上任取一点P,分别联结PA、PB,那么线段PA与PB一定相等吗?再取一点P1,P1A与PIB呢?操作:以直线MN为折痕将这个图形翻折,观察点P的位置动不动?点A与点B是否重合?你得到哪些线段相等?归纳可由学生归纳得出命题:线段垂直平分线上的任意一点和这条线段两个端点的距离相等。这个命题,是我们通过作图、观察、猜想得到的,还得在理论上加以证明是真命题才能作为定理。我们来证明这个命题的正确性:已知:如上图,直线MN是线段AB的垂直平分线,垂足为点C,点P在直线MN上.求证:PA=PB.(由学生分析思路后口述过程,教师板书)。性质定理:线段垂直平分线上的任意一点和这条线段两个端点的距离相等。符号语言: 点P在线段AB的垂直平分线MN上(已知)∴PA=PB(线段垂直平分线上的任意一点和这条线段两个端点的距离相等。)体问3:这条定理会有何作用呢?由该定理的结论可见,线段垂直平分线定理是证明两线段相等的一个依据。以后证明两条线段相等,我们又多了一个好办法-------线段的垂直平分线定理,且比用三角形全等更简便。提问4:任何定理都有逆命题。那么线段垂直平分线的性质定理的逆命题是什么?分析性质定理:如果一个点在一条线段的垂直平分线上,那么这个点到线段两个端点的距离相等。逆命题:如果一个点到一条线段两个端点的距离相等,那么这个点在这条线段的垂直平分线上。提问5:这个命题正确吗?已知:如图,QA=QB,求证:点Q在线段AB的垂直平分线上.分析:为了证明点Q在线段AB的垂直平分线上,可以先经过点Q作线段AB的垂线MN,然后证明直线MN平分线段AB.证明(略).启发学生叙述成为定理验归纳得到“线段垂直平分线上的点到这条线段两个端点的距离相等”的结论。用FLASH动画演示翻折过程是为了更直观的验证学生的猜想,让学生获得感性认识,为下面证明提供思考基础。将命题这一文字语言结合图形语言改写成“已知,求证”证明形式。通过提问,让学生思考定理的作用以及体悟使用该定理的简捷性。在获得定理的基础上,引导学生研究这个定理的逆命题。让学生增强运用这一方法主动获取知识的意识。先让学生写出逆命题,再根据已有的操作经验提出逆命题为真命题的猜想,然后进行证明。2QMNCBA逆定理:和一条线段两个端点距离相等的点,在这条线段的垂直平分线上。符号语言: PA=PB(已知)∴点P在线段AB的垂直平分线上(和一条线段两个端点距离相等的点,在这条线段的垂直平分线上。)可见,逆定理是证明点在直线上的依据.对比剖析定理和逆定理...