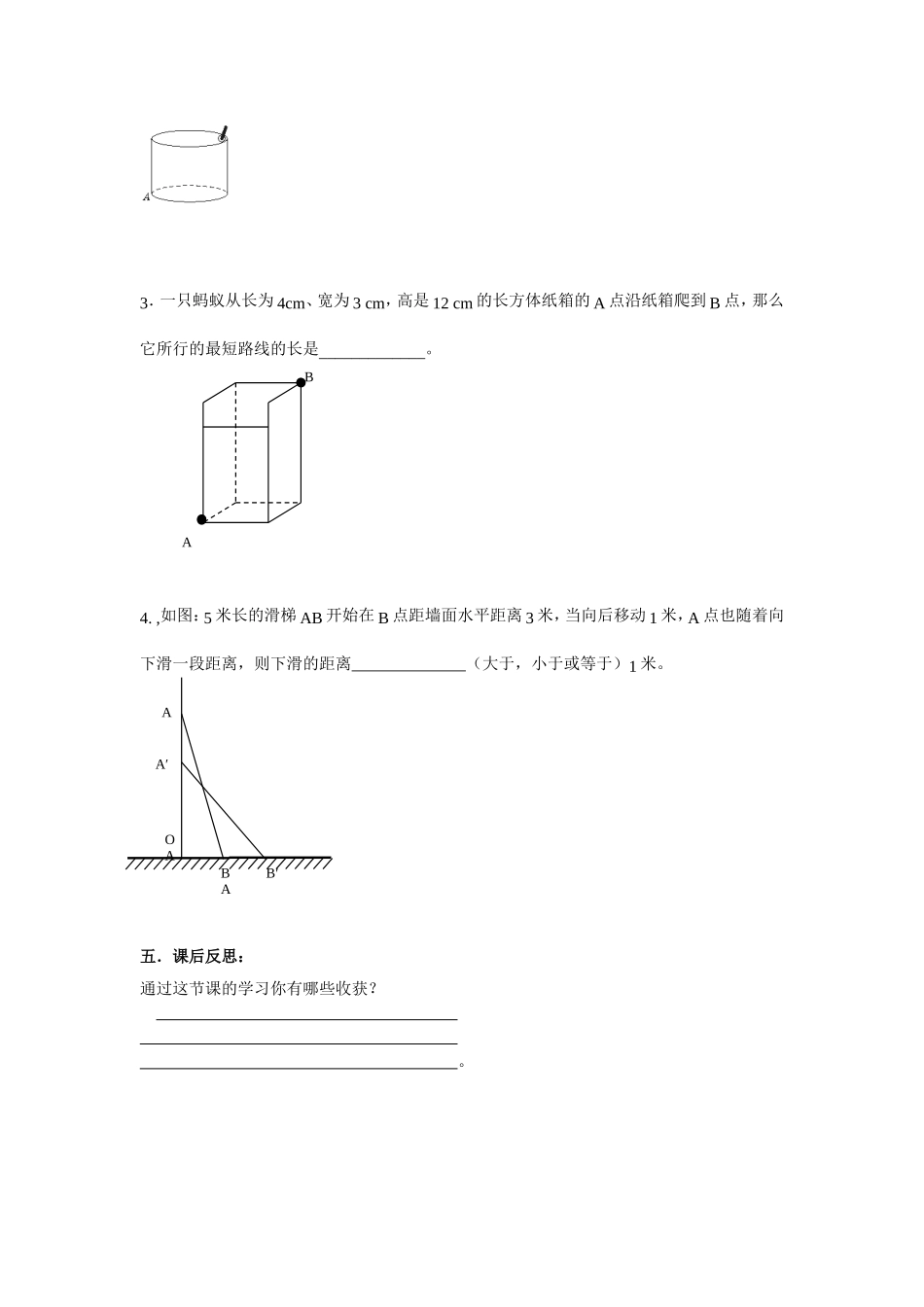
班级姓名日期1.3蚂蚁怎样走最近教学目标:能运用勾股定理及勾股定理的逆定理解决简单的实际问题.重、难点:利用数学中的建模思想构造直角三角形,利用勾股定理及逆定理,解决实际问题.一、温故:1.在Rt△ABC中,∠C=90°,则三边a,b,c的关系是______________。2.△ABC的三边a,b,c满足a2+b2=c2则三角形的形状是;二、导学:阅读教材P22完成下列问题:1.两点之间,最短;课本P22图中点A和点B能不能直接连线段;蚂蚁从点A到点B的线路可能经过哪些面;这些线路是直线还是曲线;当圆柱侧面展开成平面以后侧面上的蚂蚁线路是直线还是曲线;2.圆柱的底面圆周是直线还是曲线;当圆柱侧面展开成平面以后底面圆是直线还是曲线;它的长度是;怎样展开圆柱的侧面使AB在直角三角形中?(口述);由此可见,曲线段的长度应尽量转化成直线段进行计算。3.阅读教材P23,其中卷尺用来测量;书上的办法主要用的理论根据是;三、课堂练习:1.课本P23.随堂练习;2.如图,有一个高1.5米,半径是1米的圆柱形油桶,在靠近边的地方有一小孔,从孔中插入一铁棒,已知铁棒在油桶外的部分是0.5米,问这根铁棒应有多长?3.一只蚂蚁从长为4cm、宽为3cm,高是12cm的长方体纸箱的A点沿纸箱爬到B点,那么它所行的最短路线的长是_____________。4.,如图:5米长的滑梯AB开始在B点距墙面水平距离3米,当向后移动1米,A点也随着向下滑一段距离,则下滑的距离(大于,小于或等于)1米。五.课后反思:通过这节课的学习你有哪些收获?。ABAA′BAB′OA