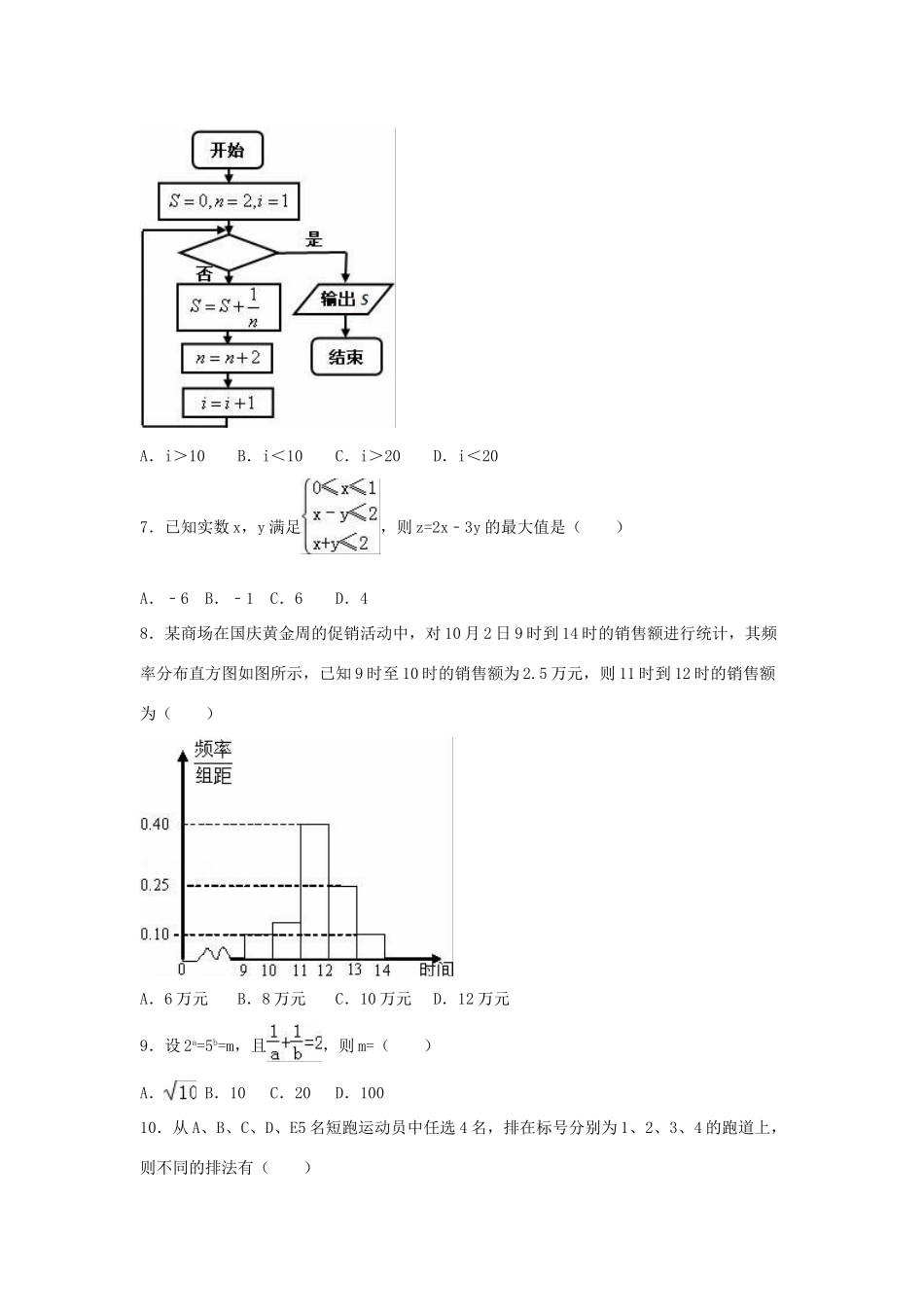
2015年陕西省铜川市高考数学三模试卷(理科)一、选择题(共12小题,每小题5分,满分60分.在每小题给出的四个选项中,选出符合题目要求的一项)1.设集合M={x|﹣1<x<1},N={x|x2≤x},则M∩N=()A.[0,1)B.(﹣1,1]C.[﹣1,1)D.(﹣1,0]2.若a+bi=(1+i)(2﹣i)(i是虚数单位,a,b是实数),则a+b的值是()A.1B.2C.3D.43.已知数列{an}为等差数列,且a1+a7+a13=π,则tan(a2+a12)的值为()A.B.C.D.4.某几何体的三视图如图所示,则该几何体的表面积为()A.24B.20+4C.28D.24+45.设a∈R,则“a=1”是“直线l1:ax+2y=0与直线l2:x+(a+1)y+4=0平行”的()A.充分不必要条件B.必要不充分条件C.充分必要条件D.既不充分又不必要条件6.给出计算的值的一个程序框图如图,其中判断框内应填入的条件是()A.i>10B.i<10C.i>20D.i<207.已知实数x,y满足,则z=2x﹣3y的最大值是()A.﹣6B.﹣1C.6D.48.某商场在国庆黄金周的促销活动中,对10月2日9时到14时的销售额进行统计,其频率分布直方图如图所示,已知9时至10时的销售额为2.5万元,则11时到12时的销售额为()A.6万元B.8万元C.10万元D.12万元9.设2a=5b=m,且,则m=()A.B.10C.20D.10010.从A、B、C、D、E5名短跑运动员中任选4名,排在标号分别为1、2、3、4的跑道上,则不同的排法有()A.24种B.48种C.120种D.124种11.设a<b,函数y=(a﹣x)(x﹣b)2的图象可能是()A.B.C.D.12.与椭圆共焦点且过点P(2,1)的双曲线方程是()A.B.C.D.二、本卷包括必考题和选考题两部分,第13题-第21题为必考题,每个考生必须作答,第22题-24题为选考题,考生根据要求作答填空题(共4小题,每小题5分,满分20分)13.若tanα=,则tan(α+)=.14.已知向量=(1,2),=(x,4),若||=2||,则x的值为.15.直线y=e2,y轴以及曲线y=ex围成的图形的面积为.16.某商人将彩电先按原价提高40%,然后“八折优惠”,结果是每台彩电比原价多赚144元,那么每台彩电原价是元.三、解答题(共5小题,满分60分.解答时应写出文字说明,证明过程或演算步骤)17.在△ABC中,内角A,B,C所对边长分别为a,b,c,,∠BAC=θ,a=4.(1)求b•c的最大值及θ的取值范围;(2)求函数的最大值和最小值.18.如图,AE⊥平面ABC,AE∥BD,AB=BC=CA=BD=2AE=2,F为CD中点.(Ⅰ)求证:EF⊥平面BCD;(Ⅱ)求二面角C﹣DE﹣A的大小;(Ⅲ)求点A到平面CDE的距离.19.某网站用“10分制”调查一社区人们的幸福度.现从调查人群中随机抽取16名,如图所示茎叶图记录了他们的幸福度分数(以小数点前的一位数字为茎,小数点后的一位数字为叶):(1)指出这组数据的众数和中位数;(2)若幸福度不低于9.5分,则称该人的幸福度为“极幸福”.求从这16人中随机选取3人,至多有1人是“极幸福”的概率;(3)以这16人的样本数据来估计整个社区的总体数据,若从该社区(人数很多)任选3人,记ξ表示抽到“极幸福”的人数,求ξ的分布列及数学期望.20.在平面直角坐标系xOy中,已知点A(﹣1,0),B(1,0),动点C满足条件:△ABC的周长为,记动点C的轨迹为曲线W.(1)求W的方程;(2)曲线W上是否存在这样的点P:它到直线x=﹣1的距离恰好等于它到点B的距离?若存在,求出点P的坐标;若不存在,请说明理由.21.已知函数f(x)=lnx,g(x)=x2﹣2x.(1)设h(x)=f(x+1)﹣g′(x)(其中g′(x)是g(x)的导函数),求h(x)的最大值;(2)证明:当0<b<a时,求证:f(a+b)﹣f(2a)<;(3)设k∈Z,当x>1时,不等式k(x﹣1)<xf(x)+3g′(x)+4恒成立,求k的最大值.选考题。在22题,23题,24题三题中任选一题作答,如果多做,则按所做的第一题记分选修4-1:几何证明选讲22.如图,圆O的直径AB=10,弦DE⊥AB于点H,BH=2.(Ⅰ)求DE的长;(Ⅱ)延长ED到P,过P作圆O的切线,切点为C,若PC=2,求PD的长.选修4-4:坐标系与参数方程23.已知直线l的极坐标方程为,圆C的参数方程为.(1)化直线l的方程为直角坐标方程;(2)化圆的方程为普通方程;(3)求直线l被圆截得的弦长.选修4-5:不等式...