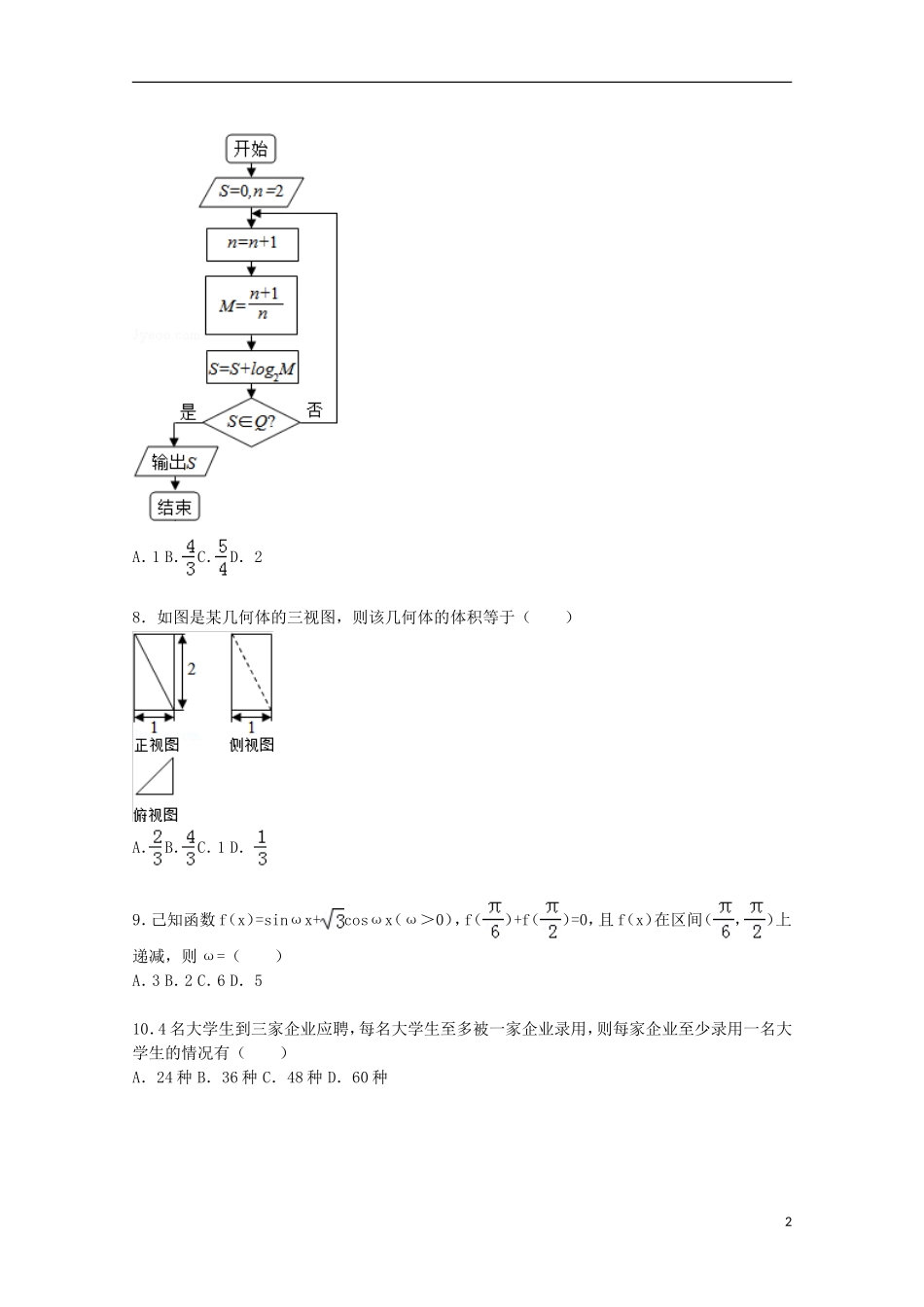
2014-2015学年河北省唐山市高三(上)期末数学试卷(理科)一、选择题:本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,有且只有一项符合题目要求.1.函数y=+的定义域为()A.[0,3]B.[1,3]C.[1,+∞)D.[3,+∞)2.某品牌空调在元旦期间举行促销活动,所示的茎叶图表示某专卖店记录的每天销售量情况(单位:台),则销售量的中位数是()A.13B.14C.15D.163.“k<9“是“方程+=1表示双曲线”的()A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件4.设变量x、y满足,则目标函数z=2x+3y的最小值为()A.7B.8C.22D.235.设Sn是等比数列{an}的前n项和,若=3,则=()A.2B.C.D.l或26.己知f(x)=的值域为R,那么a的取值范围是()A.(一∞,一1]B.(一l,)C.[﹣1,)D.(0,)7.执行如图所示的算法,则输出的结果是()1A.1B.C.D.28.如图是某几何体的三视图,则该几何体的体积等于()A.B.C.1D.9.己知函数f(x)=sinωx+cosωx(ω>0),f()+f()=0,且f(x)在区间(,)上递减,则ω=()A.3B.2C.6D.510.4名大学生到三家企业应聘,每名大学生至多被一家企业录用,则每家企业至少录用一名大学生的情况有()A.24种B.36种C.48种D.60种211.椭圆C:+=1(a>b>0)的左焦点为F,若F关于直线x+y=0的对称点A是椭圆C上的点,则椭圆C的离心率为()A.B.C.D.一l12.设函数f(x)=ax3﹣x+1(x∈R),若对于任意x∈[﹣1,1]都有f(x)≥0,则实数a的取值范围为()A.(﹣∞,2]B.[0+∞)C.[0,2]D.[1,2]二、填空题:本大题共4小题,每小题5分,共20分,把答案填写在题中横线上.13.若复数z满足z=i(2+z)(i为虚数单位),则z=.14.过点A(3,1)的直线l与圆C:x2+y2﹣4y﹣1=0相切于点B,则•=.15.在三棱锥P﹣ABC中,PB=6,AC=3,G为△PAC的重心,过点G作三棱锥的一个截面,使截面平行于直线PB和AC,则截面的周长为.16.数列{an}的前n项和为Sn,2Sn﹣nan=n(n∈N*),若S20=﹣360,则a2=.三、解答题:本大题共70分,其中(17)-(21)题为必考题,(22),(23),(24)题为选考题.解答应写出文字说明、证明过程或演算步骤.17.在△ABC中,角A,B,C所对的边分别为a,b,c,且csinB=bcosC=3.(I)求b;(Ⅱ)若△ABC的面积为,求c.18.如图,四棱锥P﹣ABCD的底面ABCD是平行四边形,PA⊥底面ABCD,∠PCD=90°,PA=AB=AC.(I)求证:AC⊥CD;(Ⅱ)点E在棱PC上,满足∠DAE=60°,求二面角B﹣AE﹣D的余弦值.19.某城市有东西南北四个进入城区主干道的入口,在早高峰时间段,时常发生交通拥堵现象,交警部门统计11月份30天内的拥堵天数.东西南北四个主干道入口的拥堵天数分别是18天,15天,9天,15天.假设每个入口发生拥堵现象互相独立,视频率为概率.(I)求该城市一天中早高峰时间段恰有三个入口发生拥堵的概率;3(Ⅱ)设翻乏示一天中早高峰时间段发生拥堵的主干道入口个数,求ξ的分布列及数学期望.20.已知抛物线y2=2px(p>0),过点C(一2,0)的直线l交抛物线于A,B两点,坐标原点为O,•=12.(I)求抛物线的方程;(Ⅱ)当以AB为直径的圆与y轴相切时,求直线l的方程.21.己知函数f(x)=aex+x2,g(x)=sin+bx,直线l与曲线y=f(x)切于点(0,f(0))且与曲线y=g(x)切于点(1,g(1)).(I)求a,b的值和直线l的方程.(Ⅱ)证明:f(x)>g(x)一、请考生在第(22),(23),(24)三题中任选一题作答,如果多做,则按所做的第一题记分.作答时【选修4-1:几何证明选讲】22.如图,四边形么BDC内接于圆,BD=CD,过C点的圆的切线与AB的延长线交于E点.(I)求证:∠EAC=2∠DCE;(Ⅱ)若BD⊥AB,BC=BE,AE=2,求AB的长.一、【选修4-4;坐标系与参数方程】23.极坐标系的极点为直角坐标系xOy的原点,极轴为x轴的正半轴,两种坐标系中的长度单位相同,已知曲线C的极坐标方程为ρ=2(cosθ+sinθ),斜率为的直线l交y轴于点E(0,1).(I)求C的直角坐标方程,l的参数方程;(Ⅱ)直线l与曲线C交于A、B两点,求|EA|+|EB|.一、【选修4-5:不等式选讲】24....