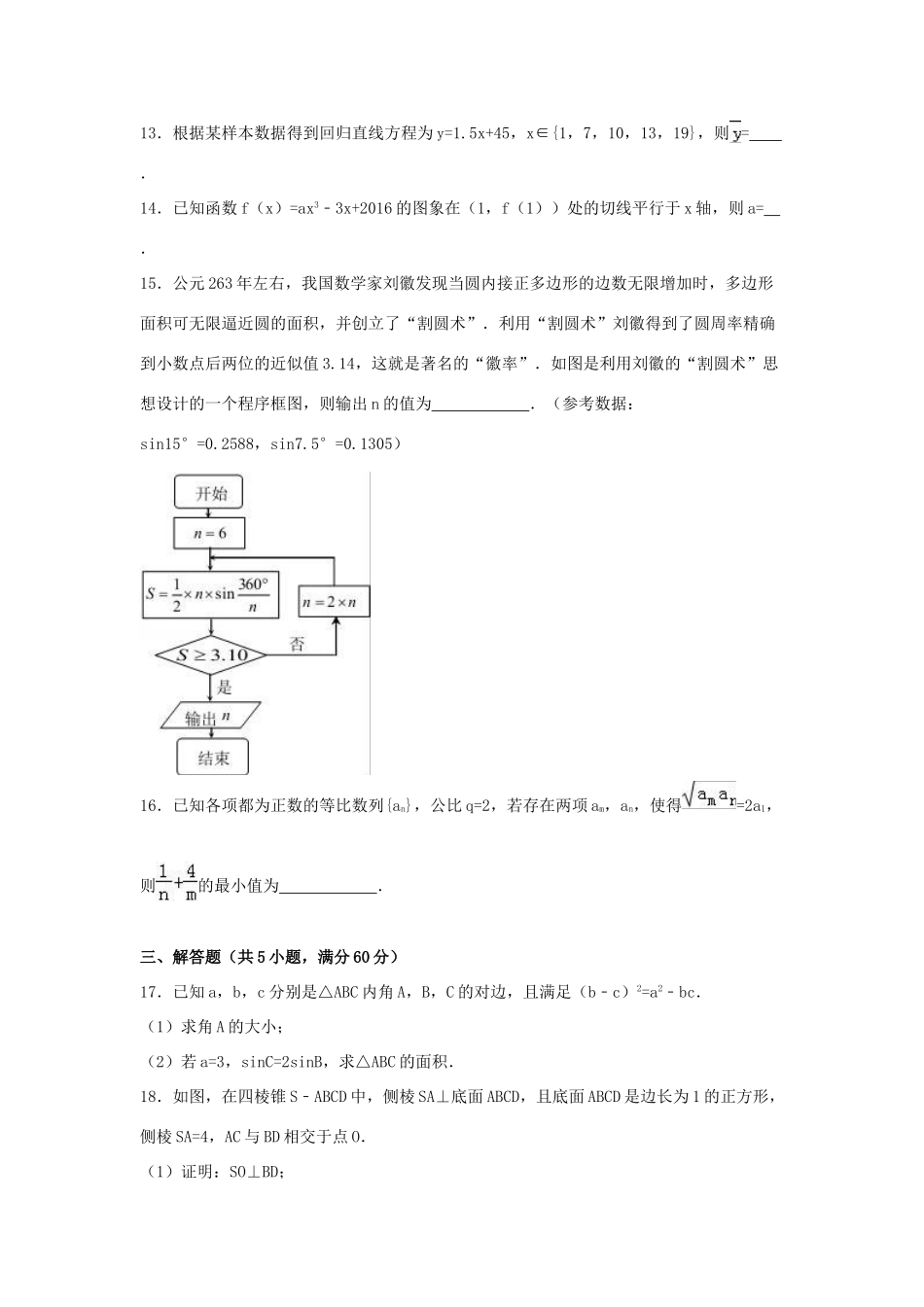
2016年陕西省高考数学全真模拟试卷(文科)(三)一、选择题(共12小题,每小题5分,满分60分)1.已知集合A={x|x≥0},B={﹣1,0,1},则A∩B=()A.{1}B.{0,1}C.{﹣1,0}D.∅2.已知向量,则向量=()A.(﹣1,1)B.(﹣1,0)C.(1,1)D.(0,﹣1)3.若复数z满足,其中i为复数单位,则z=()A.1﹣iB.1+iC.﹣1﹣iD.﹣1+i4.已知抛物线方程为,则该抛物线的焦点坐标为()A.(0,﹣1)B.C.D.(0,1)5.下列函数中,既是偶函数又在区间(0,+∞)上单调递减的是()A.y=lnxB.y=cosxC.y=﹣x2D.6.等差数列{an}的前n项和为Sn,若a2+a5+a8=15,则S9的值()A.54B.45C.36D.277.已知x、y满足约束条件,则z=x﹣y的最大值为()A.1B.﹣1C.2D.﹣28.函数f(x)=2sin(ωx+φ)(ω>0,﹣φ<)的部分图象如图所示,则f()=()A.B.1C.D.29.已知某个几何体的三视图如图所示,该几何体的体积是()A.4B.12C.8D.810.已知菱形ABCD的边长为4,,若在菱形内取一点,则该点到菱形的四个顶点的距离均大于1的概率为()A.B.C.D.11.双曲线的实轴长与虚轴长之和等于其焦距的倍,且一个顶点的坐标为(0,2),则双曲线的标准方程为()A.﹣=1B.﹣=1C.﹣=1D.﹣=112.定义f(x)•g(x)=,函数F(x)=(x2﹣1)•(x)﹣k的图象与x轴有两个不同的交点,则实数k的取值范围是()A.k≥3或0≤k<1B.k>3或0<k<1C.k≤1或k≥3D.0≤k≤1或k>3二、填空题(共4小题,每小题5分,满分20分)13.根据某样本数据得到回归直线方程为y=1.5x+45,x∈{1,7,10,13,19},则=.14.已知函数f(x)=ax3﹣3x+2016的图象在(1,f(1))处的切线平行于x轴,则a=.15.公元263年左右,我国数学家刘徽发现当圆内接正多边形的边数无限增加时,多边形面积可无限逼近圆的面积,并创立了“割圆术”.利用“割圆术”刘徽得到了圆周率精确到小数点后两位的近似值3.14,这就是著名的“徽率”.如图是利用刘徽的“割圆术”思想设计的一个程序框图,则输出n的值为.(参考数据:sin15°=0.2588,sin7.5°=0.1305)16.已知各项都为正数的等比数列{an},公比q=2,若存在两项am,an,使得=2a1,则的最小值为.三、解答题(共5小题,满分60分)17.已知a,b,c分别是△ABC内角A,B,C的对边,且满足(b﹣c)2=a2﹣bc.(1)求角A的大小;(2)若a=3,sinC=2sinB,求△ABC的面积.18.如图,在四棱锥S﹣ABCD中,侧棱SA⊥底面ABCD,且底面ABCD是边长为1的正方形,侧棱SA=4,AC与BD相交于点O.(1)证明:SO⊥BD;(2)求三棱锥O﹣SCD的体积.19.2015年1月1日新《环境保护法》实施后,2015年3月18日,交通运输部发布《关于加快推进新能源汽车在交通运输行业推广应用的实施意见》,意见指出,至2020年,新能源汽车在交通运输行业的应用初具规模,在城市公交、出租汽车和城市物流配送等领域的总量达到30万辆;新能源汽车配套服务设施基本完备,新能源汽车运营效率和安全水平明显提升.随着新能源汽车的迅速发展,关于新能源汽车是纯电动汽车的续航里程(单次充电后能行驶的最大里程)一直是消费者最为关注的话题.对于这一问题渭南市某高中研究性学习小组从汽车市场上随机抽取n辆纯电动汽车调查其续航里程,被调查汽车的续航里程全部介于50公里和300公里之间,将统计结果分成5组:[50,100),[100,150),[150,200),[200,250),[250,300],绘制如图所示的频率分布直方图.(1)若续航里程在[100,150)的车辆数为5,求抽取的样本容量n及频率分布直方图中x的值;(2)在(1)的条件下,若从续航里程在[200,300]的车辆中随机抽取2辆车,求其中恰有一辆车的续航里程为[250,300]的概率.20.在直角坐标系xOy中,已知中心在原点,离心率为e=的椭圆E的一个焦点为圆C:x2+y2﹣2x﹣1=0的圆心.(1)求椭圆E的方程;(2)是否存在斜率为﹣1的直线l,与椭圆交于A,B两点,且满足OA⊥OB.若存在,求该直线方程;若不存在,请说明理由.21.已知函数f(x)=x2﹣2x+alnx(a∈R).(Ⅰ)当a=2时,求函数f(x)在(1,f(1))处的切线方程;(Ⅱ)当a>0时,求函数f(x)的单调区...