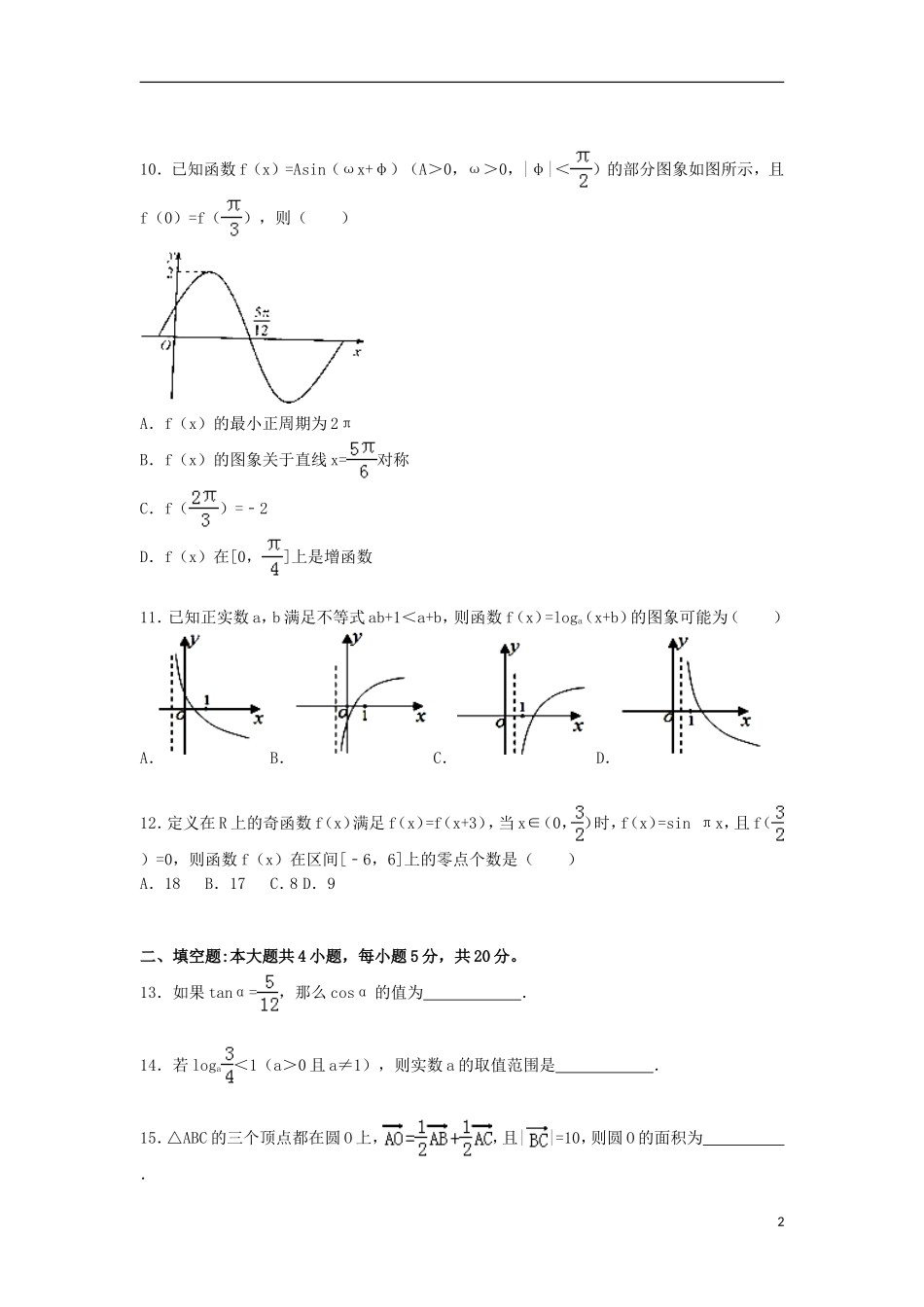
2015-2016学年河北省唐山市高一(上)期末数学试卷一、选择题:本大题共12小题,每小题5分,共60分。在每小题给出的四个选项中,有且只有一项符合题目要求。1.已知全集U={x∈N|x<6},集合A={1,3},B={3,5},则∁U(A∪B)=()A.{0,2,4}B.{2,4}C.{0,3,4}D.{3,4}2.sin660°=()A.﹣B.C.﹣D.3.下列函数中与函数y=x为同一函数的是()A.y=B.y=()2C.y=D.y=lg10x4.函数f(x)=﹣log3x的零点所在的一个区间是()A.(0,1)B.(1,2)C.(2,3)D.(3,4)5.已知向量=(1,2),=(1,0),=(3,4).若λ为实数,(+λ)∥,则λ=()A.B.C.1D.26.已知a=ln0.2,b=20.3,c=0.30.2,则实数a,b,c的大小关系为()A.a>b>cB.c>b>aC.b>c>aD.b>a>c7.如图,圆C中,弦AB的长度为4,则•=()A.12B.8C.4D.28.若cos()=﹣,则cos()=()A.B.﹣C.D.9.把函数y=sin(4x+φ)图象上各点的横坐标伸长到原来的2倍(纵坐标不变),再将图象上所有的点向右平个单位,所得图象关于y轴对称,则φ的一个可能值为()A.B.C.D.110.已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<)的部分图象如图所示,且f(0)=f(),则()A.f(x)的最小正周期为2πB.f(x)的图象关于直线x=对称C.f()=﹣2D.f(x)在[0,]上是增函数11.已知正实数a,b满足不等式ab+1<a+b,则函数f(x)=loga(x+b)的图象可能为()A.B.C.D.12.定义在R上的奇函数f(x)满足f(x)=f(x+3),当x∈(0,)时,f(x)=sinπx,且f()=0,则函数f(x)在区间[﹣6,6]上的零点个数是()A.18B.17C.8D.9二、填空题:本大题共4小题,每小题5分,共20分。13.如果tanα=,那么cosα的值为.14.若loga<1(a>0且a≠1),则实数a的取值范围是.15.△ABC的三个顶点都在圆O上,,且||=10,则圆O的面积为.216.已知ω>0,在函数y=sinωx与函数y=cosωx图象的交点中,距离最近的两个交点间的距离为,则ω=.三、解答题:本大题共6小题,共70分。解答应写出文字说明、证明过程或演算步骤。17.已知sinα=,cosβ=,α∈(,π),β∈(﹣,0)(Ⅰ)求cosα,tanβ;(Ⅱ)求tan(α+β)的值.18.已知函数f(x)=2(sin)•cos﹣1.(Ⅰ)求函数f(x)的最小正周期和单调递增区间;(Ⅱ)当x∈[﹣1,1]时,求函数f(x)的值域.19.在Rt△ABC中,∠BCA=90°,P为边AB上的一点,.(Ⅰ)若λ=3,试用,表示;(Ⅱ)若||=4,||=3,且•=﹣6,求λ的值.20.已知函数f(x)=且f[f()]=(Ⅰ)求实数p的值;(Ⅱ)若方程f(x)﹣m=0有3个不同的解,求实数m的取值范围;(Ⅲ)若x∈[﹣1,16]时,f(x)≤n+1恒成立,求实数n的取值范围.21.如图所示,长方形ABCD中,AB=2,BC=4,以D为圆心的两个圆心半圆,半径分别为1和2,G为大半圆直径的右端点,E为大半圆上的一个动点,DE与小半圆交于点F,EM⊥BC,垂足为M,EM与大半圆直径交于点H,FN⊥EM,垂足为N.(Ⅰ)设∠GDE=30°,求MN的长度;(Ⅱ)求△BMN的面积的最大值.322.已知定义域为R的函数f(x)=是奇函数.(Ⅰ)求实数a的值;(Ⅱ)判断函数f(x)在R上的单调性,并利用函数单调性的定义证明;(Ⅲ)若不等式f(2x+1)+f(k•2x+1+2k)>0在区间[0,+∞)上有解,求实数k的取值范围.42015-2016学年河北省唐山市高一(上)期末数学试卷参考答案与试题解析一、选择题:本大题共12小题,每小题5分,共60分。在每小题给出的四个选项中,有且只有一项符合题目要求。1.已知全集U={x∈N|x<6},集合A={1,3},B={3,5},则∁U(A∪B)=()A.{0,2,4}B.{2,4}C.{0,3,4}D.{3,4}【考点】交、并、补集的混合运算.【专题】计算题;集合思想;定义法;集合.【分析】列举出全集U中的元素,由A与B求出两集合的并集,找出并集的补集即可.【解答】解: 全集U={x∈N|x<6}={0,1,2,3,4,5},集合A={1,3},B={3,5},∴A∪B={1,3,5},则∁U(A∪B)={0,2,4},故选:A.【点评】此题考查了交、并、补集的混合运算,熟练掌握各自的定义是解本题的关键.2.sin660°=()A.﹣B.C.﹣D.【考...