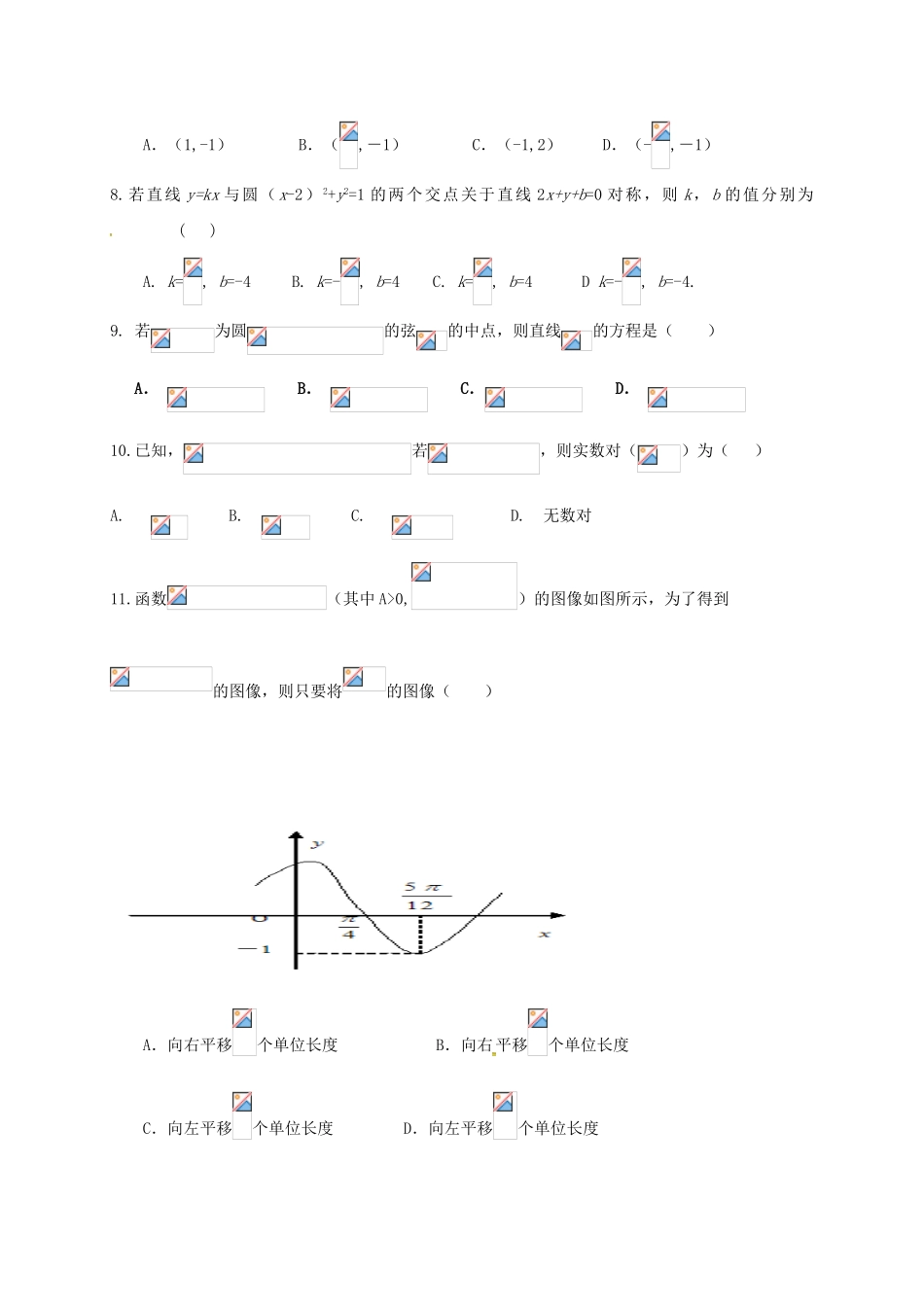
2016—2017第二学期五月月考试卷高一数学本试卷分第I卷(选择题)和第II卷(非选择题)两部分.共150分.考试时间120分钟.第I卷(选择题共60分)一、选择题(每小题5分,每小题只有一项是符合题目要求的)1.的值是()A.B.C.D.2.已知向量,,若,则实数的值为()A.B.C.-D.13.若,则的终边在()A.第一象限B.第四象限C.第二或第三象限D.第一或第四象限4.若为所在平面内的一点,满足,则点的位置为()A.在的内部B.在的外部C.在边所在的直线上D.在边所在的直线上5.是边长为的等边三角形,已知向量,满足,,则下列结论正确的是()A.B.C.D.6.已知且,其中,则关于的值,以下四个答案中,可能正确的是()A.-3B.3或C.D.或7.圆的方程是(x-1)(x+2)+(y-2)(y+4)=0,则圆心的坐标是()A.(1,-1)B.(,-1)C.(-1,2)D.(-,-1)8.若直线y=kx与圆(x-2)2+y2=1的两个交点关于直线2x+y+b=0对称,则k,b的值分别为()A.k=,b=-4B.k=-,b=4C.k=,b=4Dk=-,b=-4.9.若为圆的弦的中点,则直线的方程是()A.B.C.D.10.已知,若,则实数对()为()A.B.C.D.无数对11.函数(其中A>0,)的图像如图所示,为了得到的图像,则只要将的图像()A.向右平移个单位长度B.向右平移个单位长度C.向左平移个单位长度D.向左平移个单位长度12.已知函数,如果存在实数,使得对任意的实数,都有成立,则的最小正值为()A.B.C.D.二、填空题(本大题共4小题,每小题5分,共20分.)13.已知点A在x轴上,点B(1,2,0),且|AB|=,则点A的坐标是__________.14.函数的定义域是15.若非零向量满足,且,则与的夹角为________16.对于函数f(x)=,给出下列四个命题:①该函数是以π为最小正周期的周期函数;②当且仅当x=π+kπ(k∈Z)时,该函数取得最小值-1;③该函数的图象关于x=+2kπ(k∈Z)对称;④当且仅当2kπ0),则有a·b=λ+4λ=10,∴λ=2,∴a=(2,4).(2)∵b·c=1×2-2×1=0,a·b=1×2+2×4=10,∴a(b·c)=0a=0,(a·b)c=10×(2,-1)=(20,-10)18、解:(Ⅰ)∵,∴即共线,∴三点共线.(Ⅱ)∵,∴,,,解得.19、解:(1)由图象知的最小正周期故将点代入的解析式得,又,∴故函数的解析式为(2)由,得,所以减区间为:(3)当时,所以当,即时,的最大值20、解:Ⅰ)曲线与坐标轴的交点为(0,1)(3,故可设圆的圆心坐标为(3,t),则有+解得t=1,则圆的半径为.所以圆的方程为.(Ⅱ)设A(,B(其坐标满足方程组消去y得到方程由已知可得判别式=56-16a-4>0由韦达定理可得,①由可得又,所以2,②由①②可得a=-1,满足>0,故a=-1.21、解:(Ⅰ)∵·=cos(-)cos()+sin(+)sin()=sincos-sincos=0∴⊥.(Ⅱ)由⊥得·=0即[+(t2+3)]·(-k+t)=0∴-k+(t3+3t)+[t-k(t2+3)]·=0∴-k||2+(t3+3t)||2=0又∵||2=1,||2=1∴-k+t3+3t=0∴k=t3+3t∴==t2+t+3故当t=-时,取得最小值,为.22、解:∴(1)则有化简得:(2)又则化简有:联立解得或则四边形为对角线互相垂直的梯形当此时当此时