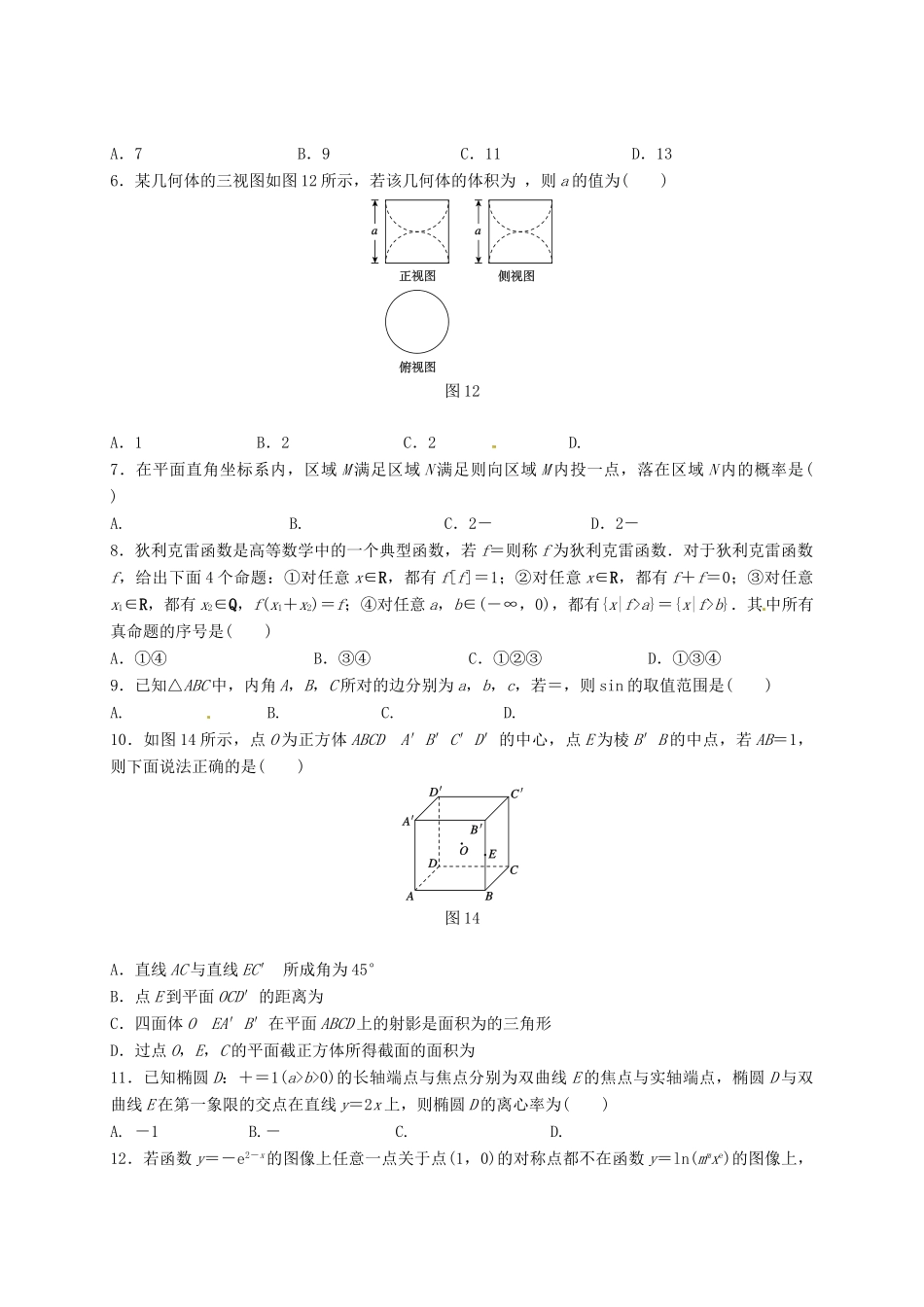
2017届高三普通班考前模拟考试(二)数学(理科)时间:120分钟满分:150分第Ⅰ卷(选择题共60分)一、选择题:本大题共12小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是符合题目要求的.1.已知集合M={y|y=x},N={x|x2+y2=1},则M∩N=()A.B.C.D.[-1,1]2.若定义运算=ad-bc,则满足=-2的复数z是()A.1-iB.1+iC.-1+iD.-1-i3.下列函数中,既是奇函数又零点个数最多的是()A.y=-x3-1,x∈RB.y=x+,x∈R,且x≠0C.y=-x3-x,x∈RD.y=-x3(x2-1),x∈R,且x≠0图314.如图31所示,三棱柱ABCA1B1C1的侧棱长和底边各边长均为2,且侧棱AA1⊥平面A1B1C1,正视图是边长为2的正方形,则该三棱柱的侧视图的面积为()A.B.2C.D.25.对一个做直线运动的质点的运动过程观测了8次,得到如下表所示的数据:观测次第i12345678观测数据ai4041434344464748在上述数据的统计分析中,一部分计算见如图32所示的程序框图(其中a是这8个观测数据的平均数),则输出S的值是()图32A.7B.9C.11D.136.某几何体的三视图如图12所示,若该几何体的体积为,则a的值为()图12A.1B.2C.2D.7.在平面直角坐标系内,区域M满足区域N满足则向区域M内投一点,落在区域N内的概率是()A.B.C.2-D.2-8.狄利克雷函数是高等数学中的一个典型函数,若f=则称f为狄利克雷函数.对于狄利克雷函数f,给出下面4个命题:①对任意x∈R,都有f[f]=1;②对任意x∈R,都有f+f=0;③对任意x1∈R,都有x2∈Q,f(x1+x2)=f;④对任意a,b∈(-∞,0),都有{x|f>a}={x|f>b}.其中所有真命题的序号是()A.①④B.③④C.①②③D.①③④9.已知△ABC中,内角A,B,C所对的边分别为a,b,c,若=,则sin的取值范围是()A.B.C.D.10.如图14所示,点O为正方体ABCDA′B′C′D′的中心,点E为棱B′B的中点,若AB=1,则下面说法正确的是()图14A.直线AC与直线EC′所成角为45°B.点E到平面OCD′的距离为C.四面体OEA′B′在平面ABCD上的射影是面积为的三角形D.过点O,E,C的平面截正方体所得截面的面积为11.已知椭圆D:+=1(a>b>0)的长轴端点与焦点分别为双曲线E的焦点与实轴端点,椭圆D与双曲线E在第一象限的交点在直线y=2x上,则椭圆D的离心率为()A.-1B.-C.D.12.若函数y=-e2-x的图像上任意一点关于点(1,0)的对称点都不在函数y=ln(mmxe)的图像上,则正整数m的取值集合为()A.B.C.D.第Ⅱ卷(非选择题共90分)本卷包括必考题和选考题两部分.第13题~第21题为必考题,每个试题考生都必须作答,第22题~第23题为选考题,考生根据要求作答.二、填空题:本大题共4小题,每小题5分,共20分.13.已知,则展开式中,项的系数为___________;14.已知函数为偶函数,则______________;15.正三角形ABC的边长为2,将它沿高AD翻折,使点B与点C间的距离为,此时四面体ABCD的外接球的表面积为16.数列的前项和为,且,用表示不超过的最大整数,如,设,则数列的前2n项和为_____.三、解答题:本大题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.17.(本小题满分12分)已知数列满足.(1)求;(2)是否存在实数,使数列为等差数列,若存在,求出请求出的值,若不存在,说明理由.18.(本小题满分12分)2017年两会继续关注了乡村教师的问题,随着城乡发展失衡,乡村教师待遇得不到保障,流失现象严重,教师短缺会严重影响乡村孩子的教育问题,为此,某市今年要为两所乡村中学招聘储备未来三年的教师,现在每招聘一名教师需要2万元,若三年后教师严重短缺时再招聘,由于各种因素,则每招聘一名教师需要5万元,已知现在该乡村中学无多余教师,为决策应招聘多少乡村教师搜集并整理了该市100所乡村中学在过去三年内的教师流失数,得到下面的柱状图:流失的教师数以这100所乡村中学流失教师数的频率代替1所乡村中学流失教师数发生的概率,记表示两所乡村中学在过去三年共流失的教师数,表示今年为两所乡村中学招聘的教师数.为保障乡村孩子教育部受影响,若未来三年内教师有短缺,则第四年马上招聘.(Ⅰ)求的分布列;(Ⅱ)若要求,确定的最小值;(Ⅲ)以未来四年内招聘教师所需费用的...