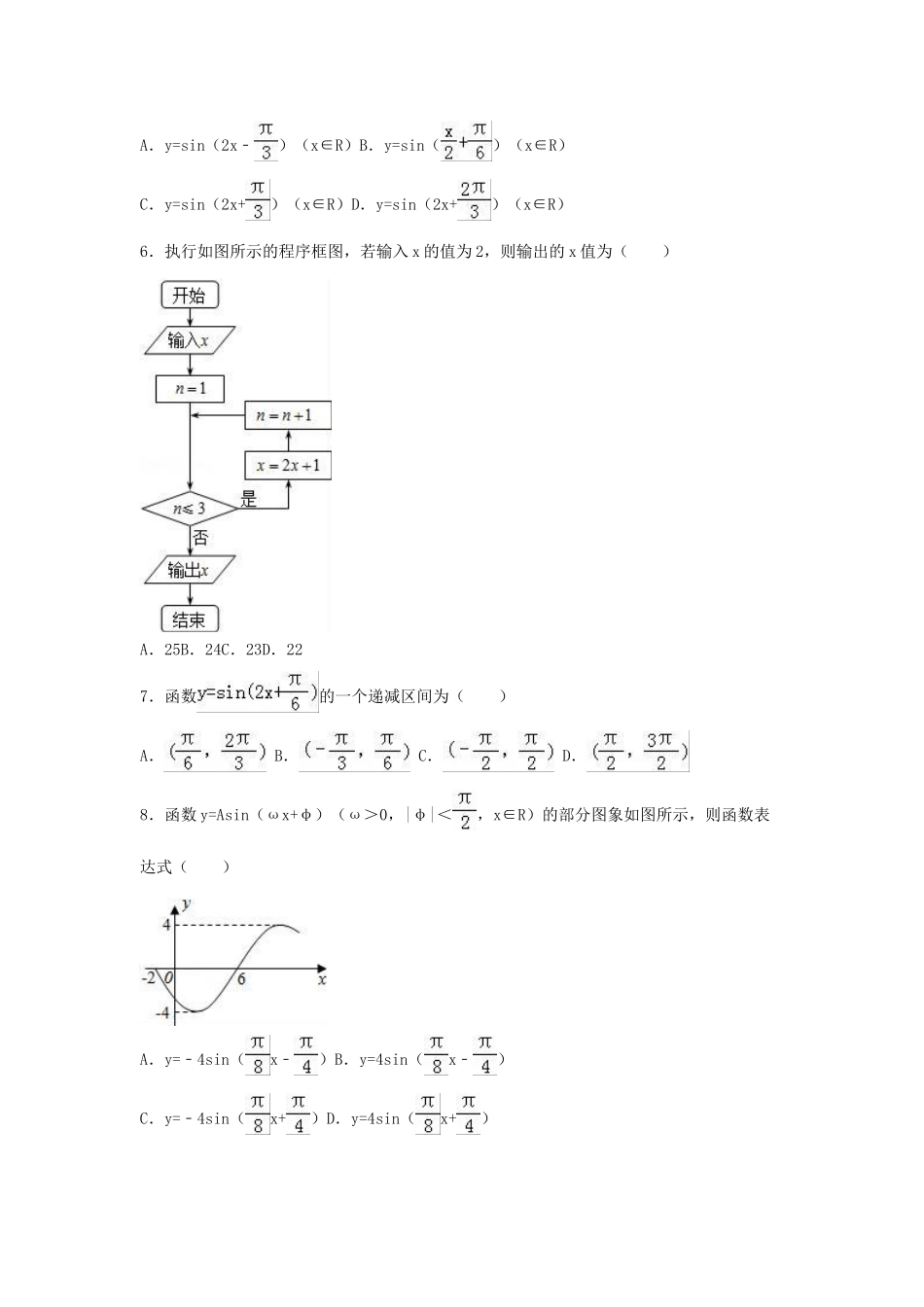
2015-2016学年河南省郑州市高一(下)期末数学试卷一、选择题本大题共12小题,每小题5分,共60分。在每小题给出的四个选项中,只有一项是符合题目要求的1.sin780°等于()A.﹣B.C.D.﹣2.某商场想通过检查发票存根及销售记录的2%来快速估计每月的销售总额,采取如下方法:从某本发票的存根中随机抽一张,如15号,然后按序往后将65号,115号,165号,…发票存根上的销售额组成一个调查样本.这种抽取样本的方法是()A.抽签法B.随机数法C.系统抽样法D.其他方式的抽样3.已知扇形的半径为2,面积为4,则这个扇形圆心角的弧度数为()A.B.2C.2D.24.从甲乙两个城市分别随机抽取16台自动售货机,对其销售额进行统计,统计数据用茎叶图表示(如图所示),设甲乙两组数据的平均数分别为,,中位数分别为m甲,m乙,则()A.,m甲>m乙B.,m甲<m乙C.,m甲>m乙D.,m甲<m乙5.把函数y=sinx(x∈R)图象上所有点的横坐标缩短到原来的倍(纵坐标不变),再把图象上所有的点向左平行移动个单位长度,得到的图象所表示的函数是()A.y=sin(2x﹣)(x∈R)B.y=sin()(x∈R)C.y=sin(2x+)(x∈R)D.y=sin(2x+)(x∈R)6.执行如图所示的程序框图,若输入x的值为2,则输出的x值为()A.25B.24C.23D.227.函数的一个递减区间为()A.B.C.D.8.函数y=Asin(ωx+φ)(ω>0,|φ|<,x∈R)的部分图象如图所示,则函数表达式()A.y=﹣4sin(x﹣)B.y=4sin(x﹣)C.y=﹣4sin(x+)D.y=4sin(x+)9.已知tan(α+β)=,tan(β﹣)=,那么tan(α+)等于()A.B.C.D.10.在直角△ABC中,∠BCA=90°,CA=CB=1,P为AB边上的点且=λ,若•≥•,则λ的取值范围是()A.[,1]B.[,1]C.[,]D.[,]11.已知A为△ABC的最小内角,若向量=(cos2A,sin2A),=(,),则的取值范围是()A.(﹣∞,)B.(﹣1,)C.[﹣,)D.[﹣,+∞)12.已知P、M、N是单位圆上互不相同的三个点,且满足||=||,则•的最小值是()A.﹣B.﹣C.﹣D.﹣1二、填空题(本大题共2小题,每小题5分,共20分,将答案填在答题卡上的相应位置)13.已知,均为单位向量,<,>=60°,那么|+3|=.14.如图所示,四个相同的直角三角形与中间的小正方形拼成的一个边长为2的大正方形,若直角三角形中较小的锐角,现在向该正方形区域内随机地投掷一枚飞镖,飞镖落在小正方形内概率是.15.求函数f(x)=sinx+cosx+sinxcosx的值域.16.f(x)=3sin(﹣x+),若实数m满足f()>f(),则m的取值范围是.三、解答题:本大题共6小题,共70分。解答应写出文字说明,证明过程或演算步骤17.已知:、、是同一平面内的三个向量,其中=(1,2)(1)若||=2,且∥,求的坐标;(2)若||=,且+2与2﹣垂直,求与的夹角θ.18.某个体服装店经营某种服装,在某周内获纯利y(元)与该周每天销售这种服装件数x之间的一组数据关系如下表x3456789y66697381899091(1)求纯利y与每天销售件数x之间的回归方程;(2)若该周内某天销售服装20件,估计可获纯利多少元?已知:x=280,y=45309,xiyi=3487,=,=﹣.19.某高校在2012年的自主招生考试成绩中随机抽取100名学生的笔试成绩,按成绩分组:第1组[75,80),第2组[80,85),第3组[85,90),第4组[90,95),第5组[95,100]得到的频率分布直方图如图所示.(Ⅰ)分别求第3,4,5组的频率;(Ⅱ)若该校决定在笔试成绩高的第3,4,5组中用分层抽样抽取6名学生进入第二轮面试,求第3,4,5组每组各抽取多少名学生进入第二轮面试?(Ⅲ)在(Ⅱ)的前提下,学校决定在这6名学生中随机抽取2名学生接受甲考官的面试,求第4组至少有一名学生被甲考官面试的概率.20.如图,一个水轮的半径为4m,水轮圆心O距离水面2m,已知水轮每分钟转动5圈,如果当水轮上点P从水中浮现时(图中点p0)开始计算时间.(1)将点p距离水面的高度z(m)表示为时间t(s)的函数;(2)点p第一次到达最高点大约需要多少时间?21.已知关于x的方程2x2﹣bx+=0的两根为sinθ、cosθ,θ∈(,).(1)求实数b的值;(2)求+的值.22.已知x0,x0+是函数f(x)=cos2(wx﹣)﹣sin...