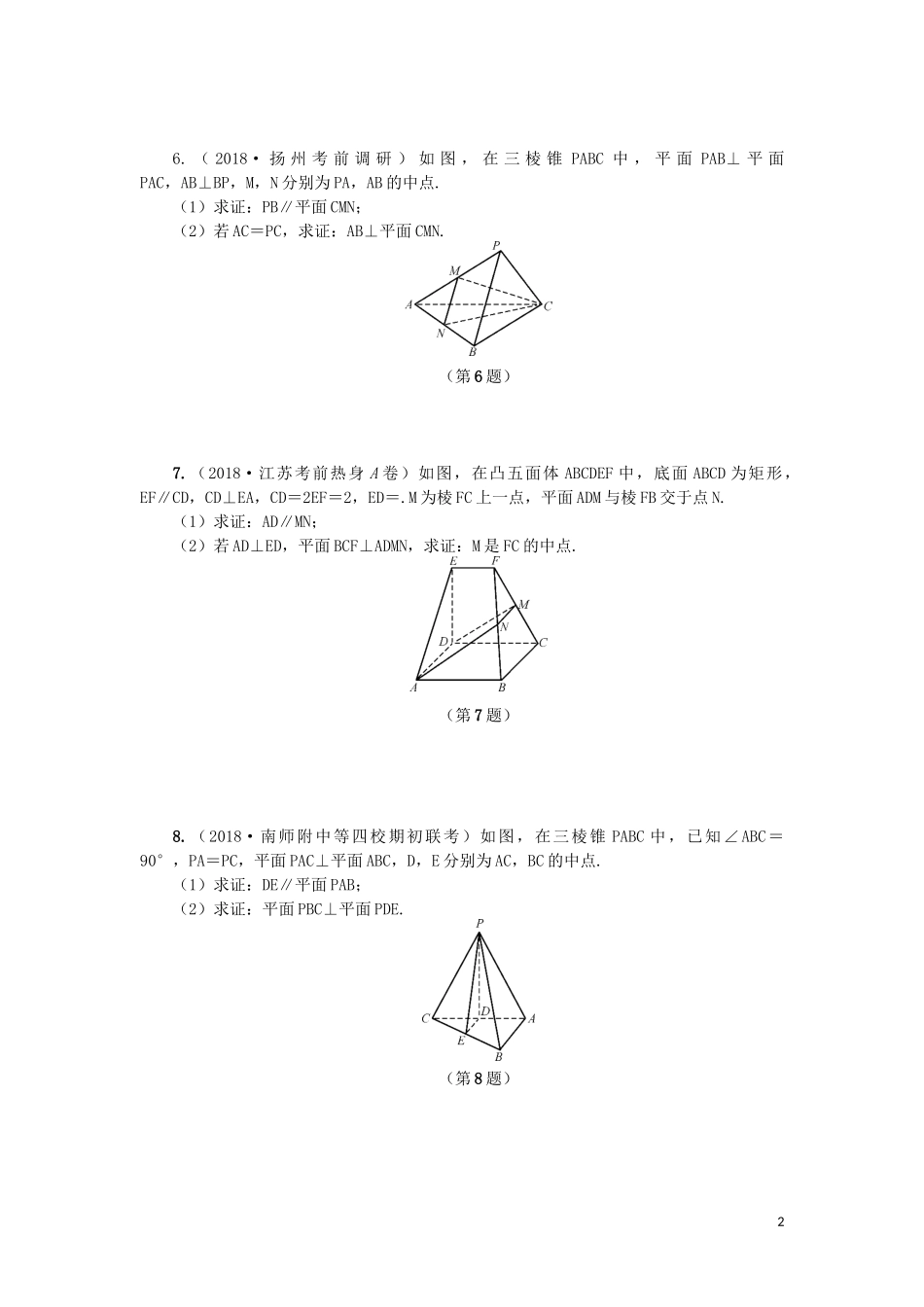
第48课直线与平面、平面与平面的垂直A.课时精练一、填空题1.已知两条不同的直线m,n,两个不重合的平面α,β,则下列命题中正确的是.(填序号)①若m⊥α,n⊥β,α⊥β,则m⊥n;②若m⊥α,n∥β,α⊥β,则m⊥n;③若m∥α,n∥β,α∥β,则m∥n;④若m∥α,n⊥β,α⊥β,则m∥n.2.已知α,β是两个不重合的平面,l,m是两条不同的直线,l⊥α,m⊂β.给出下列命题:①α∥β⇒l⊥m;②α⊥β⇒l∥m;③m∥α⇒l⊥β;④l⊥β⇒m∥α.其中正确的命题是.(填序号)3.给出下列命题:①如果一个平面经过另一个平面的垂线,那么这两个平面互相垂直;②如果一个平面内的两条直线与另一个平面都平行,那么这两个平面互相平行;③如果两条平行直线中的一条垂直于直线m,那么另一条直线也与直线m垂直;④如果两个平面垂直,那么一个平面内与它们的交线不垂直的直线与另一个平面也不垂直.其中真命题为.(填序号)4.已知m,n表示两条不同的直线,α,β,γ表示三个不重合的平面,给出下列命题:①若α∩β=m,n⊂α,n⊥m,则α⊥β;②若α⊥β,α∩γ=m,β∩γ=n,则m⊥n;③若α⊥β,α⊥γ,β∩γ=m,则m⊥α;④若m⊥α,n⊥β,m⊥n,则α⊥β.其中正确的命题是.(填序号)二、解答题5.(2018·浙江卷)如图,已知多面体ABCA1B1C1,A1A,B1B,C1C均垂直于平面ABC,∠ABC=120°,A1A=4,C1C=1,AB=BC=B1B=2,求证:AB1⊥平面A1B1C1.(第5题)16.(2018·扬州考前调研)如图,在三棱锥PABC中,平面PAB⊥平面PAC,AB⊥BP,M,N分别为PA,AB的中点.(1)求证:PB∥平面CMN;(2)若AC=PC,求证:AB⊥平面CMN.(第6题)7.(2018·江苏考前热身A卷)如图,在凸五面体ABCDEF中,底面ABCD为矩形,EF∥CD,CD⊥EA,CD=2EF=2,ED=.M为棱FC上一点,平面ADM与棱FB交于点N.(1)求证:AD∥MN;(2)若AD⊥ED,平面BCF⊥ADMN,求证:M是FC的中点.(第7题)8.(2018·南师附中等四校期初联考)如图,在三棱锥PABC中,已知∠ABC=90°,PA=PC,平面PAC⊥平面ABC,D,E分别为AC,BC的中点.(1)求证:DE∥平面PAB;(2)求证:平面PBC⊥平面PDE.(第8题)2B.滚动小练1.若f(sinα+cosα)=sinα·cosα,则函数f(x)的定义域为,f的值为.2.在等腰三角形ABC中,若∠BAC=90°,AB=AC=2,BC=2BD,AC=3AE,则AD·BE的值为.3.已知等差数列{an}的公差为d,前n项和为Sn,等比数列{bn}的公比为q,若b1=a1,b2=2,q=d,S10=100.(1)求数列{an},{bn}的通项公式;(2)当d>1时,记cn=,求数列{cn}的前n项和Tn.34