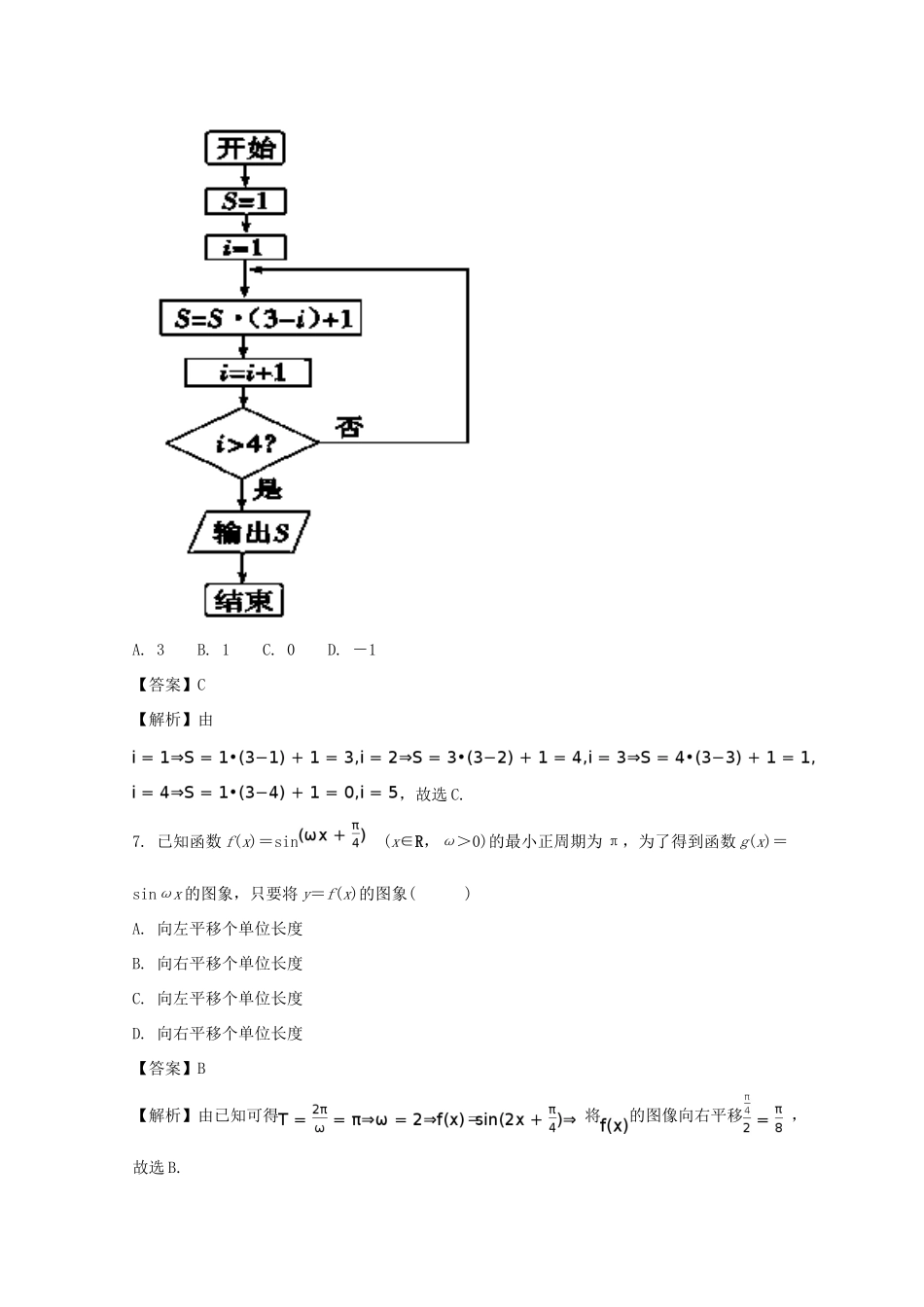
2016—2017学年下学期期末考试高一年级数学试题(文)第I卷(选择题共60分)一、选择题(本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的)1.的值是()A.B.C.D.【答案】A【解析】,故选A.2.已知,则的值是()A.B.3C.D.【答案】C【解析】由已知可得,故选C.3.甲校有3600名学生,乙校有5400名学生,丙校有1800名学生,为统计三校学生某方面的情况,计划采用分层抽样法,抽取一个容量为30人的样本,应在这三校分别抽取学生().A.30人,30人,30人B.30人,45人,15人C.20人,30人,10人D.10人,15人,5人【答案】D【解析】解:甲校、乙校、丙校的学生数比例为3600:5400:1800=2:3:1,抽取一个容量为90人的样本,应在这三校分别抽取学生90×=30人,90×=45人,90×=15人.故选B.4.已知一个样本数据按从小到大的顺序排列为13,14,19,x,23,27,28,31,中位数为22,则x的值等于().A.21B.22C.20D.23【答案】A【解析】中位数,故选A.5.对一个容量为N的总体抽取容量为n的样本,当选取简单随机抽样、系统抽样和分层抽样三种不同方法抽取样本时,总体中每个个体被抽中的概率依次为,则()A.B.C.D.【答案】D【解析】试题分析:根据随机抽样的性质可知,,故选D.考点:随机抽样.6.阅读下边的程序框图,运行相应的程序,则输出S的值为()A.3B.1C.0D.-1【答案】C【解析】由,故选C.7.已知函数f(x)=sin(x∈R,ω>0)的最小正周期为π,为了得到函数g(x)=sinωx的图象,只要将y=f(x)的图象()A.向左平移个单位长度B.向右平移个单位长度C.向左平移个单位长度D.向右平移个单位长度【答案】B【解析】由已知可得将的图像向右平移,故选B.8.设D为△ABC所在平面内一点,,则()A.B.C.D.【答案】B【解析】,故选B.9.已知向量a,b满足a⊥b,|a|=1,|b|=2,则|2a-b|=()A.0B.2C.4D.8【答案】B【解析】,故选B.10.在如图所示的茎叶图中,若甲组数据的众数为14,则乙组数据的中位数为()A.6B.8C.10D.14【答案】C【解析】由已知可得乙的中位数数为,故选C.11.已知函数f(x)=(1+cos2x)sin2x,x∈R,则f(x)是()A.最小正周期为π的奇函数B.最小正周期为的奇函数C.最小正周期为π的偶函数D.最小正周期为的偶函数【答案】D【解析】化简,且是偶函数,故选D.12.已知函数,的图像与直线的两个相邻交点的距离等于,则的单调递增区间是()A.B.C.D.【答案】A【解析】化简当,即是是增函数,故选A.第Ⅱ卷(非选择题共90分)二、填空题:本大题共4小题,每小题5分,共20分,把答案填在答题卷的横线上。13.从1,2,3,4这四个数中一次随机选取两个数,所取两个数之和为5的概率是_______.【答案】【解析】试题分析:任取两个数共有,,,,,,共个基本事件,其所取两个数和为的基本事件,,共个基本事件,所以概率,所以答案应填:.考点:古典概型.14.函数f(x)=Asin(ωx+φ)的图象如图所示,则f()=______.【答案】0【解析】由图可得.15.如图所示,在正方形内有一扇形(见阴影部分),点P随意等可能落在正方形内,则这点落在扇形外且在正方形内的概率为________.【答案】1-【解析】试题分析:设正方形边长为1,所以正方形面积为1,扇形面积为,所以点落在扇形外,且在正方形内的概率为考点:几何概型16.sin21°+sin22°+sin23°+…+sin288°+sin289°的值为________.【答案】【解析】设S=sin21°+sin22°+sin23°+…+sin289°,又 S=sin289°+sin288°+sin287°+…+sin21°=cos21°+cos22°+cos23°+…+cos289°,∴2S=89,三、解答题:本题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.17.一盒中装有12个球,其中5个红球,4个黑球,2个白球,1个绿球,从中随机取出1球,求:(Ⅰ)取出1球是红球或黑球的概率;(Ⅱ)取出1球是红球或黑球或白球的概率.【答案】(1)(2)【解析】试题分析:思路一(利用互斥事件求概率)记事件={任取球为红球},={任取球为黑球},={任取球为白球},={任取球为绿球},根据题意知,事件彼此互斥,由互斥事件的概率公式即得思路二(利用对立事件求概率)(1)由的对立事件为计算即得;(2)由的对立事件为,计算即得.试题解析:方法...