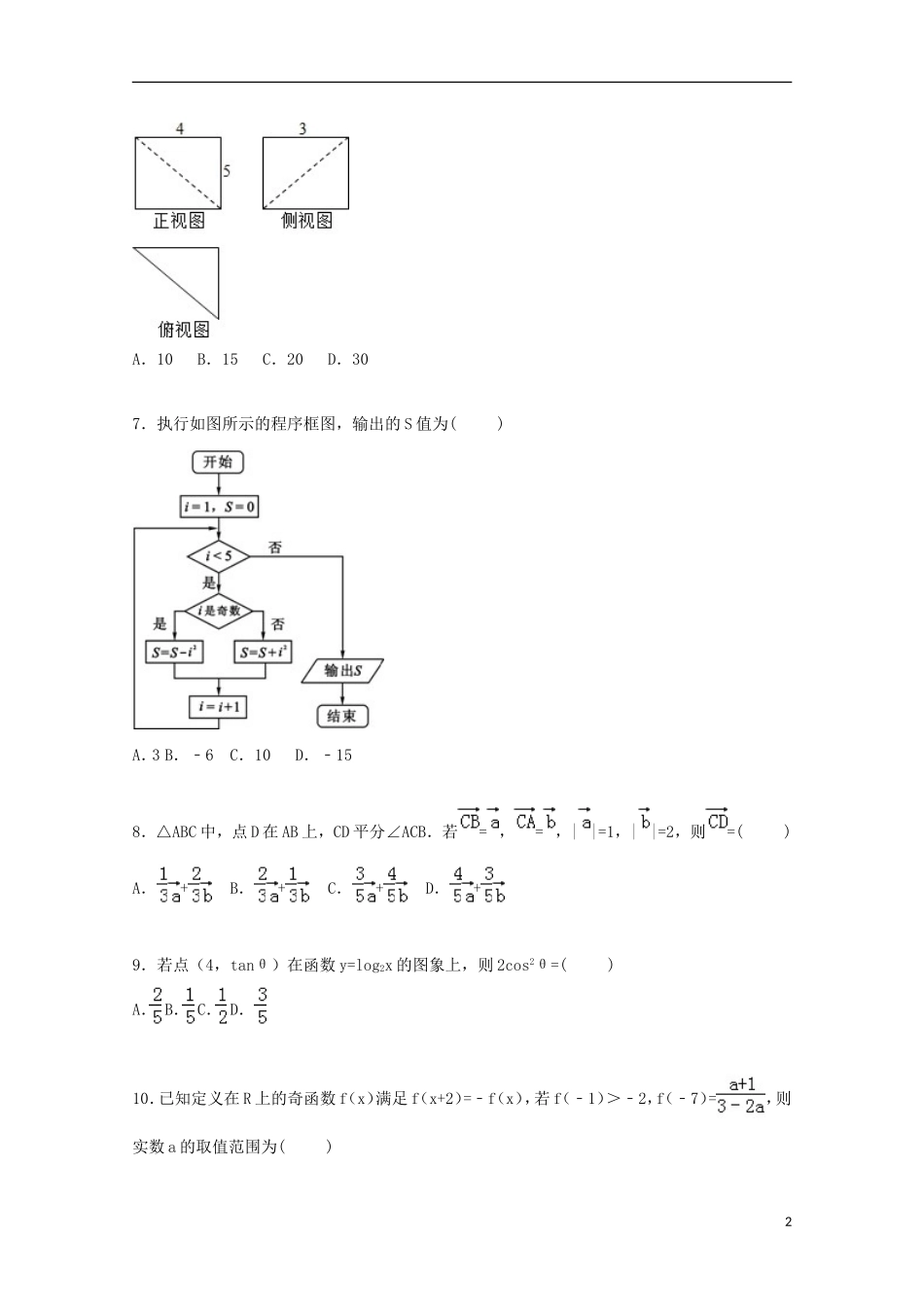
2015-2016学年河南省开封市高三(上)定位数学试卷(文科)一、选择题:本大题共12小题,每小题5分,在每小题给出的四个选项中,只有一项是符合题目要求的.1.设集合U={0,1,2,3,4,5},集合A={1,2},B={2,4}则∁U(A∪B)=()A.{1,2,4}B.{0,3,5}C.{0,1,3,4,5}D.∅2.若复数Z=(a∈R,i是虚数单位)是纯虚数,则在复平面内Z对应点的坐标为()A.(0,2)B.(0,3i)C.(0,3)D.(0,2i)3.下列命题正确的是()A.已知p:>0,则﹣p:≤0B.存在实数x∈R,使sinx+cosx=成立C.命题p:对任意的x∈R,x2+x+1>0,则﹣p:对任意的x∈R,x2+x+1≤0D.若p或q为假命题,则p,q均为假命题4.把函数图象上各点的横坐标缩短到原来的倍(纵坐标不变),再将图象向右平移个单位,那么所得图象的一条对称轴方程为()A.B.C.D.5.我国古代数学名著《九章算术》有“米谷粒分”题:粮仓开仓收粮,有人送来米1534石,验得米内夹谷,抽样取米一把,数得254粒内夹谷28粒,则这批米内夹谷约为()A.134石B.169石C.338石D.1365石6.某空间几何体的三视图如图所示,则此几何体的体积为()1A.10B.15C.20D.307.执行如图所示的程序框图,输出的S值为()A.3B.﹣6C.10D.﹣158.△ABC中,点D在AB上,CD平分∠ACB.若=,=,||=1,||=2,则=()A.+B.+C.+D.+9.若点(4,tanθ)在函数y=log2x的图象上,则2cos2θ=()A.B.C.D.10.已知定义在R上的奇函数f(x)满足f(x+2)=﹣f(x),若f(﹣1)>﹣2,f(﹣7)=,则实数a的取值范围为()2A.B.(﹣2,1)C.D.11.若曲线y=与曲线y=alnx在它们的公共点P(s,t)处具有公共切线,则实数a=()A.﹣2B.C.1D.212.已知椭圆(a>b>0)的半焦距为c(c>0),左焦点为F,右顶点为A,抛物线与椭圆交于B、C两点,若四边形ABFC是菱形,则椭圆的离心率是()A.B.C.D.二.本卷包括必考题和选考题两部分,第(13)题~第(21)题为必考题,每个试题考生都必须作答,第(22)题~第(24)题为选考题,考试根据要求作答.填空题:本大题共4小题,每小题5分.13.若x,y满足约束条件,则z=3x﹣y的最小值是__________.14.已知函数f(x)=,则f=__________.15.设直线2x+3y+1=0和圆x2+y2﹣2x﹣3=0相交于点A、B,则弦AB的垂直平分线方程是__________.16.在△ABC中,若(sinA+sinB):(sinA+sinC):(sinB+sinC)=4:5:6,且该三角形面积为,则△ABC的最大边长等于__________.3三、解答题:解答应写出文字说明,证明过程和演算步骤17.已知递增等差数列{an}中,a1=1,a1,a4,a10成等比数列.(Ⅰ)求数列{an}的通项公式;(Ⅱ)求数列{an•3n}的前n项和Sn.18.某电子广告牌连续播出四个广告,假设每个广告所需的时间互相独立,且都是整数分钟,经统计,以往播出100次所需的时间(t)的情况如下:类别1号广告2号广告3号广告4号广告广告次数20304010时间t(分钟/人)2346每次随机播出,若将频率视为概率.(Ⅰ)求恰好在开播第6分钟后开始播出第3号广告的概率;(Ⅱ)求第4分钟末完整播出广告1次的概率.19.在四棱锥P﹣ABCD中,底面ABCD为直角梯形,AD∥BC,AB⊥BC侧面PAB⊥底面ABCD,PA=AD=AB=2,BC=4,∠PAB=60°(I)若PE中点为.求证:AE∥平面PCD;(Ⅱ)若G是PC的中点,求三棱锥P﹣BDG的体积.20.已知,椭圆C:+=1(m>n>0)短轴长是1,离心率e=.(Ⅰ)求椭圆C的方程;(Ⅱ)过F(﹣,0)的直线交椭圆C于点M,N,G(,0),求△GMN面积的最大值.421.已知函数f(x)=alnx+x2﹣1(1)求曲线y=f(x)在点(1,f(1))处的切线方程;(2)若关于x的不等式f(x)≥b(x﹣1)在22.如图,已知AB为⊙O的直径,CE⊥AB于点H,与⊙O交于点C、D,且AB=10,CD=8,DE=4,EF与⊙O切于点F,BF与HD交于点G.(Ⅰ)证明:EF=EG;(Ⅱ)求GH的长.23.在平面直角坐标系xoy中,以O为极点,x轴的正半轴为极轴的极坐标系中,直线l的极坐标方程为θ=,曲线C的参数方程为.(1)写出直线l与曲线C的直角坐标方程;(2)过点M平行于直线l1的直线与曲线C交于A、B两点,若|MA|•|MB|=,求点M轨迹的直角坐标方程.524.已知函数f(x)=|2x﹣a|+|2x+3|...