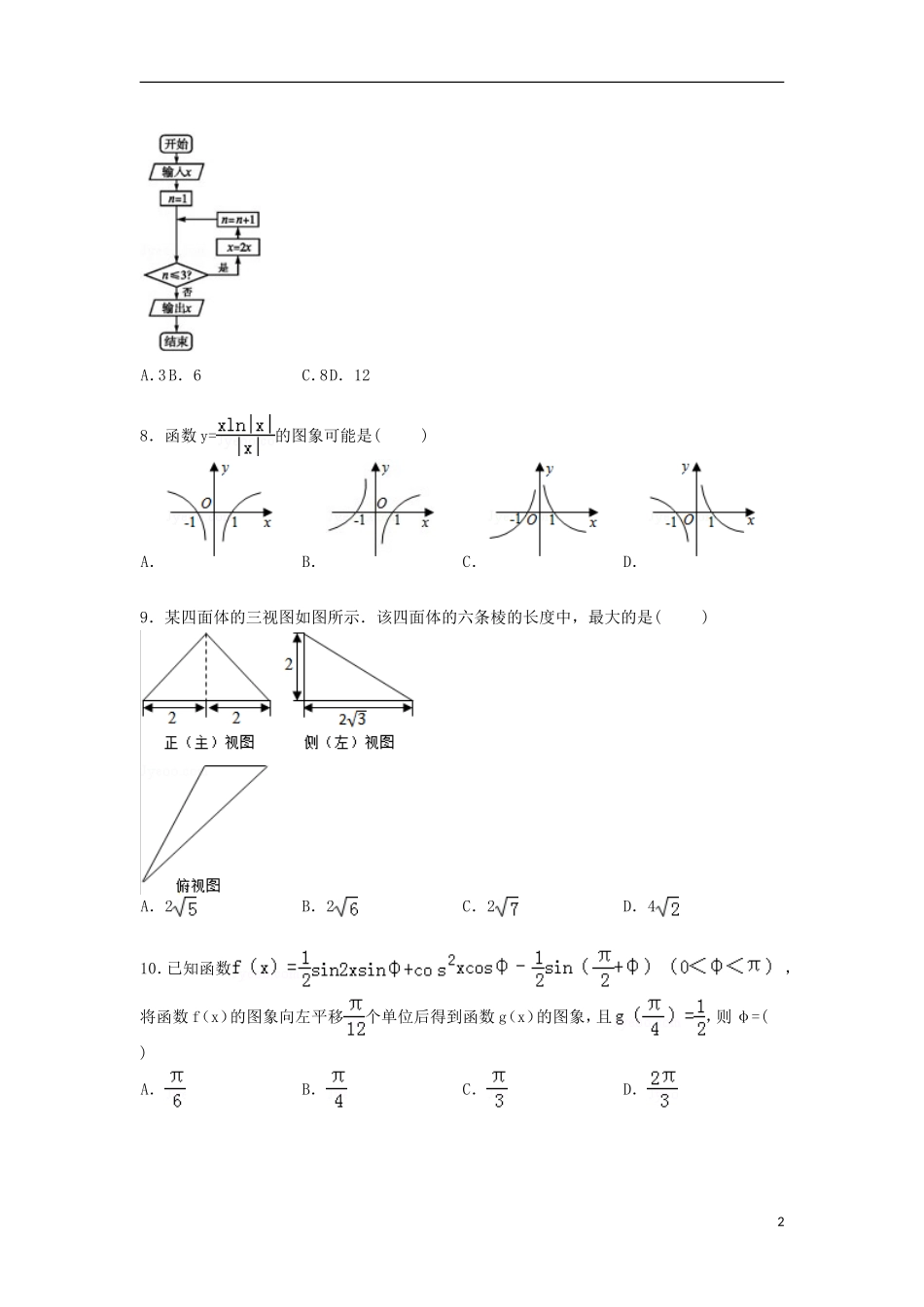
吉林省延边州2015届高考数学一模试卷(理科)一、选择题:本大题共12小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是符合题目要求的1.复数z=(1+2i)i,则复数z的共轭复数在复平面内对应的点的坐标为()A.(﹣2,1)B.(2,﹣1)C.(2,1)D.(﹣2,﹣1)2.已知集合A={x|2x﹣1≥4},B={x|x2﹣2x﹣3<0},则A∩(∁RB)等于()A.{x|x≥3}B.{x|x>3}C.{x|﹣1<x<3}D.{x|x≥3或x≤﹣1}3.双曲线﹣=1(a>0,b>0)的离心率为2,则其渐近线的方程为()A.y=±xB.y=±xC.y=±xD.y=±2x4.等差数列{an}的前n项和为Sn,且S3=6,a3=4,则公差d等于()A.1B.C.2D.35.为了了解某学校1500名高中男生的身体发育情况,抽查了该校100名高中男生的体重情况.根据所得数据画出样本的频率分布直方图,据此估计该校高中男生体重在70~78kg的人数为()A.240B.210C.180D.606.已知两个单位向量,的夹角为60°,=(1﹣t)+t,若•=﹣,则实数t的取值是()A.2B.﹣2C.D.﹣7.执行如图所示程序框图所表达的算法,若输出的x值为48,则输入的x值为()1A.3B.6C.8D.128.函数y=的图象可能是()A.B.C.D.9.某四面体的三视图如图所示.该四面体的六条棱的长度中,最大的是()A.2B.2C.2D.410.已知函数,将函数f(x)的图象向左平移个单位后得到函数g(x)的图象,且,则φ=()A.B.C.D.211.抛物线y2=2px(p>0)的焦点为F,已知点A,B为抛物线上的两个动点,且满足∠AFB=120°.过弦AB的中点M作抛物线准线的垂线MN,垂足为N,则的最小值为()A.B.C.1D.12.已知≤k<1,函数f(x)=|2x﹣1|﹣k的零点分别为x1,x2(x1<x2),函数g(x)=|2x﹣1|的零点分别为x3,x4(x3<x4),则(x4﹣x3)+(x2﹣x1)的最小值为()A.1B.log23C.log26D.3二、填空题:本大题共4小题,每小题5分,共20分,把答案填在题中的横线上.13.在(x﹣)6的二项式展开式中,常数项等于__________.14.设变量x,y满足约束条件,则z=x﹣3y的最小值__________.15.正三角形ABC的三个顶点都在半径为2的球面上,球心O到平面ABC的距离为1,点D是线段BC的中点,过D作球O的截面,则截面面积的最小值为__________.16.设△AnBnCn的三边长分别为an,bn,cn,n=1,2,3…,若b1>c1,b1+c1=2a1,an+1=an,bn+1=,cn+1=,则∠An的最大值是__________.三、解答题:本大题共5小题,共70分,解答应写出文字说明、证明过程或演算步骤17.在△ABC中,角A,B,C(C为钝角)所对的边分别为a,b,c,且cos(A+B﹣C)=,a=2,=2.(1)求cosC的值;3(2)求b的长.18.如图,三棱锥P﹣ABC中,PB⊥底面ABC于B,∠BCA=90°,PB=CA=2,点E是PC的中点.(1)求证:侧面PAC⊥平面PBC;(2)若异面直线AE与PB所成的角为θ,且,求二面角C﹣AB﹣E的大小.19.某单位有车牌尾号为2的汽车A和尾号为6的汽车B,两车分属于两个独立业务部门.对一段时间内两辆汽车的用车记录进行统计,在非限行日,A车日出车频率0.6,B车日出车频率0.5.该地区汽车限行规定如下:车尾号0和51和62和73和84和9限行日星期一星期二星期三星期四星期五现将汽车日出车频率理解为日出车概率,且A,B两车出车相互独立.(Ⅰ)求该单位在星期一恰好出车一台的概率;(Ⅱ)设X表示该单位在星期一与星期二两天的出车台数之和,求X的分布列及其数学期望E(X).20.已知椭圆C:+=1(a>b>0)的左右焦点和短轴的两个端点构成边长为2的正方形.(1)求椭圆C的方程;(2)过点Q(1,0)的直线l与椭圆C相较于A,B两点,且点P(4,3),记直线PA,PB的斜率分别为k1,k2,当k1•k2取最大值时,求直线l的方程.21.已知函数f(x)=(2﹣a)(x﹣1)﹣2lnx,g(x)=xe1﹣x(a∈R,e为自然对数的底).(1)当a=1时,求f(x)的单调区间;(2)若对任意的x0∈(0,e],在(0,e]上存在两个不同的xi(i=1,2),使得f(xi)=g(x0)成立,求a的取值范围.四、选做题:请考生在22、23、24三题中任选一题作答,如果多选,则按所做的第一题计分【选修4-1:几何证明选讲】22.如图,△ABO三边上的点C、D、E都在⊙O上,已知AB∥DE,AC=CB.(l)求证:直线AB是⊙...