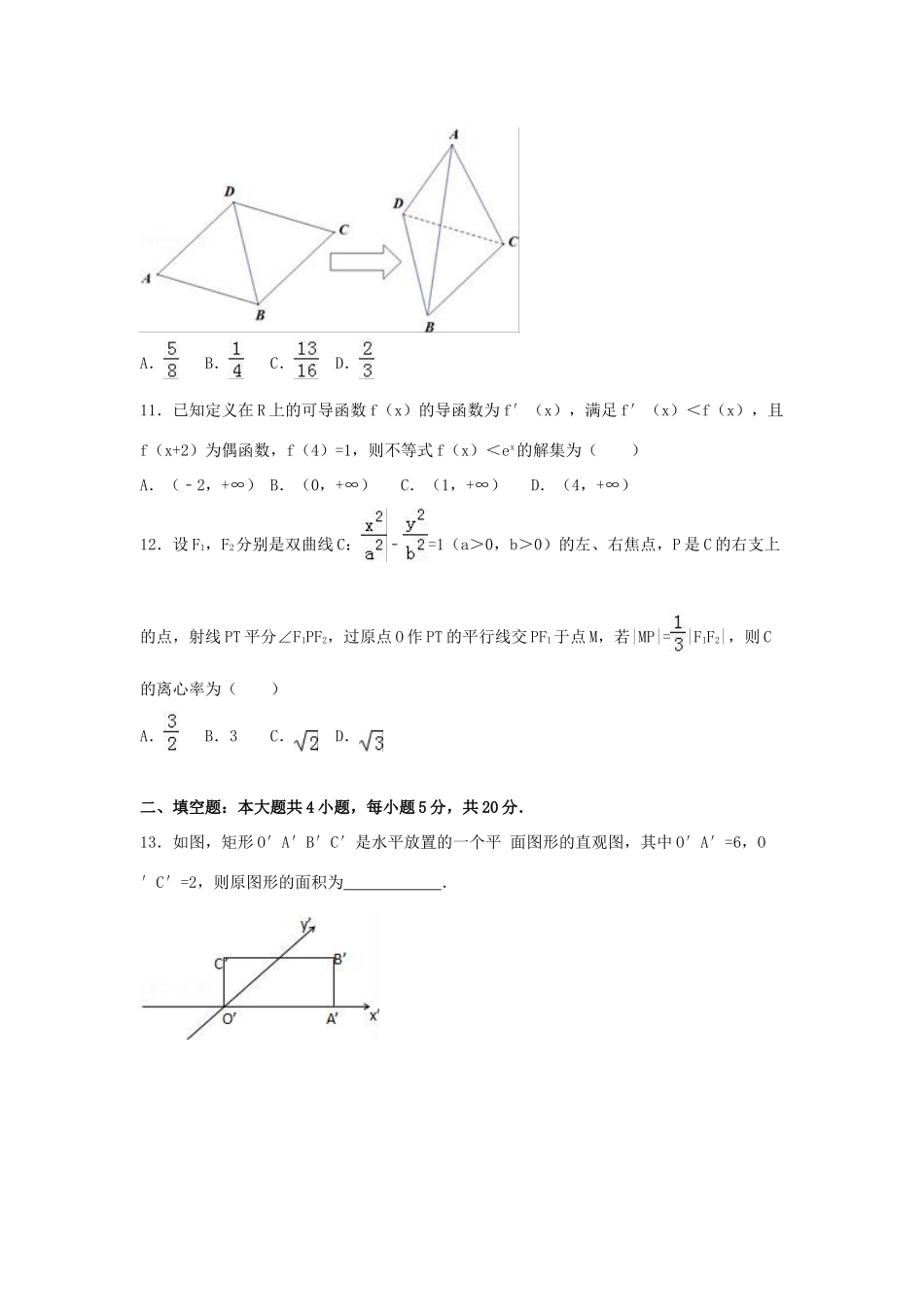
2016年河南省南阳一中高考数学三模试卷(文科)一、选择题:(本大题共12小题,每小题5分)1.定义集合A={x|2x≥1}},B={x|x<0},则A∩∁RB=()A.(1,+∞)B.[0,1]C.[0,1)D.[0,2)2.若复数z满足z(1﹣i)=|1﹣i|+i,则z的实部为()A.B.﹣1C.1D.3.设命题p:“若ex>1,则x>0”,命题q:“若a>b,则”,则()A.“p∧q”为真命题B.“p∨q”为真命题C.“¬p”为真命题D.以上都不对4.双曲线C:x2﹣=1的顶点到渐近线的距离与焦点到渐近线的距离之比为()A.B.C.D.5.若向量,满足||=||=2,与的夹角为60°,在+上的投影等于()A.B.2C.D.4+26.过点A(a,a)可作圆x2+y2﹣2ax+a2+2a﹣3=0的两条切线,则实数a的取值范围为()A.a<﹣3或a>1B.a<C.﹣3<a<1或a>D.a<﹣3或1<a<7.函数f(x)=Asin(ωx+φ)(其中A>0,ω>0,|φ|<)的图象如图所示,为了得到y=cos2x的图象,则只要将f(x)的图象()A.向左平移个单位长度B.向右平移个单位长度C.向左平移个单位长度D.向右平移个单位长度8.执行如图所示的程序框图.若输入a=3,则输出i的值是()A.2B.3C.4D.59.已知{an}是等差数列,公差d不为零,前n项和是Sn,若a3,a4,a8成等比数列,则()A.a1d>0,dS4>0B.a1d<0,dS4<0C.a1d>0,dS4<0D.a1d<0,dS4>010.如图,边长为1的菱形ABCD中,∠DAB=60°,沿BD将△ABD翻折,得到三棱锥A﹣BCD,则当三棱锥A﹣BCD体积最大时,异面直线AD与BC所成的角的余弦值为()A.B.C.D.11.已知定义在R上的可导函数f(x)的导函数为f′(x),满足f′(x)<f(x),且f(x+2)为偶函数,f(4)=1,则不等式f(x)<ex的解集为()A.(﹣2,+∞)B.(0,+∞)C.(1,+∞)D.(4,+∞)12.设F1,F2分别是双曲线C:﹣=1(a>0,b>0)的左、右焦点,P是C的右支上的点,射线PT平分∠F1PF2,过原点O作PT的平行线交PF1于点M,若|MP|=|F1F2|,则C的离心率为()A.B.3C.D.二、填空题:本大题共4小题,每小题5分,共20分.13.如图,矩形O′A′B′C′是水平放置的一个平面图形的直观图,其中O′A′=6,O′C′=2,则原图形的面积为.14.若不等式x2+y2≤2所表示的区域为M,不等式组表示的平面区域为N,现随机向区域N内抛一粒豆子,则豆子落在区域M内的概率为.15.在△ABC中,已知tan=sinC,给出以下四个论断:①tanA•cotB=1②0<sinA+sinB≤③sin2A+cos2B=1④cos2A+cos2B=sin2C,其中正确的是.16.已知O为△ABC的垂心,且+2+3=,则A角的值为.三、解答题(本大题共5小题,共70分,解答题写出必要的文字说明、推理和演算步骤.)17.已知数列{bn}的前n项和.(Ⅰ)求数列{bn}的通项公式;(Ⅱ)设数列{an}的通项,求数列{an}的前n项和Tn.18.某工厂有工人500名,记35岁以上(含35岁)的为A类工人,不足35岁的为B类工人,为调查该厂工人的个人文化素质状况,现用分层抽样的方法从A、B两类工人中分别抽取了40人、60人进行测试.(I)求该工厂A、B两类工人各有多少人?(Ⅱ)经过测试,得到以下三个数据图表:(茎、叶分别是十位和个位上的数字)(如图)表:100名参加测试工人成绩频率分布表组号分组频数频率1[55,60)50.052[60,65)200.203[65,70)4[70,75)350.355[75,80)6[80,85)合计1001.00①先填写频率分布表中的六个空格,然后将频率分布直方图(图二)补充完整;②该厂拟定从参加考试的79分以上(含79分)的B类工人中随机抽取2人参加高级技工培训班,求抽到的2人分数都在80分以上的概率.19.已知某几何体的直观图和三视图如图所示,其正视图为矩形,侧视图为等腰直角三角形,俯视图为直角梯形.(1)求证:BN丄平面C1B1N;(2)设M为AB中点,在BC边上找一点P,使MP∥平面CNB1,并求的值.(3)求点A到平面CB1N的距离.20.在平面直角坐标系xOy中,一动圆经过点(,0)且与直线x=﹣相切,设该动圆圆心的轨迹为曲线E.(Ⅰ)求曲线E的方程;(Ⅱ)设P是曲线E的动点,点B、C在y轴上,△PBC的内切圆的方程为(x﹣1)2+y2=1,求△PBC面积的最小值.21.已知函数f(x)=lnx.(1)若曲线g(x)=f(x)+﹣1在点(2,g(2))处...