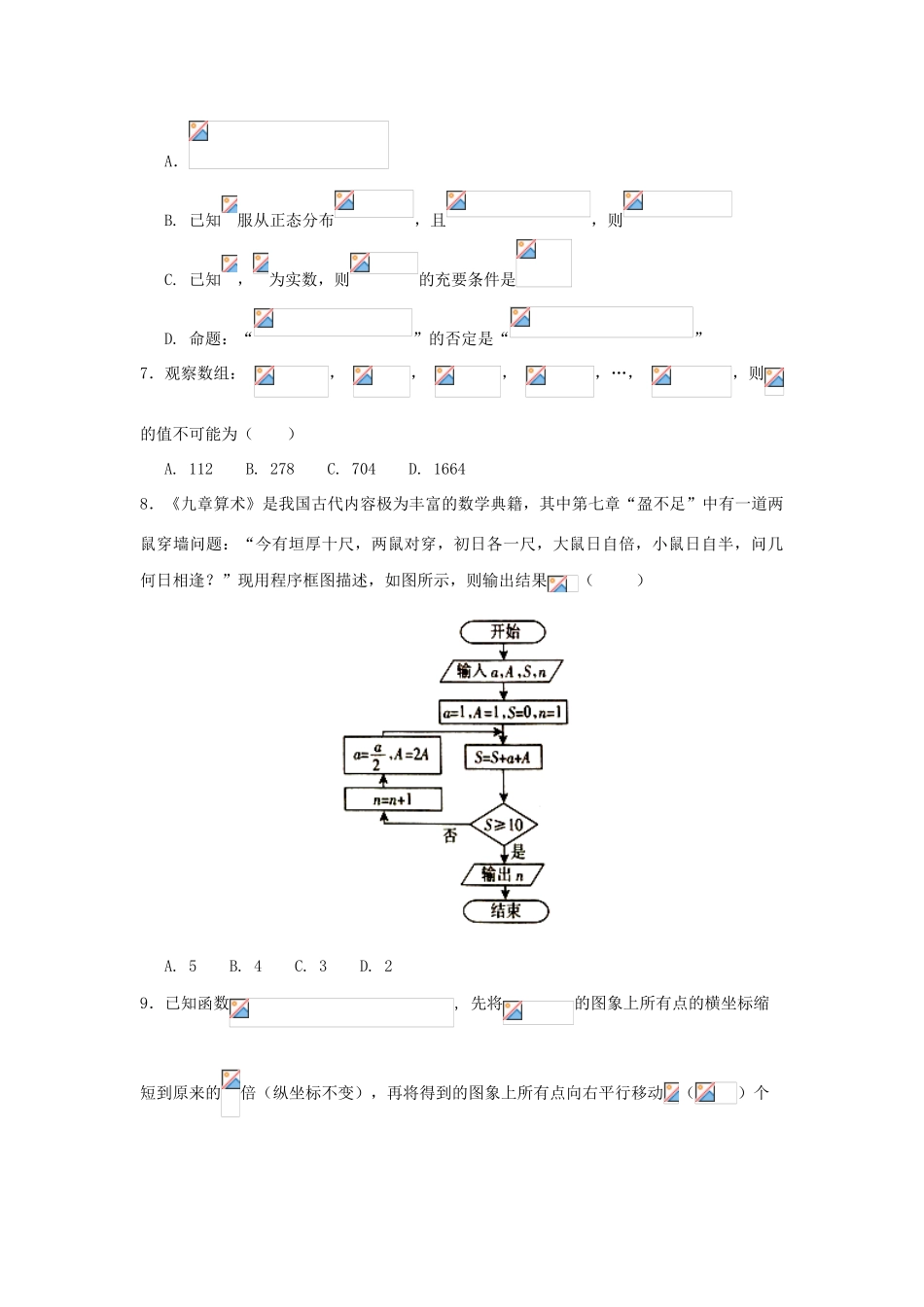
江西省七校2018届高三数学第一次联考试题理一.选择题:本大题共12小题,每小题5分,在每小题给出的四个选项中,只有一项是符合题目要求的.1.在右边图中,设全集集合分别用椭圆内图形表示,若集合,则阴影部分图形表示的集合为A.B.C.D.2.已知复数(为虚数单位),则的虚部()A.1B.-1C.iD.-i3.若,则下列结论不正确的是A.B.C.D.4.已知,是两条不同直线,是一个平面,则下列命题中正确的是()A.若,,则B.若,,则C.若,,则D.若,,则5.在斜三角形ABC中,()A.1B.C.2D.6.下列命题中,正确的是()A.B.已知服从正态分布,且,则C.已知,为实数,则的充要条件是D.命题:“”的否定是“”7.观察数组:,,,,…,,则的值不可能为()A.112B.278C.704D.16648.《九章算术》是我国古代内容极为丰富的数学典籍,其中第七章“盈不足”中有一道两鼠穿墙问题:“今有垣厚十尺,两鼠对穿,初日各一尺,大鼠日自倍,小鼠日自半,问几何日相逢?”现用程序框图描述,如图所示,则输出结果()A.5B.4C.3D.29.已知函数,先将的图象上所有点的横坐标缩短到原来的倍(纵坐标不变),再将得到的图象上所有点向右平行移动()个单位长度,得到的图象关于直线对称,则的最小值为()A.B.C.D.10.已知为双曲线:(,)的右焦点,,为的两条渐近线,点在上,且,点在上,且,若,则双曲线的离心率为()A.B.C.或D.或11.如图,梯形中,,,,,和分别为与的中点,对于常数,在梯形的四条边上恰好有8个不同的点,使得成立,则实数的取值范围是()A.B.C.D.12.已知函数,关于的不等式只有两个整数解,则实数的取值范围是A.B.C.D.二、填空题(每小题5分,共20分)13.设,则二项式的展开式中含项的系数为__________.14.设满足约束条件,若的最小值为,则的值为.15.设、、、为自然数、、、的一个全排列,且满足,则这样的排列有________个.16.已知正六棱柱的顶点都在同一个球面上,且该六棱柱的体积为,当球的体积最小时,正六棱柱底面边长为.三、解答题(17题10分,其余每题12分,共70分)17.如图,在中,已知点在边上,,,,.(1)求的值;(2)求的长.18.已知数列满足(Ⅰ)求数列的通项公式;(Ⅱ)若,求数列的前项和.19.(本小题满分12分)为了解患肺心病是否与性别有关,在某医院对入院者用简单随机抽样方法抽取50人进行调查,结果如下列联表:(Ⅰ)是否有的把握认为入院者中患肺心病与性别有关?请说明理由;(Ⅱ)已知在患肺心病的10位女性中,有3位患胃病.现在从这10位女性中,随机选出3名进行其它方面的排查,记选出患胃病的女性人数为,求的分布列和数学期望;附:0.150.100.050.0250.0100.0050.0012.0722.7063.8415.0246.6357.87910.828.20.(本小题满分12分)有一个侧面是正三角形的四棱锥如图(1),它的三视图如图(2).(Ⅰ)证明:平面;(Ⅱ)求平面与正三角形侧面所成二面角的余弦值.21、已知椭圆C的中心在原点,焦点在轴上,离心率等于,它的一个顶点恰好是抛物线的焦点。(1)求椭圆C的标准方程。(2)已知点在椭圆C上,点A、B是椭圆C上不同于P、Q的两个动点,且满足:。试问:直线AB的斜率是否为定值?请说明理由。22.已知函数.(1)当,时,讨论函数在区间上零点的个数;(2)当时,如果函数恰有两个不同的极值点,,证明:.江西省红色七校2018届高三第一次联考数学理科答案一.选择题:本大题共12小题,每小题5分,在每小题给出的四个选项中,只有一项是符合题目要求的.1-5DADCB6-10BBBAD11-12DC二、填空题(每小题5分,共20分)13.19214.15.916.17.解:(1)在中,,,所以.………………………(2分)同理可得,.……………………………………(3分)所以.………(5分)(2)在中,由正弦定理得,.………(7分)又,所以.………………………………(8分)又在中,由余弦定理得,.……(10分)18.(Ⅰ);(5分)(Ⅱ).(7分)19.(Ⅰ)因为,所以,…………………………(2分)又10.828,且,………………………………(3分)故,我们有的把握认为入院者中患肺心病是与性别有关系的.………………………(5分)(Ⅱ)的所有可能取值:0,1,2,3,,,………………………………...