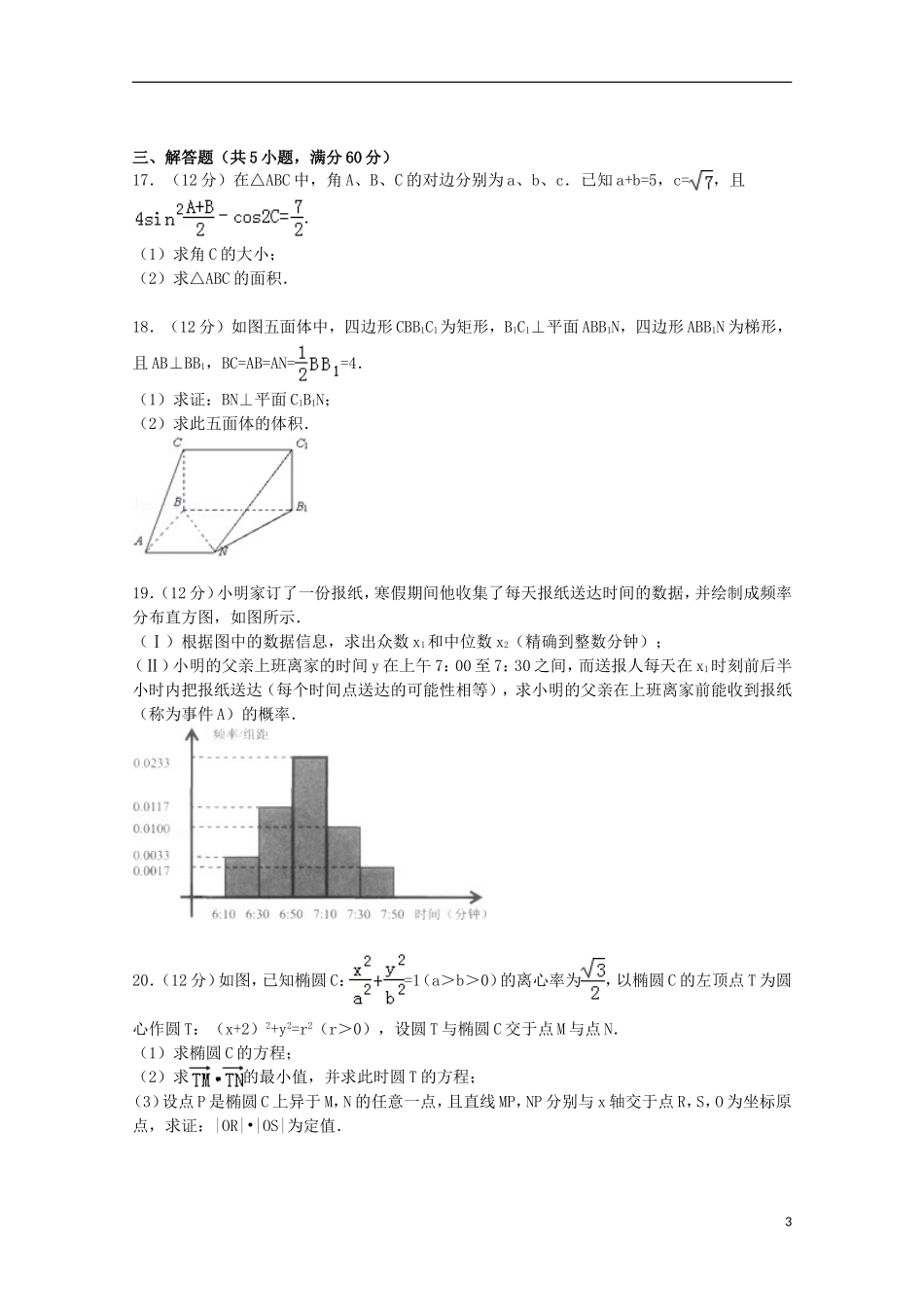
新疆维吾尔自治区喀什地区2015届高三上学期10月月考数学试卷(文科)一、选择题(本大题共12小题,每小题5分,共50分。在每小题给出的四个选项中,只有一项是符合题目要求的。1.(5分)若集合A={0,2,3,5},则集合A的真子集共有()A.7个B.8个C.15个D.16个2.(5分)复数的共轭复数为()A.B.C.D.3.(5分)“φ=”是“cosφ=0”的()A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件4.(5分)已知=(3,1),=(x,﹣1),且∥,则x等于()A.B.﹣C.3D.﹣35.(5分)在数列{an}中,a1=0,,则a2013=()A.B.C.0D.6.(5分)[理]一个袋子里装有编号为1,2,…,12的12个相同大小的小球,其中1到6号球是红色球,其余为黑色球.若从中任意摸出一个球,记录它的颜色和号码后再放回到袋子里,然后再摸出一个球,记录它的颜色和号码,则两次摸出的球都是红球,且至少有一个球的号码是偶数的概率是()A.B.C.D.7.(5分)将边长为1的正方形以其一边所在直线为旋转轴旋转一周,所得几何体的侧面积是()A.4πB.3πC.2πD.π8.(5分)如图是求函数值的算法流程图,当输入值为2时,则输出值为()1A.4B.0C.1D.﹣39.(5分)设a=log23,b=log46,c=log89,则下列关系中正确的是()A.a>b>cB.a>c>bC.c>b>aD.c>a>b10.(5分)过点P(﹣2,m)和Q(m,4)的直线的倾斜角为,则m值为()A.1B.4C.1或3D.1或411.(5分)已知a>b>0,椭圆C1的方程为+=1,双曲线C2的方程为﹣=1,C1与C2的离心率之积为,则C2的渐近线方程为()A.x±y=0B.x±y=0C.x±2y=0D.2x±y=012.(5分)a,b,c∈R+,设S=,则下列判断中正确的是()A.0<S<1B.1<S<2C.2<S<3D.3<S<4二、填空题(本大题共4小题,每小题5分)13.(5分)在正方形ABCD中,点E为AD的中点,若在正方形ABCD内部随机取一个点Q,则点Q落在△ABE内部的概率是.14.(5分)△ABC的内角A,B,C的对边分别为a,b,c,已知b=2,B=,C=,则△ABC的面积为.15.(5分)已知f(x)=ax2+bx+3a+b是偶函数,且其定义域为[a﹣1,2a],则y=f(x)的值域为.16.(5分)已知数列{an}为等差数列,若<﹣1,且它们的前n项和Sn有最大值,则使Sn>0的n的最大值为.2三、解答题(共5小题,满分60分)17.(12分)在△ABC中,角A、B、C的对边分别为a、b、c.已知a+b=5,c=,且.(1)求角C的大小;(2)求△ABC的面积.18.(12分)如图五面体中,四边形CBB1C1为矩形,B1C1⊥平面ABB1N,四边形ABB1N为梯形,且AB⊥BB1,BC=AB=AN==4.(1)求证:BN⊥平面C1B1N;(2)求此五面体的体积.19.(12分)小明家订了一份报纸,寒假期间他收集了每天报纸送达时间的数据,并绘制成频率分布直方图,如图所示.(Ⅰ)根据图中的数据信息,求出众数x1和中位数x2(精确到整数分钟);(Ⅱ)小明的父亲上班离家的时间y在上午7:00至7:30之间,而送报人每天在x1时刻前后半小时内把报纸送达(每个时间点送达的可能性相等),求小明的父亲在上班离家前能收到报纸(称为事件A)的概率.20.(12分)如图,已知椭圆C:=1(a>b>0)的离心率为,以椭圆C的左顶点T为圆心作圆T:(x+2)2+y2=r2(r>0),设圆T与椭圆C交于点M与点N.(1)求椭圆C的方程;(2)求的最小值,并求此时圆T的方程;(3)设点P是椭圆C上异于M,N的任意一点,且直线MP,NP分别与x轴交于点R,S,O为坐标原点,求证:|OR|•|OS|为定值.321.(12分)已知函数f(x)=x+sinx.(1)设P,Q是函数f(x)的图象上相异的两点,证明:直线PQ的斜率大于0;(2)求实数a的取值范围,使不等式f(x)≥axcosx在上恒成立.四、选做题请考生在第22,23,24题中任选一题做答,如多做,则按所做的第一题计分。22.(10分)已知△ABC的三个顶点的坐标为A(1,1),B(3,2),C(5,4)(1)求边AB上的高所在直线的方程;(2)若直线l与AC平行,且在x轴上的截距比在y轴上的截距大1,求直线l与两条坐标轴围成的三角形的周长.23.设函数f(x)=,其中a∈R.(1)若a=1,f(x)的定义域为区间[0,3],求f(x)的最大值和最小值;(2)若f(x)的定义...