江苏省昆山震川高级中学高三数学 全等形与相似形练习 苏科版VIP免费

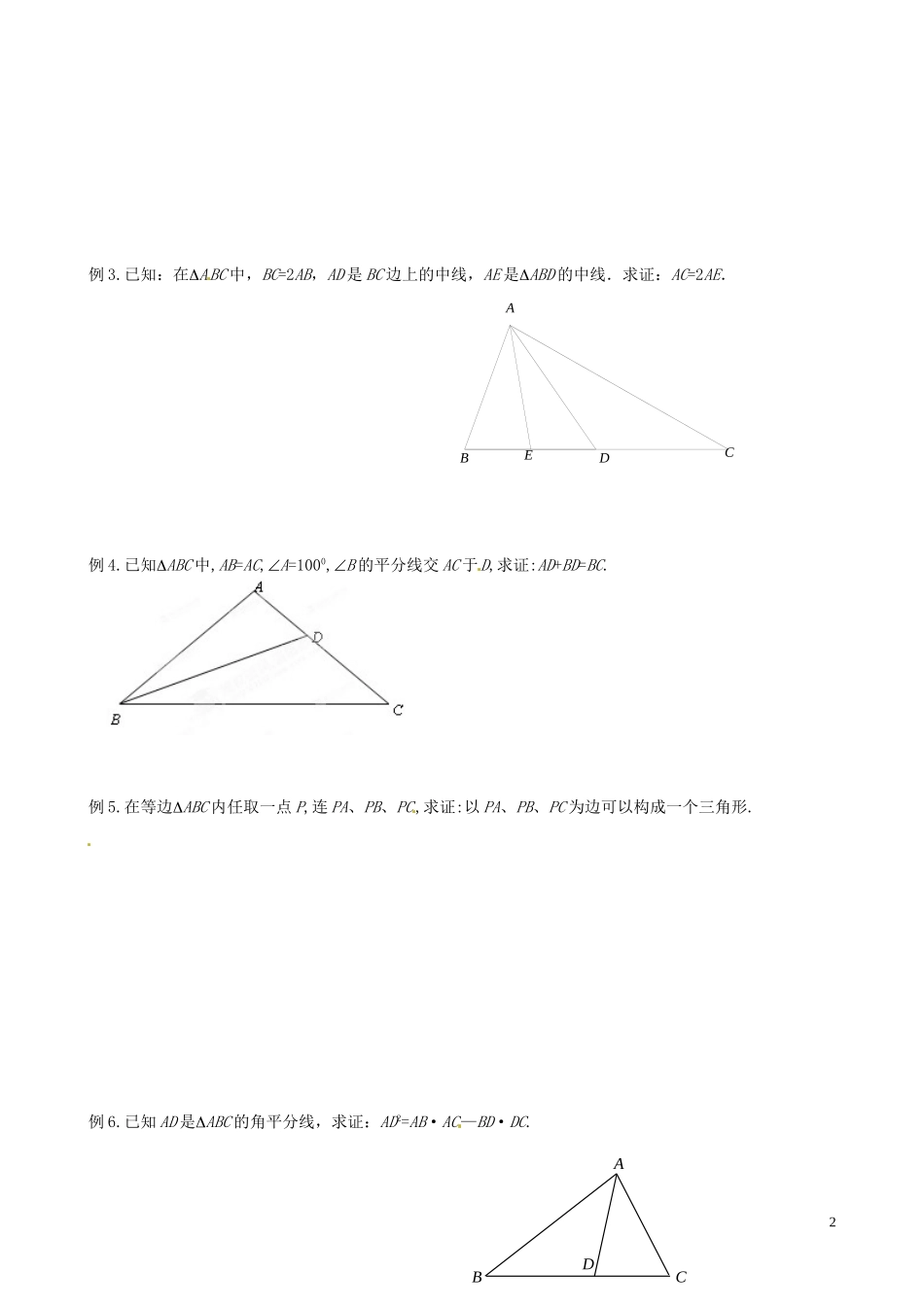
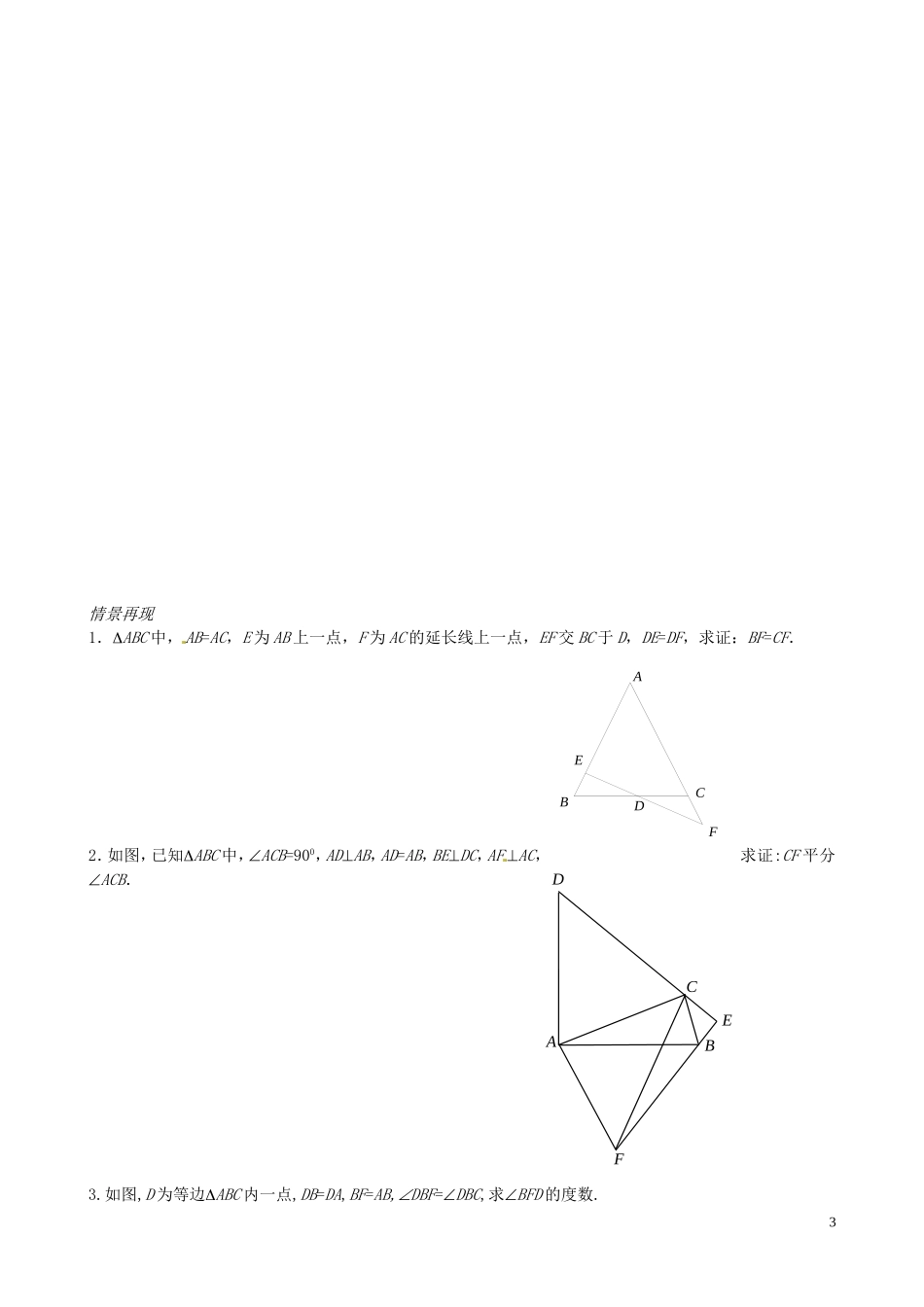
江苏省昆山震川高级中学高三数学全等形与相似形练习苏科版全等形和相似形是平面几何的重点内容，全等三角形和相似三角形是其中的主要内容．全等三角形是相似三角形的特殊情形，这两部分知识在中学数学中占有重要地位，同时这两部分知识也是研究几何的基础，它对进一步的学习和对思维能力的培养都是非常重要的．1.全等三角形的判定与性质判定边角边公理SAS、角边角公理ASA、角角边定理AAS、边边边定理SSS.若三角形是直角三角形还可以用斜边直角边定理HL.性质全等三角形的对应边、对应角、对应中线、对应高、对应角平分线、对应位置上的线段和角都相等．2.相似三角形的判定与性质判定①一个角对应相等，并且夹这个角的两边对应成比例；②两个角对应相等；③三条边对应成比例；④两个直角三角形的斜边和一条直角边对应成比例．性质相似三角形的对应角相等；对应边的比、对应中线的比、对应高的比、对应角平分线的比以及周长之比都等于相似比，面积的比等于相似比的平方．3.常用方法论证的过程通常是，由待证明的等式反过来找相应的三角形，然后证明相应的三角形全等或相似．而“相应的三角形”往往不是现成的，需要我们去构造，去作辅助线．在竞赛中，连续证多次全等或相似是常见的．例2.已知在等腰直角ABC中，A是直角，D是AC上一点，AEBD，AE的延长线交BC于F，若ADB=FDC，求证:D是AC的中点．1BCDAEF例3.已知：在ABC中，BC=2AB，AD是BC边上的中线，AE是ABD的中线．求证：AC=2AE．例4.已知ABC中,AB=AC,A=1000,B的平分线交AC于D,求证:AD+BD=BC.例5.在等边ABC内任取一点P,连PA、PB、PC,求证:以PA、PB、PC为边可以构成一个三角形.例6.已知AD是ABC的角平分线，求证：AD2=AB·AC—BD·DC.2BCDEAABCD情景再现1．ABC中，AB=AC，E为AB上一点，F为AC的延长线上一点，EF交BC于D，DE=DF，求证：BF=CF．2．如图，已知ABC中，ACB=900，ADAB，AD=AB，BEDC，AFAC，求证:CF平分ACB．3.如图,D为等边ABC内一点,DB=DA,BF=AB,DBF=DBC,求BFD的度数.3ABCFEDABDCEF4BCADF