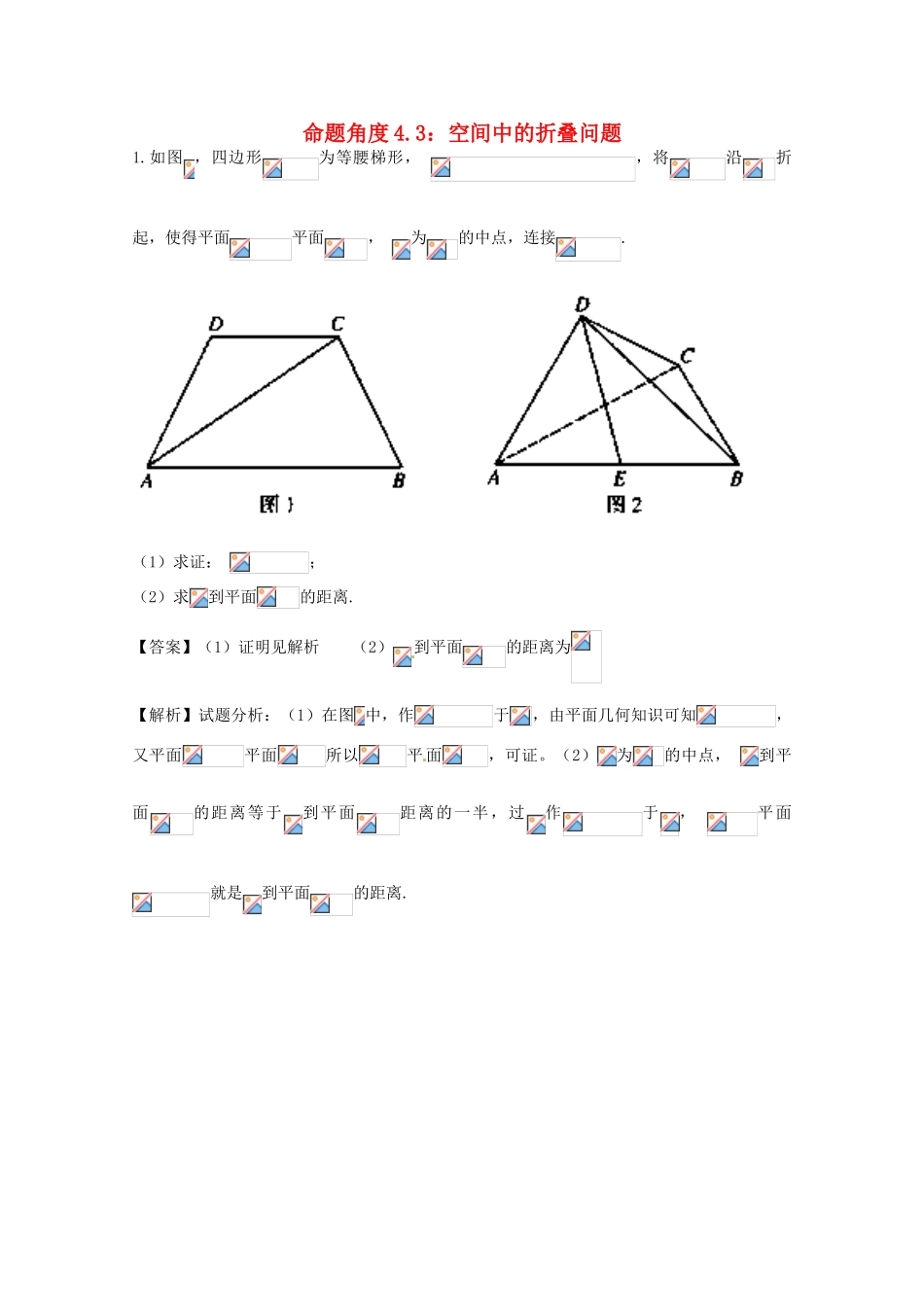
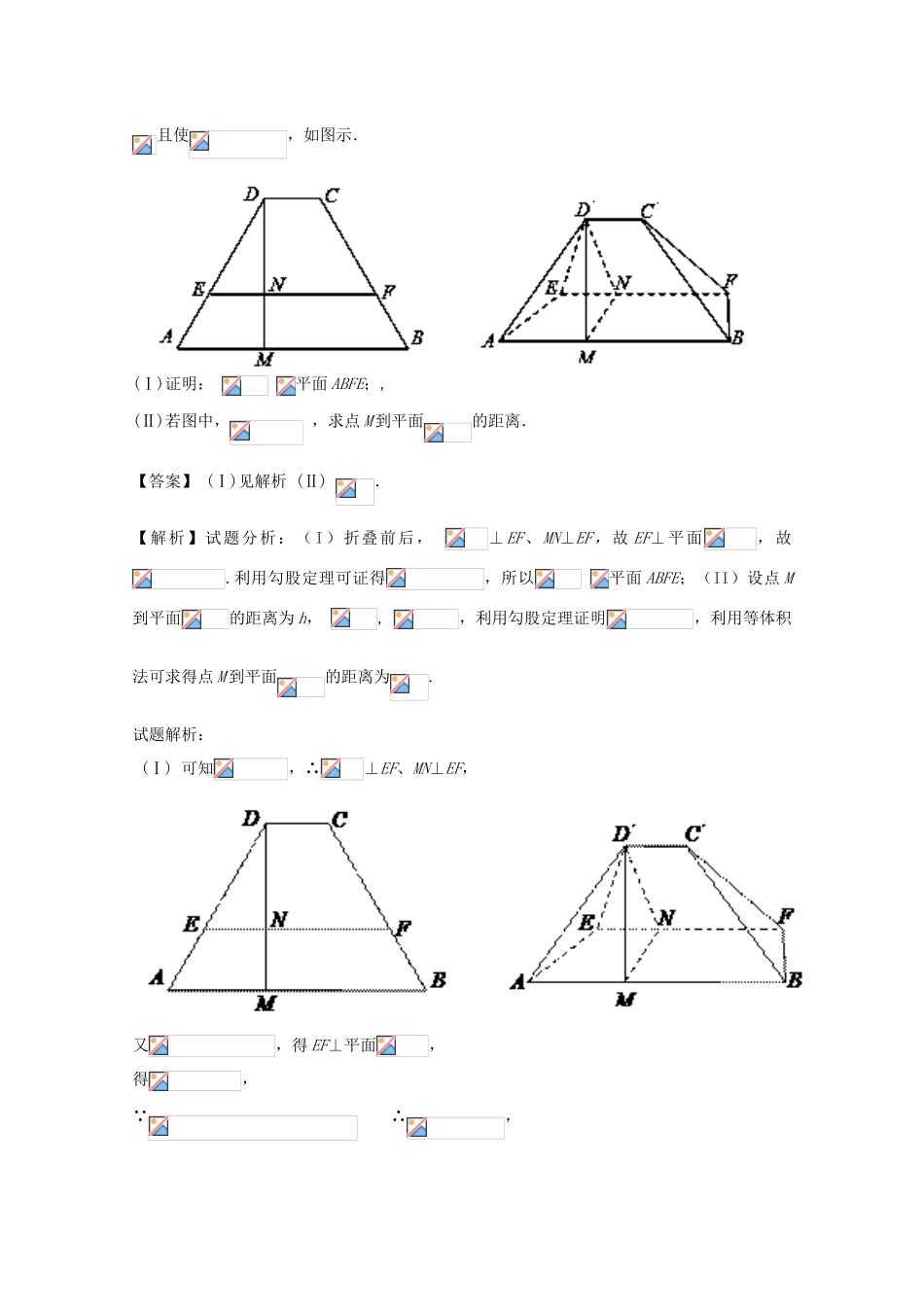
命题角度4.3:空间中的折叠问题1.如图,四边形为等腰梯形,,将沿折起,使得平面平面,为的中点,连接.(1)求证:;(2)求到平面的距离.【答案】(1)证明见解析(2)到平面的距离为【解析】试题分析:(1)在图中,作于,由平面几何知识可知,又平面平面所以平面,可证。(2)为的中点,到平面的距离等于到平面距离的一半,过作于,平面就是到平面的距离.(2)如图,为的中点,到平面的距离等于到平面距离的一半.而平面平面,所以过作于,又由则平面就是到平面的距离.由图易得.到平面的距离为.2.已知下图中,四边形ABCD是等腰梯形,,,于M、交EF于点N,,,现将梯形ABCD沿EF折起,记折起后C、D为、且使,如图示.(Ⅰ)证明:平面ABFE;,(Ⅱ)若图中,,求点M到平面的距离.【答案】(Ⅰ)见解析(Ⅱ).【解析】试题分析:(I)折叠前后,⊥EF、MN⊥EF,故EF⊥平面,故.利用勾股定理可证得,所以平面ABFE;(II)设点M到平面的距离为h,,,利用勾股定理证明,利用等体积法可求得点M到平面的距离为.试题解析:(Ⅰ)可知,∴⊥EF、MN⊥EF,又,得EF⊥平面,得, ∴,又,∴平面ABFE.∴,,又,代入①式,得,解得,∴点M到平面的距离为.3.如图1,在边长为4的正三角形中,分别为的中点,为的中点.将与分别沿同侧折起,使得二面角与二面角的大小都等于90°,得到如图2所示的多面体.(1)在多面体中,求证:四点共同面;(2)求多面体的体积.【答案】(1)见解析(2)【解析】试题分析:(1)由已知条件可证明平面和平面,所以,故四点共同面;(2)利用体积分割求.(2)因为平面,平面,,所以是四棱锥的高,点到平面的距离等于点到平面,又,,,所以.4.以为直径的圆经过、两点,延长、交于点,将沿线段折起,使点在底面的射影恰好为的中点.若,,线段、的中点分别为.(1)判断四点是否共面,并说明理由;(2)求四棱锥的体积.【答案】(1)四点不共面.(2)【解析】试题分析:(1)证明四点不共面,基本方法为反证法,即假设四点共面,则由线线平行得到线面平行平面,再由线面平行得到线线平行,与条件相交矛盾,反设不成立,得到结论,(2)求四棱锥的体积,关键在于求高,而高的寻求往往借助于线面垂直关系得到,本题根据面面垂直性质定理得到线面垂直,,所以为四棱锥的高,再代入体积公式即可.试题解析:(1)假设四点共面,因为,平面,所以平面,又因为平面平面,平面,所以,与已知矛盾,所以四点不共面.(2)由题意,又,于,所以平面所以平面平面,点在底面的射影恰为的中点,所以,所以为四棱锥的高,,∴,,∴∴,,,线段的中点为,所以点到平面的高为连接,所以,,5.如图(1),五边形中,.如图(2),将沿折到的位置,得到四棱锥.点为线段的中点,且平面.(1)求证:平面平面;(2)若直线与所成角的正切值为,设,求四棱锥的体积.【答案】(1)见解析;(2).【解析】试题分析:(1)要证明面面垂直,一般先证线面垂直,题中已知平面,由于是的中点,只要取的中点,可证,从而得平面,因此就得到面面垂直;(2)由(1)的垂直可证是等边三角形,因此有,再得,于是有平面,可得,这样可求得图形中各线段长,可得四棱锥的底面积和高,得体积.试题解析:(1)证明:取的中点,连接,则,又,所以,则四边形为平行四边形,所以,又平面,∴平面,∴平面平面PCD;所以所以.,∴为直线与所成的角,由(1)可得,∴,∴,由,可知,则.6.如图(1)所示,已知四边形是由直角△和直角梯形拼接而成的,其中.且点为线段的中点,,现将△沿进行翻折,使得二面角的大小为,得到图形如图(2)所示,连接,点分别在线段上.(1)证明:;(2)若三棱锥的体积为四棱锥体积的,求点到平面的距离.【答案】(1)见解析(2)【解析】试题分析:(1)利用线面垂直的判断定理可证得平面,则.(2)利用体积的比值结合体积公式可得点到平面的距离为.试题解析:(Ⅰ)因为平面平面,又,所以平面.又平面,所以.在直角梯形中,,,,所以,又,所以,即,又,所以平面.因为平面,所以.(Ⅱ)设点到平面的距离为,因为,且,所,即,故点到平面的距离为.7.如图,在矩形中,分别为的中点,现将沿折起,得四棱...