高考数学复习点拨 巧用线性规划思想解题VIP免费

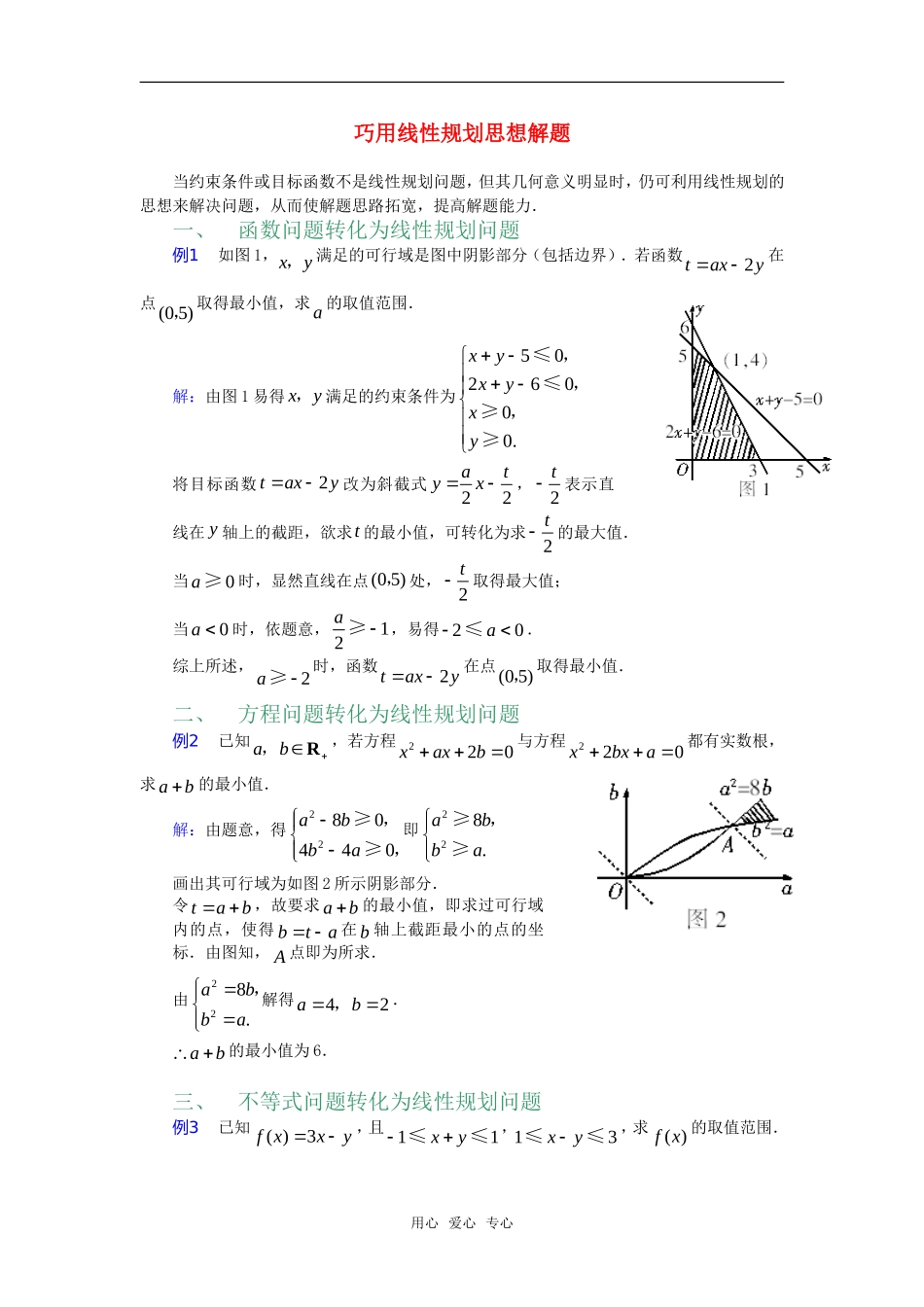
巧用线性规划思想解题当约束条件或目标函数不是线性规划问题，但其几何意义明显时，仍可利用线性规划的思想来解决问题，从而使解题思路拓宽，提高解题能力．一、函数问题转化为线性规划问题例1如图1，xy，满足的可行域是图中阴影部分（包括边界）．若函数2taxy在点(05)，取得最小值，求a的取值范围．解：由图1易得xy，满足的约束条件为5026000.xyxyxy，，，≤≤≥≥将目标函数2taxy改为斜截式22atyx，2t表示直线在y轴上的截距，欲求t的最小值，可转化为求2t的最大值．当0a≥时，显然直线在点(05)，处，2t取得最大值；当0a时，依题意，12a≥，易得20a≤．综上所述，2a≥时，函数2taxy在点(05)，取得最小值．二、方程问题转化为线性规划问题例2已知abR，，若方程220xaxb与方程220xbxa都有实数根，求ab的最小值．解：由题意，得2280440abba，，≥≥即228.abba，≥≥画出其可行域为如图2所示阴影部分．令tab，故要求ab的最小值，即求过可行域内的点，使得bta在b轴上截距最小的点的坐标．由图知，A点即为所求．由228.abba，解得42ab，．ab的最小值为6．三、不等式问题转化为线性规划问题例3已知()3fxxy，且11xy≤≤，13xy≤≤，求()fx的取值范围．用心爱心专心解：如图3，作出不等式组1113xyxy，，≤≤≤≤所表示的平面区域，即可行域．作直线:30lxy，把直线l向右下方平移过(01)B，，即直线10xy与10xy的交点时，min()3011fx；再把直线l向右下方平移过(21)A，即直线30xy与10xy的交点时，max()2317fx，1()7fx≤≤．说明：本题还可运用整体代换法，先用xy与xy的一次组合表示，找出它们之间的线性关系，然后利用不等式的性质加以解决．四、多元问题转化为线性规划问题例4已知ABC△的三边长abc，，满足2bca≤，2acb≤，求ba的取值范围．解：由题意，应用22000abcabacbcababc，，，，，，≤≤令bcxyaa，，上述不等式可化为1212100.xyxyxyxxy，，，，≤≤求出x的范围即可．作出可行域如图4，易得2332x，于是ba的范围为2332，．用心爱心专心