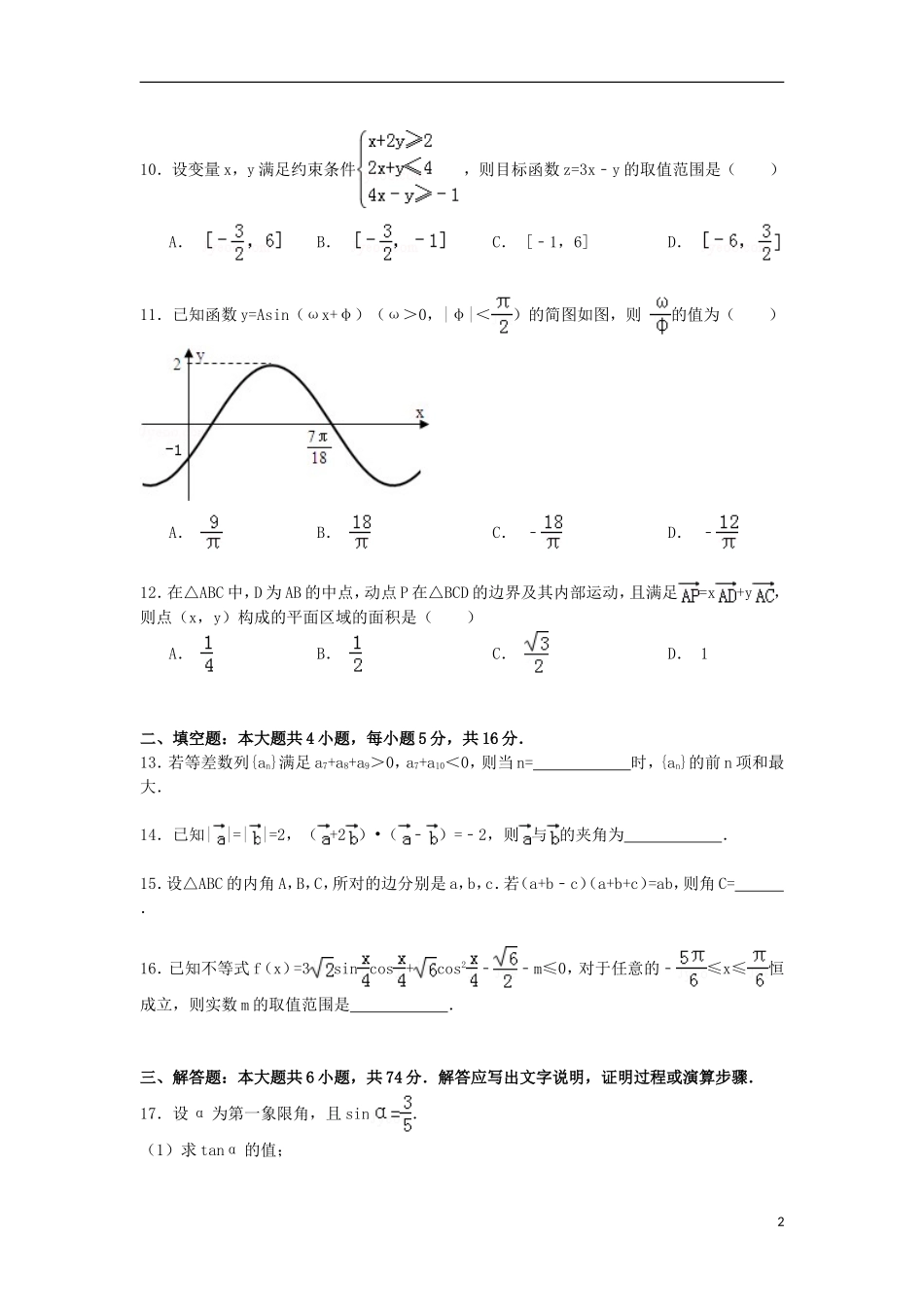
2014-2015学年辽宁省葫芦岛市高一(下)期末数学试卷(文科)一、选择题:本大题共12小题,每小题5分,共60分,在每小题给出的四个选项中,只有一个是符合题目要求的.1.sin的值是()A.B.C.D.2.若向量,向量,则=()A.(﹣2,﹣4)B.(3,4)C.(6,10)D.(﹣6,﹣10)3.等差数列{an}的前n项和为Sn,若a2=3,S5=25,则a6等于()A.7B.9C.11D.134.如果a<b<0,那么下列不等式成立的是()A.B.ab<b2C.﹣ab<﹣a2D.5.已知{an}为等比数列,a5+a8=2,a6•a7=﹣8,则a2+a11=()A.5B.7C.﹣7D.﹣56.设x,y为正数,则(x+y)(+)的最小值为()A.6B.9C.12D.157.△ABC的三个内角A、B、C所对的边分别为a,b,c,asinAsinB+bcos2A=a,则=()A.2B.2C.D.8.已知向量=(k,3),,=(1,﹣3),且(2),则实数k=()A.﹣B.0C.3D.9.已知等比数列{an}的各项均为正数,且a2015=a2014+2a2013,若数列中存在两项am,an,使得=4a1,则的最小值为()A.B.C.D.不存在110.设变量x,y满足约束条件,则目标函数z=3x﹣y的取值范围是()A.B.C.[﹣1,6]D.11.已知函数y=Asin(ωx+φ)(ω>0,|φ|<)的简图如图,则的值为()A.B.C.﹣D.﹣12.在△ABC中,D为AB的中点,动点P在△BCD的边界及其内部运动,且满足=x+y,则点(x,y)构成的平面区域的面积是()A.B.C.D.1二、填空题:本大题共4小题,每小题5分,共16分.13.若等差数列{an}满足a7+a8+a9>0,a7+a10<0,则当n=时,{an}的前n项和最大.14.已知||=||=2,(+2)•(﹣)=﹣2,则与的夹角为.15.设△ABC的内角A,B,C,所对的边分别是a,b,c.若(a+b﹣c)(a+b+c)=ab,则角C=.16.已知不等式f(x)=3sincos+cos2﹣﹣m≤0,对于任意的﹣≤x≤恒成立,则实数m的取值范围是.三、解答题:本大题共6小题,共74分.解答应写出文字说明,证明过程或演算步骤.17.设α为第一象限角,且sin.(1)求tanα的值;2(2)求的值.18.已知数列{an}为等比数列,且a2=2,a5=16.(1)求数列{an}的通项公式;(2)记bn=an•log2an+1,数列{bn}的前n项和为Tn,求Tn.19.已知函数f(x)=4sin2(+x)﹣2.(1)求f(x)的单调递增区间;(2)若不等式|f(x)﹣m|<2在时恒成立,求实数m的取值范围.20.已知a,b,c分别为△ABC三个内角A,B,C的对边,(1)求A;(2)若a=2,△ABC的面积为,求b,c.21.已知数列{an}为等差数列,a3=5,a4+a8=22.(1)求数列{an}的通项公式an及前n项和公式Sn;(2)令bn=,求证:b1+b2+…bn<.22.已知向量=(﹣2,1),=(1,2),若存在非零实数m,n使得+(n+1),+(n+4),且,试求的取值范围.32014-2015学年辽宁省葫芦岛市高一(下)期末数学试卷(文科)参考答案与试题解析一、选择题:本大题共12小题,每小题5分,共60分,在每小题给出的四个选项中,只有一个是符合题目要求的.1.sin的值是()A.B.C.D.考点:运用诱导公式化简求值.专题:计算题.分析:利用诱导公式sin(π﹣α)=sinα即可.解答:解: sin=sin(π﹣)=sin=,故选C.点评:本题考查运用诱导公式化简求值,属于基础题.2.若向量,向量,则=()A.(﹣2,﹣4)B.(3,4)C.(6,10)D.(﹣6,﹣10)考点:平面向量的坐标运算.专题:平面向量及应用.分析:由向量,向量,知,再由,能求出结果.解答:解: 向量,向量,∴,∴=(﹣4,﹣7)﹣(﹣2,﹣3)=(﹣2,﹣4).故选A.点评:本题考查平面向量的坐标运算,是基础题.解题时要认真解答,仔细运算.3.等差数列{an}的前n项和为Sn,若a2=3,S5=25,则a6等于()A.7B.9C.11D.13考点:等差数列的前n项和.4专题:等差数列与等比数列.分析:根据等差数列的通项公式和前n项和公式求出首项和公差即可.解答:解: a2=3,S5=25,∴,即,解得a1=1,d=2,则a6=a1+5d=1+5×2=11,故选:C点评:本题主要考查等差数列项的求解,根据条件求出数列的首项和公差是解决本题的关键.4.如果a<b<0,那么下列不等式成立的是()A.B.ab<b2C.﹣ab<﹣a2D.考点:不等关系与不等式.专题:不等式的解法及应用.分析...