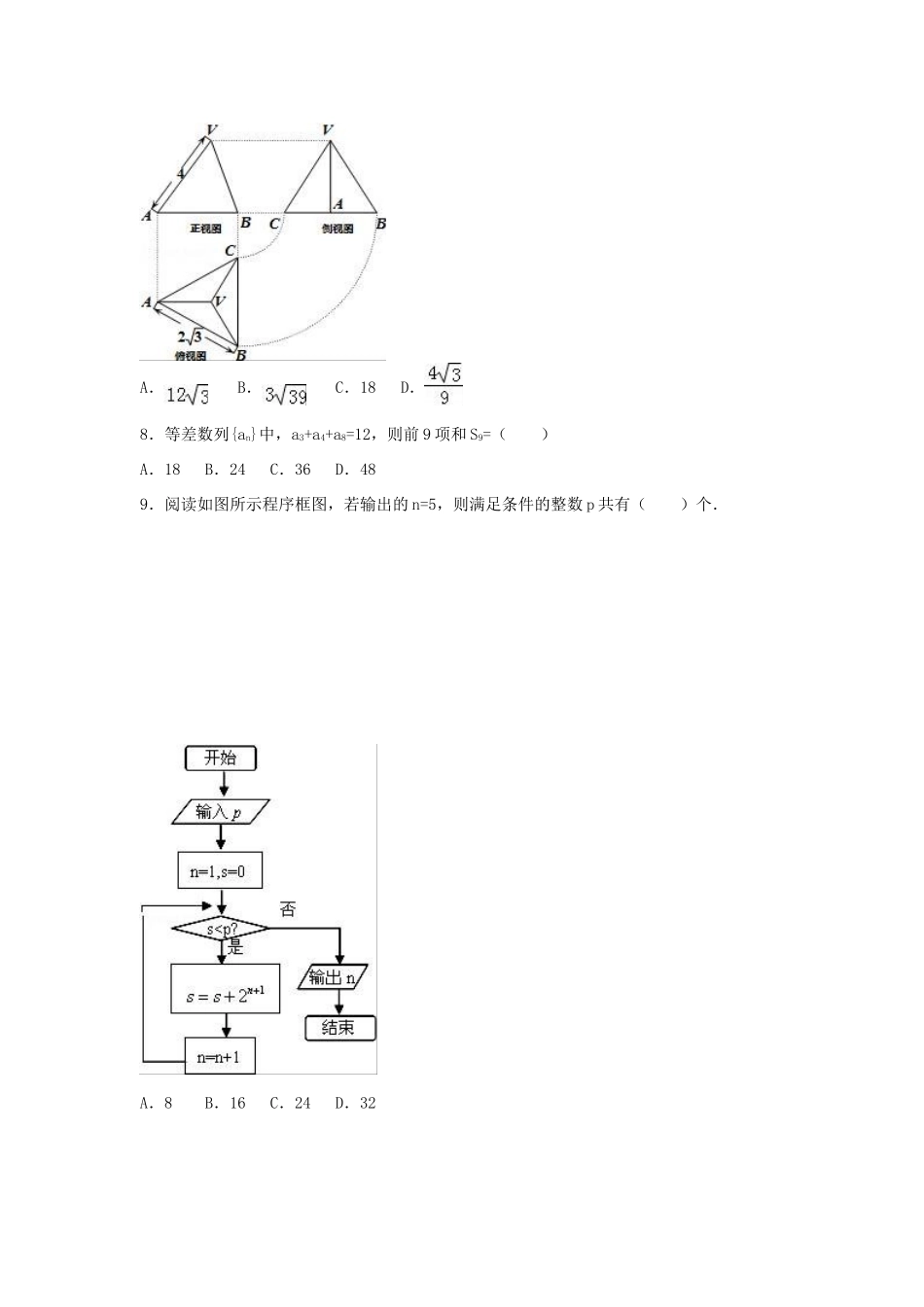
2016年辽宁省沈阳市高考数学三模试卷(文科)一.选择题:(本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的)1.复数()3的模是()A.B.C.1D.22.已知集合A={x|(x﹣1)(x﹣2)(x﹣3)=0},集合B=,则集合A∩B真子集的个数是()A.1B.2C.3D.43.若直线l:x+y+a=0被圆x2+y2=a截得的弦长为,则a的值为()A.﹣1B.C.1D.24.已知函数f(x)是定义在R上的偶函数,若当x<0时,f(x)=﹣log2(﹣2x),则f(32)=()A.﹣32B.﹣6C.6D.645.抛物线y2=2px(p>0)上的动点Q到其焦点的距离的最小值为1,则p=()A.B.1C.2D.46.已知θ∈(﹣,)且sinθ+cosθ=a,其中a∈(0,1),则tanθ的可能取值是()A.﹣3B.3或C.D.﹣3或7.已知正三棱锥V﹣ABC的正视图、侧视图和俯视图如图所示,则该正三棱锥侧面积是()A.B.C.18D.8.等差数列{an}中,a3+a4+a8=12,则前9项和S9=()A.18B.24C.36D.489.阅读如图所示程序框图,若输出的n=5,则满足条件的整数p共有()个.A.8B.16C.24D.3210.设x、y满足约束条件若目标函数z=ax+by(a>0,b>0)的最大值为12,则a2+b2的最小值为()A.B.C.D.11.设F为双曲线的左焦点,在x轴上F点的右侧有一点A,以FA为直径的圆与双曲线左、右两支在x轴上方的交点分别为M,N,则的值为()A.B.C.D.12.关于x的方程2ax=x2﹣2alnx有唯一解,则正实数a的值为()A.B.1C.D.2二.填空题:(本大题共4小题,每小题5分,共20分,把答案填在答题卡的相应位置上)13.已知等比数列{an}的公比q=2,其前4项和S4=60,则a2=.14.已知向量,的夹角为,=(﹣1,1),||=2,则|+2|=.15.在区间[0,3]上随机地取一个数x,则事件“﹣1≤log(x+)≤1”发生的概率为.16.已知球O的半径为1,点A,B,C是球大圆上的任意三点,点P是球面上的任意一点,则三棱锥P﹣ABC的最大体积为.三.解答题:(本大题共5小题,共70分,解答应写出文字说明、证明过程或演算步骤)17.已知在△ABC中,角A、B、C的对边分别为a、b、c,若cosA=,a=2,3sinC=4sinB.(Ⅰ)求b,c的值;(Ⅱ)若等差数列{an}中a1=a,a2=b.(ⅰ)求数列{an}的通项公式;(ⅱ)设bn=(﹣1)nan,求数列{bn}的前n项和Tn.18.如图,四棱锥P﹣ABCD的底面是直角梯形,AD∥BC,∠ADC=90°,AD=2BC,PA⊥平面ABCD,E为线段PA的中点.(Ⅰ)求证:BE∥平面PCD;(Ⅱ)若PA=AD=2,求点E到平面PCD的距离.19.襄阳市某优质高中为了选拔学生参加“全国中学生英语能力竞赛(NEPCS)”,先在本校进行初赛(满分150分),若该校有100名学生参加初赛,并根据初赛成绩得到如图所示的频率分布直方图.(1)根据频率分布直方图,计算这100名学生参加初赛成绩的中位数;(2)该校推荐初赛成绩在110分以上的学生代表学校参加竞赛,为了了解情况,在该校推荐参加竞赛的学生中随机抽取2人,求选取的两人的初赛成绩在频率分布直方图中处于不同组的概率.20.设P为椭圆=1(a>b>0)上任一点,F1,F2为椭圆的焦点,|PF1|+|PF2|=4,离心率为.(Ⅰ)求椭圆的标准方程;(Ⅱ)直线l:y=kx+m(m≠0)经过点(﹣1,0),且与椭圆交于P、Q两点,若直线OP,PQ,OQ的斜率依次成等比数列,求直线l的方程.21.已知函数f(x)=exsinx,其中x∈R,e=2.71828…为自然对数的底数.(Ⅰ)求函数f(x)的单调区间;(Ⅱ)当时,f(x)≥kx,求实数k的取值范围.四.请考生在22,23,24三题中任选一题作答,如果多做,则按所做的第一题记分.作答时,用2B铅笔在答题卡上把所选题目对应的标号涂黑.[选修4-1:几何证明选讲]22.如图,△ABC是直角三角形,∠ABC=90°,以AB为直径的圆O交AC于N,过N作圆O的切线交BC于D,OD交圆O于点M.(Ⅰ)证明:OD∥AC;(Ⅱ)证明:+1.[选修4-4:坐标系与参数方程]23.在平面直角坐标系中,过点P(3,1)的直线l的参数方程为(t为参数,α为l的倾斜角).以坐标原点为极点,x轴的正半轴为极轴,建立极坐标系.曲线C1:ρ=2cosθ,曲线C2:ρ=4cosθ.(Ⅰ)若直线l与曲线C1有且仅有一个公共点,求直线l的极坐标方程;(Ⅱ)若直线l与曲...