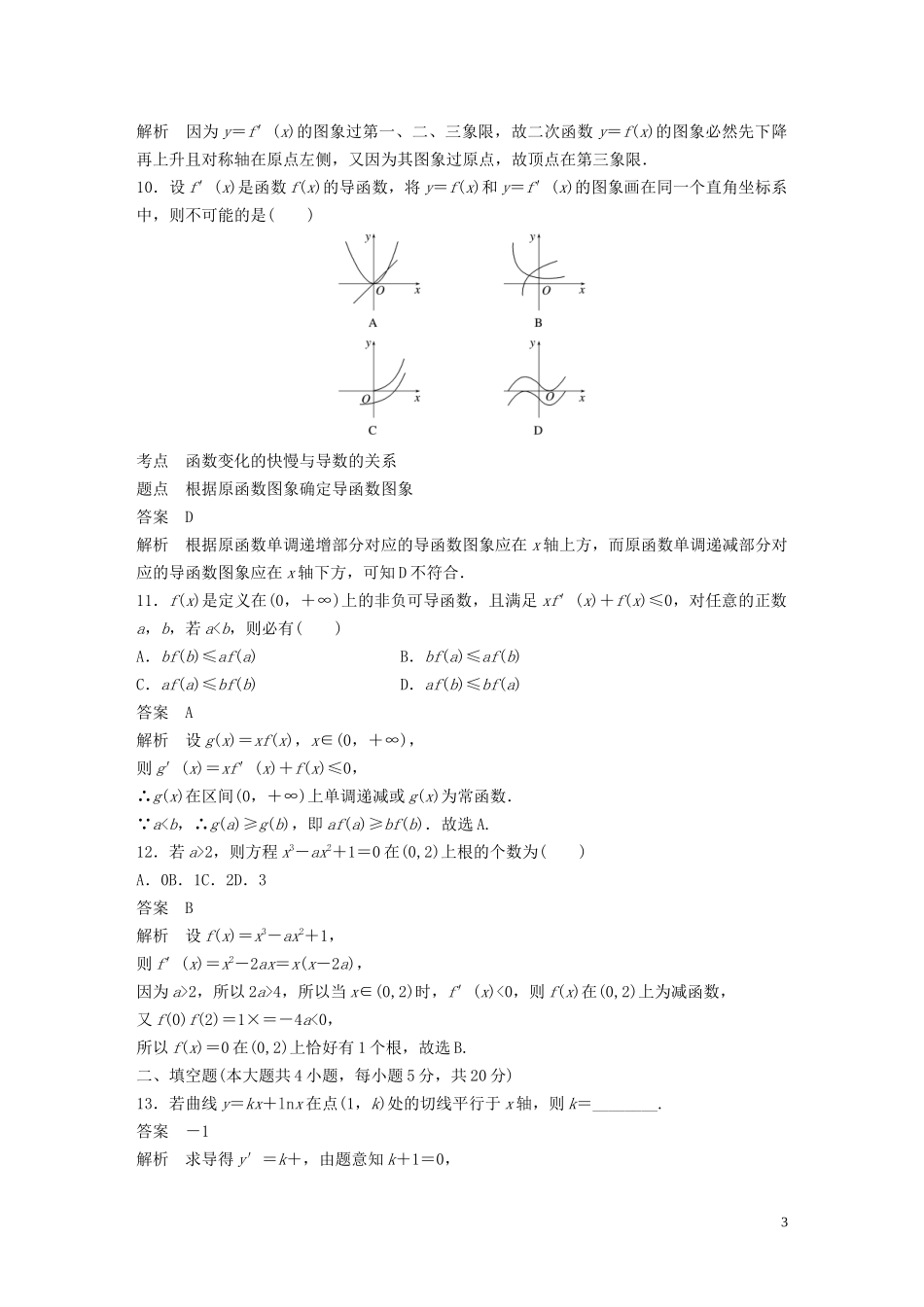
章末检测试卷(三)(时间:120分钟满分:150分)一、选择题(本大题共12小题,每小题5分,共60分)1.下列导数运算正确的是()A.′=1+B.(2x)′=x2x-1C.(cosx)′=sinxD.(xlnx)′=lnx+1答案D解析根据导数的运算公式可得′=1-,故A错误;(2x)′=2xln2,故B错误;(cosx)′=-sinx,故C错误;(xlnx)′=lnx+1,故D正确.2.f(x)=ax3+3x2+2,若f′(-1)=4,则a的值为()A.B.C.D.答案D解析f′(x)=3ax2+6x,f′(-1)=3a-6=4,a=.3.已知函数f(x)=x2+f′(2)(lnx-x),则f′(1)等于()A.1B.2C.3D.4答案B解析 f′(x)=2x+f′(2),∴f′(2)=,∴f′(x)=2x+,∴f′(1)=2.4.若函数y=a(x3-x)的单调递增区间是,,则a的取值范围是()A.a>0B.-1
1D.00的解集为,,∴a>0.5.如图所示,y=f(x)是可导函数,直线l:y=kx+3是曲线y=f(x)在x=1处的切线,令h(x)=xf(x),h′(x)是h(x)的导函数,则h′(1)的值是()A.2B.1C.-1D.答案B解析由题图可知曲线的切线经过点(1,2),1则k+3=2,得k=-1,即f′(1)=-1,且f(1)=2. h(x)=xf(x),∴h′(x)=f(x)+xf′(x),则h′(1)=f(1)+f′(1)=2-1=1,故选B.6.对于实数集R上的可导函数f(x),若满足(x2-3x+2)·f′(x)<0,则当x∈[1,2]时必有()A.f(1)≤f(x)≤f(2)B.f(x)≤f(1)C.f(x)≥f(2)D.f(x)≤f(1)或f(x)≥f(2)答案A解析因为(x2-3x+2)f′(x)<0,所以或故当x∈[1,2]时,f(x)为增函数,有f(1)≤f(x)≤f(2).7.已知a,b为正实数,函数f(x)=ax3+bx+2x在[0,1]上的最大值为4,则f(x)在[-1,0]上的最小值为()A.-B.C.-2D.2答案A解析 f′(x)=3ax2+b+2xln2>0,∴f(x)在[0,1],[-1,0]上都为增函数,当x∈[0,1]时,f(x)max=f(1)=a+b+2=4,∴a+b=2,当x∈[-1,0]时,f(x)min=f(-1)=-(a+b)+2-1=-2+=-.8.设f(x)=xlnx,若f′(x0)=2,则x0等于()A.e2B.ln2C.D.e答案D解析 f′(x)=x′·lnx+x·(lnx)′=1+lnx,∴f′(x0)=1+lnx0=2,∴lnx0=1,∴x0=e.9.二次函数y=f(x)的图象过原点,且它的导函数y=f′(x)的图象过第一、二、三象限的一条直线,则函数y=f(x)的图象的顶点在()A.第一象限B.第二象限C.第三象限D.第四象限答案C2解析因为y=f′(x)的图象过第一、二、三象限,故二次函数y=f(x)的图象必然先下降再上升且对称轴在原点左侧,又因为其图象过原点,故顶点在第三象限.10.设f′(x)是函数f(x)的导函数,将y=f(x)和y=f′(x)的图象画在同一个直角坐标系中,则不可能的是()考点函数变化的快慢与导数的关系题点根据原函数图象确定导函数图象答案D解析根据原函数单调递增部分对应的导函数图象应在x轴上方,而原函数单调递减部分对应的导函数图象应在x轴下方,可知D不符合.11.f(x)是定义在(0,+∞)上的非负可导函数,且满足xf′(x)+f(x)≤0,对任意的正数a,b,若a2,则方程x3-ax2+1=0在(0,2)上根的个数为()A.0B.1C.2D.3答案B解析设f(x)=x3-ax2+1,则f′(x)=x2-2ax=x(x-2a),因为a>2,所以2a>4,所以当x∈(0,2)时,f′(x)<0,则f(x)在(0,2)上为减函数,又f(0)f(2)=1×=-4a<0,所以f(x)=0在(0,2)上恰好有1个根,故选B.二、填空题(本大题共4小题,每小题5分,共20分)13.若曲线y=kx+lnx在点(1,k)处的切线平行于x轴,则k=________.答案-1解析求导得y′=k+,由题意知k+1=0,3所以k=-1.14.已知函数f(x)=-x3+ax在区间(-1,1)上是增函数,则实数a的取值范围是________.答案{a|a≥3}解析由题意知f′(x)=-3x2+a≥0在区间(-1,1)上恒成立,则a≥3x2,x∈(-1,1)恒成立,故a≥3.15.若函数f(x)=x3+ax2-2x+5在区间上既不是单调递增函数,也不是单调递减函数,则实数a的取值范围是________.答案解析因为f′(x)=3x2+2ax-2...