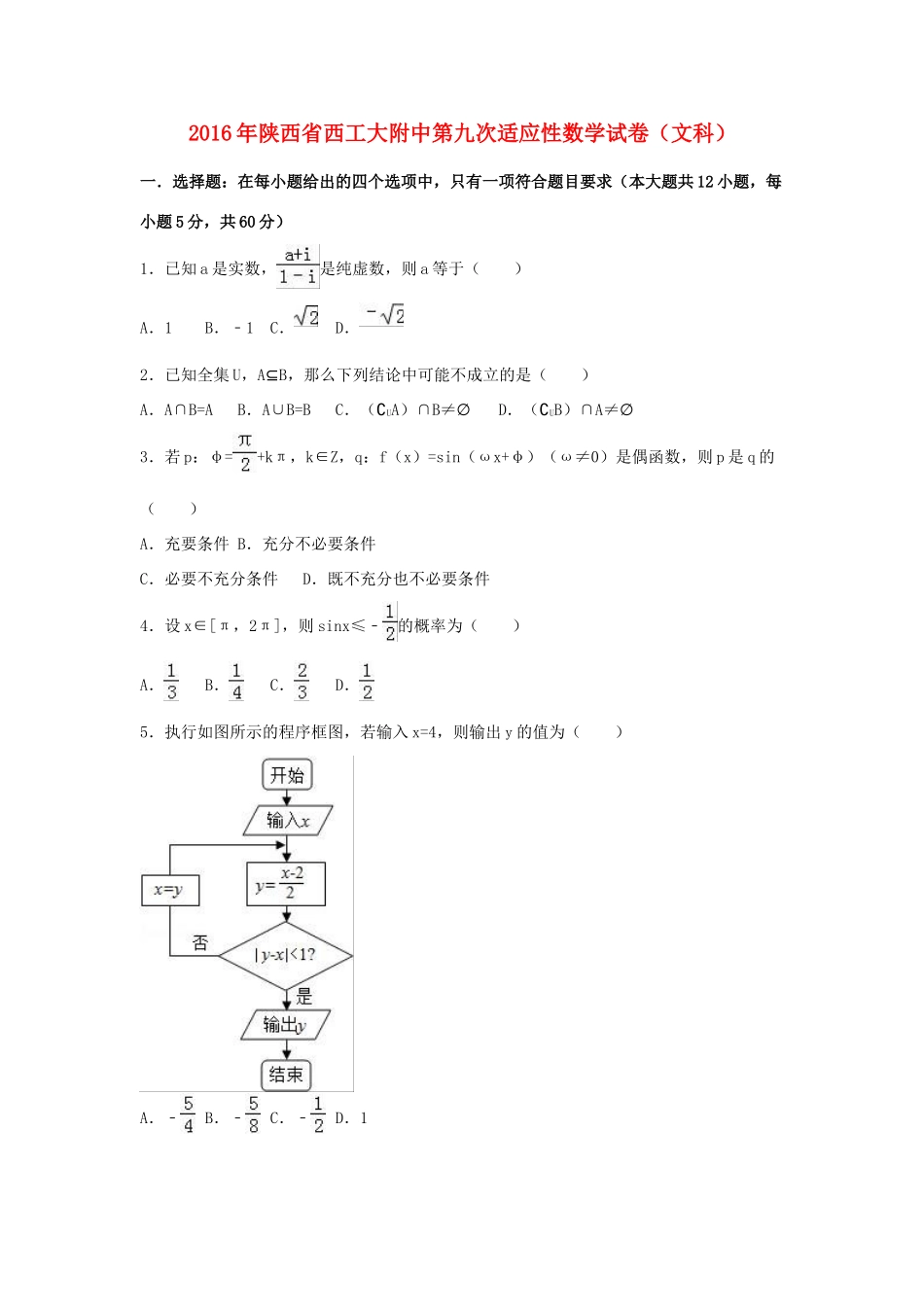
2016年陕西省西工大附中第九次适应性数学试卷(文科)一.选择题:在每小题给出的四个选项中,只有一项符合题目要求(本大题共12小题,每小题5分,共60分)1.已知a是实数,是纯虚数,则a等于()A.1B.﹣1C.D.2.已知全集U,A⊆B,那么下列结论中可能不成立的是()A.A∩B=AB.A∪B=BC.(∁UA)∩B≠∅D.(∁UB)∩A≠∅3.若p:φ=+kπ,k∈Z,q:f(x)=sin(ωx+φ)(ω≠0)是偶函数,则p是q的()A.充要条件B.充分不必要条件C.必要不充分条件D.既不充分也不必要条件4.设x∈[π,2π],则sinx≤﹣的概率为()A.B.C.D.5.执行如图所示的程序框图,若输入x=4,则输出y的值为()A.﹣B.﹣C.﹣D.16.若非零向量,满足||=||=|+|,则与﹣夹角为()A.B.C.D.7.设x,y满足约束条件,则目标函数z=4x+y的最小值为()A.﹣1B.0C.1D.28.已知数列{an}的通项公式为an=log2(n∈N*),设其前n项和为Sn,则使Sn<﹣5成立的自然数n()A.有最小值63B.有最大值63C.有最小值31D.有最大值319.某商场中秋前30天月饼销售总量f(t)与时间t(0<t≤30)的关系大致满足f(t)=t2+10t+16,则该商场前t天平均售出(如前10天的平均售出为)的月饼最少为()A.18B.27C.20D.1610.直线ax+by=1与圆x2+y2=1相交于A,B两点(其中a,b是实数),且△AOB是直角三角形(O是坐标原点),则点P(a,b)与点(0,1)之间距离的最大值为()A.+1B.2C.D.﹣111.若0<x<,0<y<,且sinx=xcosy,则()A.B.C.D.x<y12.给出下列命题:①在区间(0,+∞)上,函数y=x﹣1,,y=(x﹣1)2,y=x3中有三个是增函数;②若logm3<logn3<0,则0<n<m<1;③若函数f(x)是奇函数,则f(x﹣1)的图象关于点A(1,0)对称;④已知函数则方程有2个实数根,其中正确命题的个数为()A.1B.2C.3D.4二.填空题:把答案填写在答题卡相应的题号后的横线上(本大题共4小题,每小题5分,共20分)13.某校开展“向感动中国2015年度人物学习”主题墙报评比,9位评委为A班的墙报,给出的分数如茎叶图所示.记分员在去掉一个最高分和一个最低分后,算得平均分为91,复核员在复核时,发现有一个数字(茎叶图中的x)无法看清,若记分员计算无误,则数字x应该是.14.椭圆C的两个焦点分别为F1(﹣1,0)和F2(1,0),若该椭圆C与直线x+y﹣3=0有公共点,则其离心率的最大值为.15.某几何体的三视图如图所示,则该几何体的体积为.16.观察下列式子:根据以上式子可以猜想:1+<(n≥2).三.解答题:解答应写出文字说明、证明过程或演算步骤(本大题共5小题,共70分).17.已知向量,(1)当∥时,求2cos2x﹣sin2x的值;(2)求在上的值域.18.某高校共有15000人,其中男生10500人,女生4500人,为调查该校学生每周平均体育运动时间的情况,采用分层抽样的方法,收集300位学生每周平均体育运动时间的样本数据(单位:小时)(Ⅰ)应收集多少位女生样本数据?(Ⅱ)根据这300个样本数据,得到学生每周平均体育运动时间的频率分布直方图(如图所示),其中样本数据分组区间为:[0,2],(2,4],(4,6],(6,8],(8,10],(10,12]估计该校学生每周平均体育运动时间超过4个小时的概率.(Ⅲ)在样本数据中,有60位女生的每周平均体育运动时间超过4个小时.请完成每周平均体育运动时间与性别的列联表,并判断是否有95%的把握认为“该校学生的每周平均体育运动时间与性别有关”.附:P(K2≥k0)0.100.050.0100.005k02.7063.8416.6357.87919.如图,PA⊥平面ABCD,四边形ABCD是矩形,PA=AB=1,点F是PB的中点,点E在边BC上移动.(Ⅰ)点E为BC的中点时,试判断EF与平面PAC的位置关系,并说明理由;(Ⅱ)证明:无论点E在边BC的何处,都有PE⊥AF.20.已知椭圆C:(a>b>0)的离心率为e=,以原点为圆心,椭圆短半轴长为半径的圆与直线x﹣y=0相切.(Ⅰ)求椭圆C的标准方程;(Ⅱ)设F1(﹣1,0),F2(1,0),若过F1的直线交曲线C于A、B两点,求•的取值范围.21.已知函数f(x)的导函数f′(x)=x2+2ax+b(ab≠0),且f(0)=0.设曲线y=f(x)在原点处的切线l1的斜率为k1,过原点的...