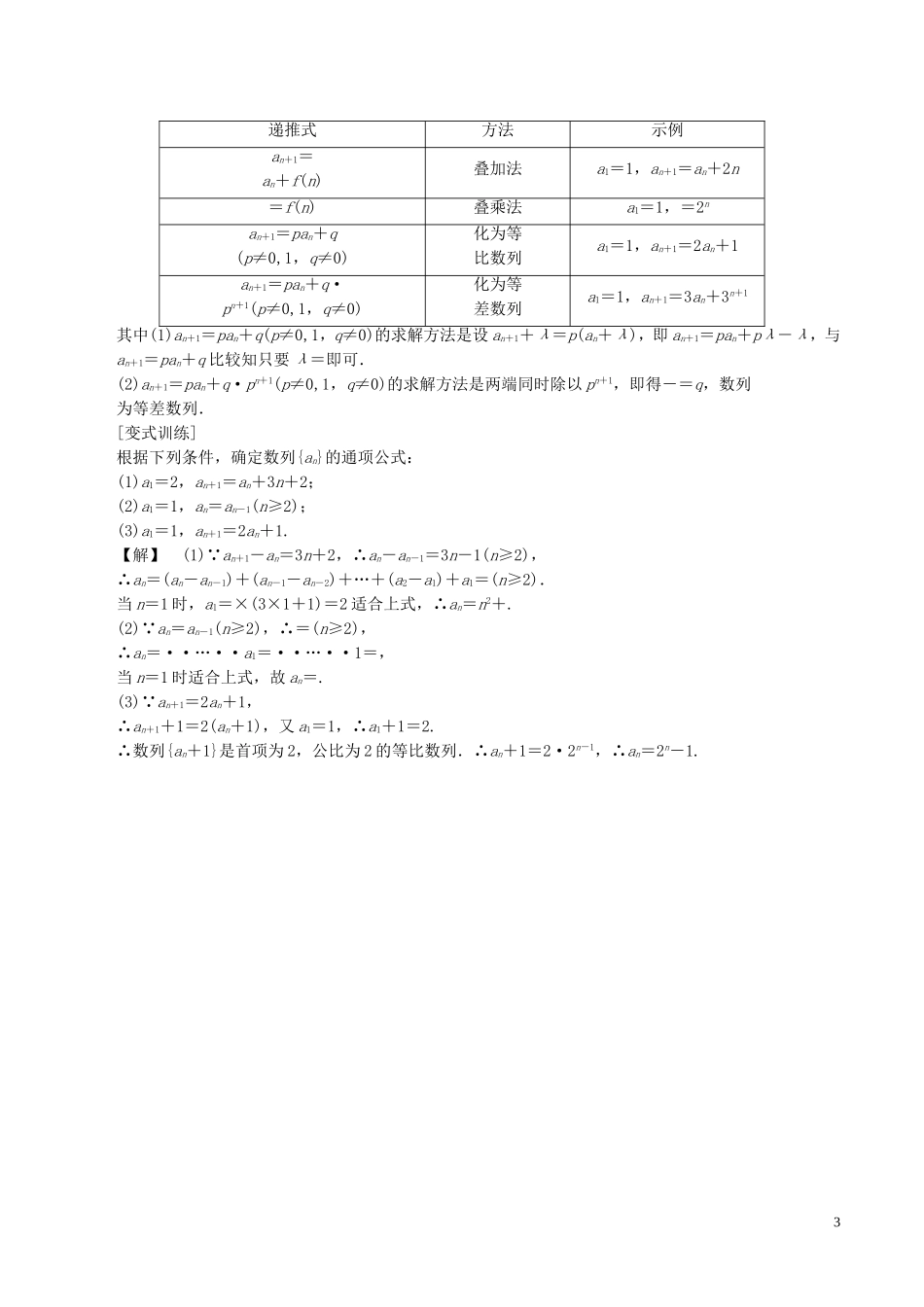
数列的概念与简单表示法考向1由数列的前几项归纳数列的通项公式1.(2016·太原模拟)数列1,3,6,10,…的一个通项公式是()A.an=n2-(n-1)B.an=n2-1C.an=D.an=【解析】观察数列1,3,6,10,…可以发现1=1,3=1+2,6=1+2+3,10=1+2+3+4,…第n项为1+2+3+4+…+n=.∴an=.【答案】C2.数列{an}的前4项是,1,,,则这个数列的一个通项公式是an=________.【解析】数列可以看作,,,,…,分母可以看作12+1,22+1,32+1,42+1,第n项分母为n2+1,分子可以看作2×1+1,2×2+1,2×3+1,2×4+1,第n项分子为2n+1,故an=.【答案】由前几项归纳数列通项的常用方法及具体策略1.常用方法:观察(观察规律)、比较(比较已知数列)、归纳、转化(转化为特殊数列)、联想(联想常见的数列)等方法.2.具体策略:(1)分式中分子、分母的特征;(2)相邻项的变化特征;(3)拆项后的特征;(4)各项的符号特征和绝对值特征;(5)化异为同,对于分式还可以考虑对分子、分母各个击破,或寻找分子、分母之间的关系;(6)对于符号交替出现的情况,可用(-1)k或(-1)k+1,k∈N*处理.考向2由an与Sn的关系求通项(1)若数列{an}的前n项和Sn=an+,则{an}的通项公式an=________.(2)已知下面数列{an}的前n项和Sn,求{an}的通项公式:①Sn=2n2-3n;②Sn=3n+b.【解析】(1)由Sn=an+得,当n≥2时,Sn-1=an-1+,两式相减,整理得an=-2an-1,又n=1时,S1=a1=a1+,∴a1=1,∴{an}是首项为1,公比为-2的等比数列,故an=(-2)n-1.【答案】(-2)n-1(2)①a1=S1=2-3=-1,当n≥2时,an=Sn-Sn-1=(2n2-3n)-[2(n-1)2-3(n-1)]=4n-5,由于a1也适合此等式,∴an=4n-5.②a1=S1=3+b,当n≥2时,an=Sn-Sn-1=(3n+b)-(3n-1+b)=2·3n-1.当b=-1时,a1适合此等式.当b≠-1时,a1不适合此等式.1∴当b=-1时,an=2·3n-1;当b≠-1时,an=已知Sn求an的三个步骤1.当n=1时,a1=S1.2.当n≥2时,an=Sn-Sn-1.3.对n=1时的结果进行检验,看是否符合n≥2时an的表达式,如果符合,则可以把数列的通项公式合写;如果不符合,则an应写成分段函数的形式,即an=[变式训练]1.设数列{an}的前n项和Sn=n2,则a8的值为()A.15B.16C.49D.64【解析】a8=S8-S7=82-72=15.【答案】A2.已知数列{an}的前n项和为Sn,a1=1,Sn=2an+1,则Sn=()A.2n-1B.n-1C.n-1D.【解析】由an+1=Sn+1-Sn,得Sn=Sn+1-Sn,即Sn+1=Sn(n≥1),又S1=a1=1,所以数列{Sn}是首项为1,公比为的等比数列,所以Sn=n-1,故选B.【答案】B考向3由数列的递推公式求通项公式1.根据下列条件,确定数列{an}的通项公式:(1)a1=2,an+1=an+ln;(2)a1=1,an+1=2nan;(3)a1=1,an+1=3an+2.【解】(1)∵an+1=an+ln,∴an-an-1=ln=ln(n≥2),∴an=(an-an-1)+(an-1-an-2)+…+(a2-a1)+a1=ln+ln+…+ln+ln2+2=2+ln=2+lnn(n≥2).又a1=2适合上式,故an=2+lnn(n∈N*).(2)∵an+1=2nan,∴=2n-1(n≥2),∴an=··…··a1=2n-1·2n-2·…·2·1=21+2+3+…+(n-1)=2.又a1=1适合上式,故an=2.(3)∵an+1=3an+2,∴an+1+1=3(an+1),又a1=1,∴a1+1=2,故数列{an+1}是首项为2,公比为3的等比数列,∴an+1=2·3n-1,因此an=2·3n-1-1.典型的递推数列及处理方法2递推式方法示例an+1=an+f(n)叠加法a1=1,an+1=an+2n=f(n)叠乘法a1=1,=2nan+1=pan+q(p≠0,1,q≠0)化为等比数列a1=1,an+1=2an+1an+1=pan+q·pn+1(p≠0,1,q≠0)化为等差数列a1=1,an+1=3an+3n+1其中(1)an+1=pan+q(p≠0,1,q≠0)的求解方法是设an+1+λ=p(an+λ),即an+1=pan+pλ-λ,与an+1=pan+q比较知只要λ=即可.(2)an+1=pan+q·pn+1(p≠0,1,q≠0)的求解方法是两端同时除以pn+1,即得-=q,数列为等差数列.[变式训练]根据下列条件,确定数列{an}的通项公式:(1)a1=2,an+1=an+3n+2;(2)a1=1,an=an-1(n≥2);(3)a1=1,an+1=2an+1.【解】(1)∵an+1-an=3n+2,∴an-an-1=3n-1(n≥2),∴an=(an-an-1)+(an-1-an-2)+…+(a2-a1)+a1=(n≥2).当n=1时,a1=×(3×1+1)=2适合上式,∴an=n2+.(2)∵an=an-1(n≥2),∴=(n≥2),∴an=··…··a1=··…··1=,当n=1时适合上式,故an=.(3)∵an+1=2an+1,∴an+1+1=2(an+1),又a1=1,∴a1+1=2.∴数列{an+1}是首项为2,公比为2的等比数列.∴an+1=2·2n-1,∴an=2n-1.3