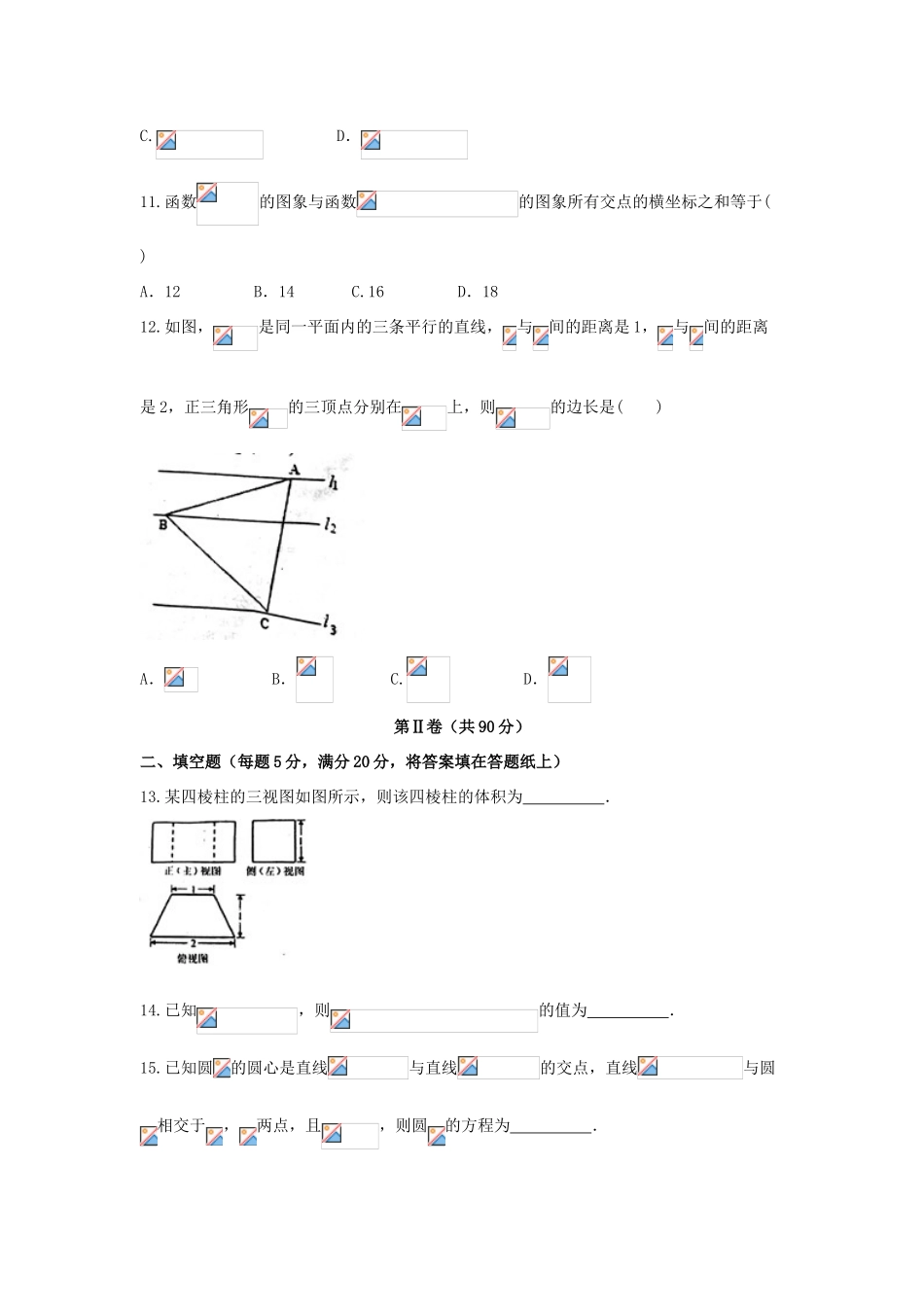
2016-2017学年度高一(下)期末考试数学(理)试题第Ⅰ卷(共60分)一、选择题:本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.在中,已知,则的形状是()A.等腰三角形B.直角三角形C.等腰直角三角形D.等腰三角形或直角三角形2.两个相关变量满足如下关系:2345625●505664根据表格已得回归方程:,表中有一数据模糊不清,请推算该数据是()A.37B.C.39D.3.某单位有老年人27人,中年人54人,青年人81人,为了调查他们的身体状况的某项指标,需从他们中间抽取一个容量为42的样本,则老年人、中年人、青年人分别应抽取的人数是()A.7,11,18B.6,12,18C.6,13,17D.7,14,214.函数的单调递增区间是()A.B.C.D.5.盒中共有形状大小完全相同的5个球,其中有2个红球和3个白球,若从中随机取2个球,则概率为的事件是()A.都不是红球B.恰有1个红球C.至少有1个红球D.至多有1个红球6.如图圆内切于扇形,,若在扇形内任取一点,则该点在圆内的概率为()A.B.C.D.7.在中,分别为三个内角所对的边,设向量,,若,则角的大小为()A.B.C.D.8.下列命题中,假命题是()A.若且,则B.若,则恒成立C.的最小值是D.,9.在中,为的四分之一等分点(靠近点),点在线段上,若,则实数的值为()A.B.C.1D.10.已知圆,圆与圆关于直线对称,则圆的方程为()A.B.C.D.11.函数的图象与函数的图象所有交点的横坐标之和等于()A.12B.14C.16D.1812.如图,是同一平面内的三条平行的直线,与间的距离是1,与间的距离是2,正三角形的三顶点分别在上,则的边长是()A.B.C.D.第Ⅱ卷(共90分)二、填空题(每题5分,满分20分,将答案填在答题纸上)13.某四棱柱的三视图如图所示,则该四棱柱的体积为.14.已知,则的值为.15.已知圆的圆心是直线与直线的交点,直线与圆相交于,两点,且,则圆的方程为.16.等腰的顶角,,以为圆心,1为半径作圆,为该圆的一条直径,则的最大值为.三、解答题(本大题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.)17.已知函数.(1)求的最小正周期;(2)求在区间上的最大值和最小值.18.一个袋中装有四个形状大小完全相同的球,球的编号分别为1,2,3,4.(1)从袋中随机抽取两个球,求取出的球的编号之和不大于4的概率;(2)先从袋中随机取一个球,该球的编号为,将球放回袋中,然后再从袋中随机取一个球,该球的编号为,求的概率.19.在三角形中,角及其对边满足:.(1)求角的大小;(2)求函数的值域.20.在中,分别为角的对边,设.(1)若,且,求角的大小;(2)若,求角的取值范围.21.已知圆,直线.(1)求直线所过定点的坐标;(2)求直线被圆所截得的弦长最短时的值及最短弦长.(3)已知点,在直线上(为圆心),存在定点(异于点),满足:对于圆上任一点,都有为一常数,试求所有满足条件的点的坐标及该常数.22.已知向量,,且向量.(1)求函数的解析式及函数的定义域;(2)若函数,存在,对任意,总存在唯一,使得成立,求实数的取值范围.2016-2017学年度高一(下)期末考试数学(理)试题参考答案一、选择题1-5:DCDBB6-10:CBDAA11、12:AD二、填空题13.14.15.16.三、解答题17.解:(1)因为所以的最小正周期为.(2)因为,所以.于是,当,即时,取得最大值2.当,即时,取得最小值.18.解:(1)从袋中随机取两个球,可能的结果有6种,而取出的球的编号之和不大于4的事件有两个,1和2,1和3,∴取出的球的编号之和不大于4的概率.(2)先从袋中随机取一个球,该球的编号为,将球放回袋中,然后再从袋中随机取一个球,该球的编号为,所有有(种),而有1和3,1和4,2和4三种结果,∴.19.解:(1)由条件得:,所以,,又,所以,,因为,所以,所以,又,所以.(2)在三角形中,,故.因为,所以.所以,.所以,函数的值域为.20.解:(1)由,得,∴,又由正弦定理,得,,将其代入上式,得, ,∴,将其代入上式,得,∴,整理得:,∴. 角是三角形的内角,∴.(2) ,∴,即,由余弦定理,得,∴(当且仅当时取等号).∴,是锐角,又 余弦函数在上递减,∴.21.解:(1)依题意得,,令,且,得,,∴直线过定点.(2)当时,所截得弦长最短,由题知,.∴,得...