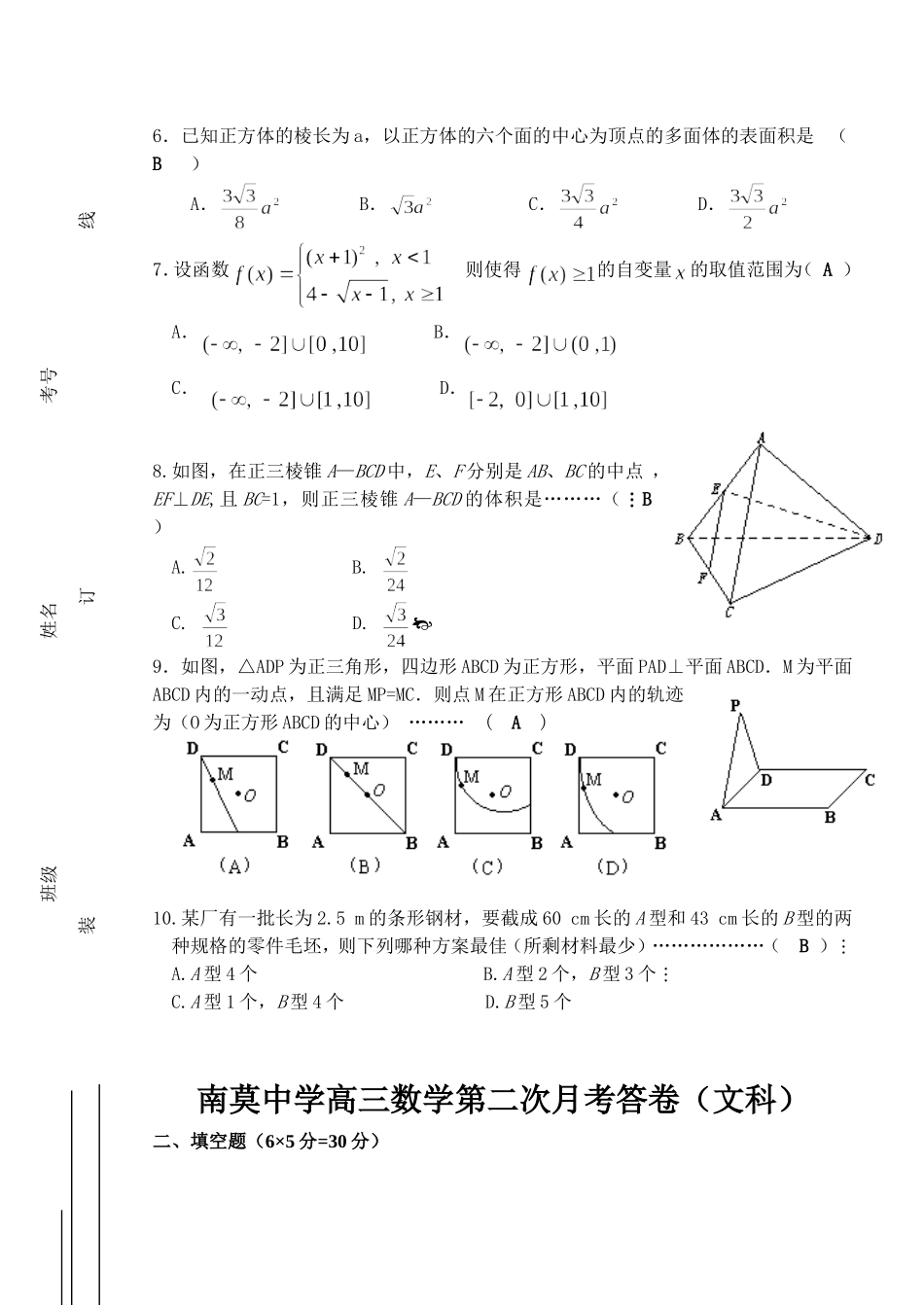
南莫中学高三数学第二次月考试卷(文科)命题人:万金圣2007.10.3一、选择题(10×5分=50分)1.已知集合A,B,I,.则下面关系式正确的是(D)A.(IA)∪(IB)=IB.(IA)∪B=IC.A∪B=ID.(I(A∩B))∪(A∩B)=I2.已知函数,则m等于(B)A.B.-C.D.-3.将函数的图象向右平移个单位后得到函数的图象,则函数的图象关于(C)A.直线对称B.点()对称C.直线对称D.点()对称4.“”是“方程表示椭圆”的(B)A.充分而不必要条件B.必要而不充分条件C.充要条件D.既不充分也不必要条件5.如果直线与圆有两个不同的交点,则点P()与圆C的位置关系是(A)。A.在圆外B.在圆上C.在圆内D.无法判断6.已知正方体的棱长为a,以正方体的六个面的中心为顶点的多面体的表面积是(B)A.B.C.D.7.设函数则使得的自变量的取值范围为(A)A.B.C.D.8.如图,在正三棱锥A—BCD中,E、F分别是AB、BC的中点,EF⊥DE,且BC=1,则正三棱锥A—BCD的体积是………(B)A.B.C.D.9.如图,△ADP为正三角形,四边形ABCD为正方形,平面PAD⊥平面ABCD.M为平面ABCD内的一动点,且满足MP=MC.则点M在正方形ABCD内的轨迹为(O为正方形ABCD的中心)………(A)10.某厂有一批长为2.5m的条形钢材,要截成60cm长的A型和43cm长的B型的两种规格的零件毛坯,则下列哪种方案最佳(所剩材料最少)………………(B)A.A型4个B.A型2个,B型3个C.A型1个,B型4个D.B型5个南莫中学高三数学第二次月考答卷(文科)二、填空题(6×5分=30分)装订线班级姓名考号11.已知A={a,b,c},B={-5,0,5},是A到B的映射,则满足的映射共有7个。12.已知数列{an}的前n项的和,则数列{an}的通项an=____________.13.已知椭圆的两个焦点为F1、F2,过F2作垂直于x轴的直线与椭圆相交,一个交点为P,若∠PF1F2=30°,那么椭圆的离心率是____________.14.在坐标平面上,不等式组所表示的平面区域的面积3/2.15.在算式“1×□+4×□=30”的两个□中,分别填入两个自然数,使它们的倒数之和最小,则这两个数应分别为_10和5_______.16.下面四个命题①过已知直线外一点,与已知直线平行的直线有且只有一条;②过已知直线外一点,与已知直线垂直的直线有且只有一条;③过已知平面外一点,与已知平面平行的直线有且只有一条;④过已知平面外一点,与已知平面垂直的直线有且只有一条;其中命题的序号是①,④..三、解答题(本大题共5小题共70分,解答时应写出文字说明、证明过程或演算步骤)17.(本小题满分12分)已知函数(Ⅰ)求的单调递增区间;(Ⅱ)若不等式都成立,求实数m的最大值.解:(Ⅰ)因为…2分…………………………4分由得所以的单调增区间是……………………6分MEBADCF(Ⅱ)因为所以…8分所以…………………………10分所以的最大值为1.………………………………12分解(1)直线方程为x-y=0……………………………………………………6分(2)r=………………………………………………………………12分19.(本小题满分14分)如图,在梯形中,∥,,.平面平面,四边形是矩形,,点在线段上.(1)求证:平面;(2)当为何值时,∥平面?证明你的结论;(Ⅰ)证明:在梯形ABCD中,,………………………………4分又 平面ACFE⊥平面ABCD,交线为AC,…………………………………6分(Ⅱ)解:当……………………8分在梯形ABCD中,设,连结FN,则CN:NA=1:2。…………………………………………………………11分又………………………………………………14分20.(本小题满分16分)设、,向量,,且(1)求点的轨迹C的方程;(2)过点P(0,2)作直线交曲线C于A、B两点,又O为坐标原点,若,求直线的倾斜角。………………………………6分……………………………………………………………………………………9分………………………………………11分……………………………………………13分……………………………………………16分21.(本小题满分16分)已知函数的图象过点,且方程有两个相等的实数根.(1)求实数的值;(2)若正项数列满足:,求通项;(3)对满足(2)中的数列,若数列,为数列的前项和,证明:.解(1) ...